Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

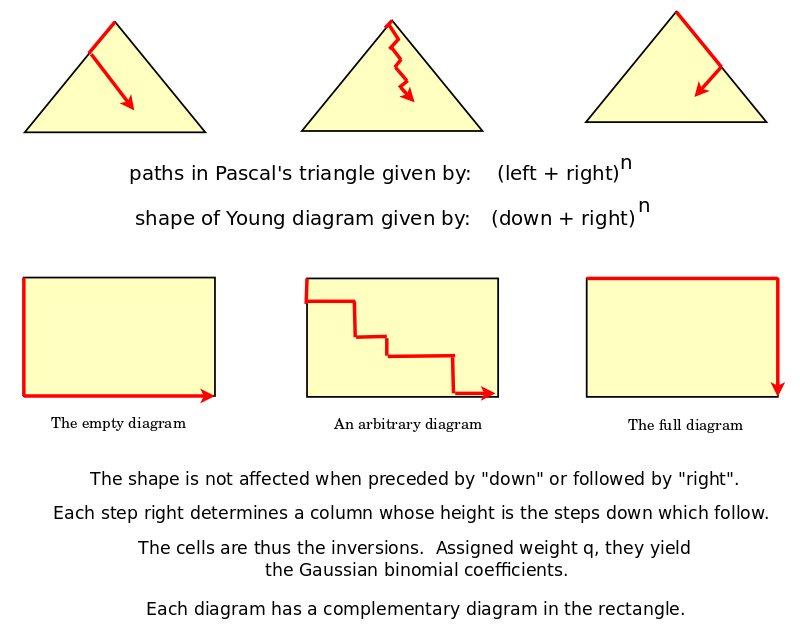
Each location (n i) in Pascal's triangle, where i goes from 0 to n, can be identified with the Young diagrams that fit in a rectangle with sides of length i+1 and n-i+1.

Thus a Young diagram can be identified with a smallest location (n i) and all locations (m j) for which j>=i and m-j >= n-i, which is to say, for all in the triangle below (n i).

Discussion

Note that each cell in the rectangle gives the choice, across terms, of x-choice-left vs. y-choice-right. So we can thus infer choices - how we would have chosen - given the choices available, and given the choices made. Inversions are related to a change in choice, in preference, and thus they provide information about changes in the chooser. Extrinsic vs. intrinsic symmetry issues become relevant.

Given an initial infinite sequence: ...down-down-down-right-right-right... consider the possible (finite) ways that it could be perturbed, for example: ...down-down-down-right-right-down-right-right-right... Such perturbations are the paths, or equivalently, the Young diagrams.