Introduction E9F5FC

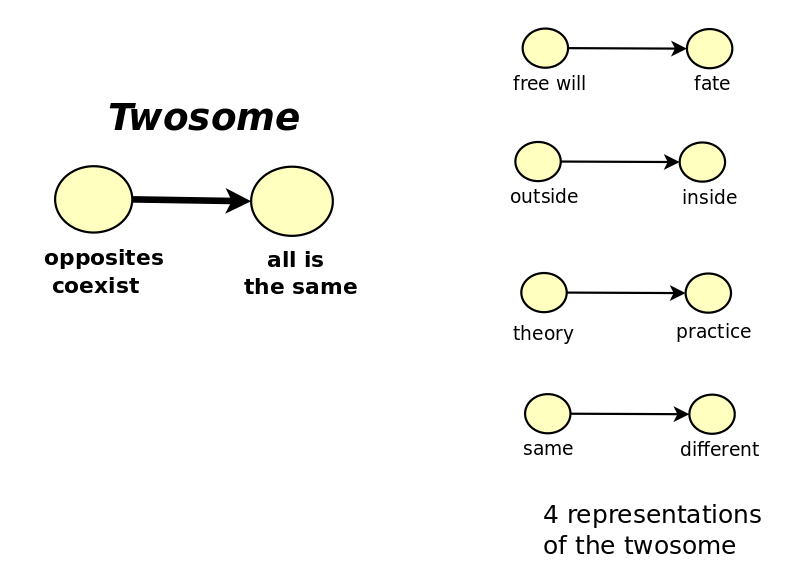
Questions FFFFC0

• View
• Edit
• History
• Print

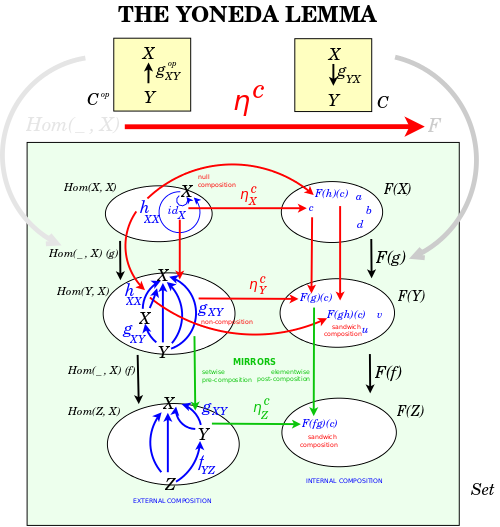
Yoneda lemma, Yoneda Lemma Presentation, Interpreting Yoneda lemma

---

Yoneda Lemma as a Knowledge Switch

An Outsider's Understanding of Category Theory as Metaphor Theory

---

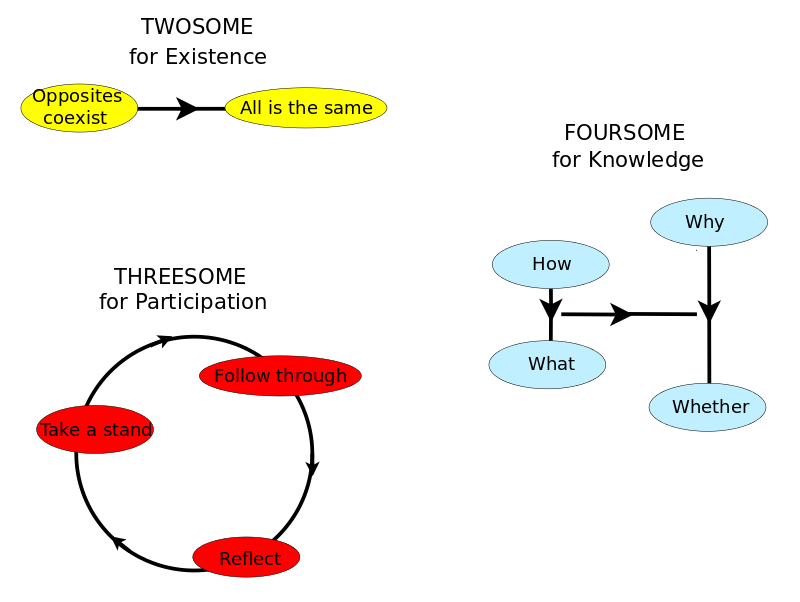
Four Levels of Knowledge: Whether, What, How, Why

---

---

---

---

---

---

---

---

---

---

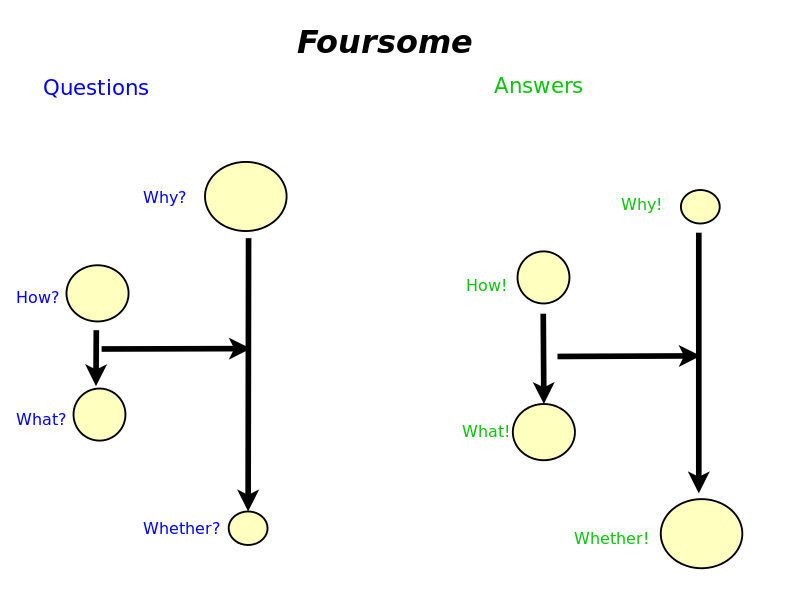
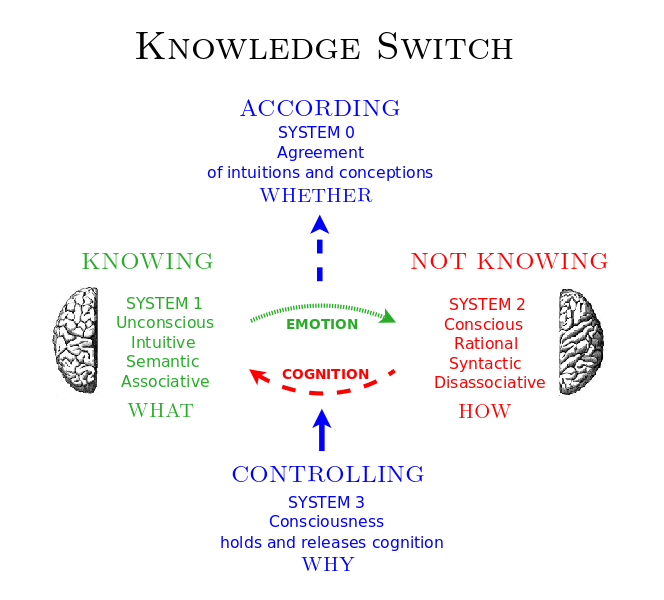
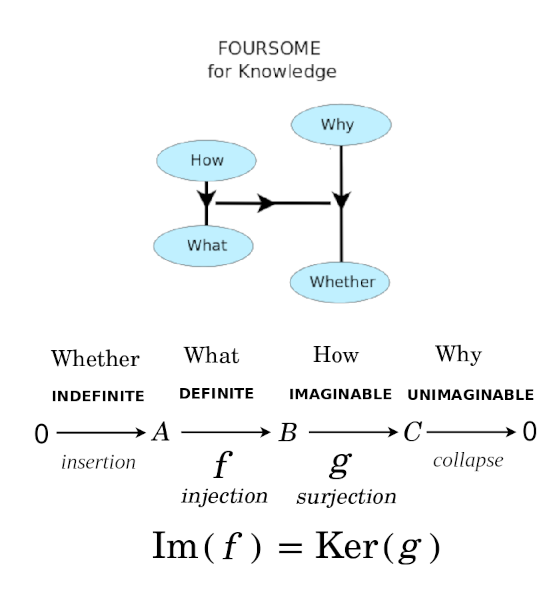
Whether, What, How, Why

• Whether: Identity morphism (distinguished arrow of sameness of object) - Yoneda-y principle (Cheng)
• What: Fa - "functor as picture" (Awodey)
• How: {$a\rightarrow x$} "functor as construction" (Awodey)
• Why: {$\forall x[a\rightarrow x]$} (all possible arrows to all possible objects) - Yoneda perspective (Bradley)

Steve Adowey "Category Theory Foundations, Lecture 3", 25:30. "A functor is a picture of one category in another category. It takes all of the objects and arrows in one category and gives you an image of them over in the other category, maintaining all of the relations of mappability between the objects and even the relations of composition of mappings and so on." "And the functor G gives another picture of that category. ... A natural transformation consists of a family of maps k

27:45 [Rough notes] A good way is as a kind of construction on the objects in the category C. You use them to construct something over in category D. But it's some sort of abstract construction. Theta is a way of transforming one of the constructions into the other. It relates the whole construction F to the whole construction G.

---

---

Yoneda Lemma explanation

{$\forall x [(a\rightarrow x)\rightarrow Fx] \cong Fa$}

Given the knowledge {$Fa$} and understanding that {$F$} is a functor, we are able, for any {$x$}, given a morphism {$a\rightarrow x$}, to produce the value {$Fx$}. This is because a functor {$F$} translates the morphism {$a\rightarrow x$} into the morphism {$Fa\rightarrow Fx$}, and given {$Fa$} we can get {$Fx$}. So the functor {$F$} contains the missing information.

Given a natural transformation of the form {$\forall x [(a\rightarrow x)\rightarrow Fx]$} we can set {$x=a$} and then we have that {$a\rightarrow a$} yields {$Fa$}.

State this more exactly.

Show that these are inverses of each other.

---

Element of a Set

Yoneda lemma explains what is an element of a set (the internal view) in terms of natural transformations (the external view).

One way of looking is as the elements of a set.

Another way of looking is as natural transformations.

---

Natural isomorphism

A natural isomorphism is two different but compatible ways of looking at the same world.

Given an arrow between objects in the world, there are two functors that present that arrow, and there exist component maps for each object so that the functors commute. The component maps exist in either direction.

---

Natural isomorphism of bifunctors

The Yoneda lemma works with bifunctors. Thus the world is the product {$C\times\textrm{Set}^{C^{op}}$}. The functors are defined on objects that pair an object in {$C$} and a functor from {$C^{op}$} to {$\textrm{Set}$}.

There is something special about isolating an object c in C, just as there is something special as having a functor from C into Set. And those two special things are balanced.

The Yoneda Lemma identifies the view of "isolation" with the view of "nonisolation"

{$Fc$} has us consider the functor F acting on the object c, thus yielding an output set. And in doing so it is giving an image of all of the relationships in C with that object, and through composition, with further morphisms and objects, and lifting that up to the world of sets. Furthermore, we seem to be taking the functor F in isolation but actually it exists amongst all of its own relationships.

{$\textrm{Hom}(\textrm{Hom}(c,\_),F)$} takes as input the functor F and the object c. It yields the set of natural transformations {$\{\psi^u | u\in F(c)\}$} where {$\psi^u_c(\textrm{id}_c)=u$}. This set is determined by the set {$F(c)$}. And it is all the set of all of the natural transformations from this functor Hom(c,_) to the functor F.

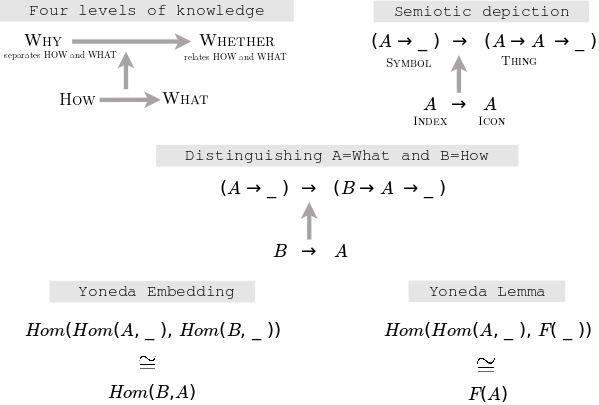
Given c and F we can define levels of knowledge

• How {$F:x\rightarrow F(x)$} and, in particular, {$x=c$}
• What {$F(c)$} the whole set, which lives in the world of sets
• Why {$\{F(f)\; |\; x\in C, f\in \textrm{Hom}(c,x)\}$}
• Whether {$u\in F(c)$}, an element in the set which, by way of the associated natural transformation {$\psi^u$}, is identified with the identity {$u=\psi^u(\textrm{id}_c)$}

These levels carry the same information but in different contexts, with different levels of explicitness. It may seem that {$F(c)$} has lost information but in fact its elements correspond to the natural transformations and allow us to compute them. These elements are the aspects and any one of them can be taken as the essence of existence, of "whether" that is established by the corresponding natural transformation. Note also that we can hold c and F fixed or we can change them across all objects and morphisms in C and all functors and natural transformations in C->Set.

So this is about the identification {$u \Leftrightarrow \psi^u$} where {$u\in F(c)$} and {$\psi^u \in \textrm{Hom}(\textrm{Hom}(c,\_),F)$}.

Given {$\psi^u$} we can calculate {$u=\psi^u_c(\textrm{id}_c)$}.

Given {$u$} we can set {$u=\psi^u_c(\textrm{id}_c)$}. Then what is {$\psi^u_x:\textrm{Hom}(c,x)\rightarrow F(x)$}? Specifically, for {$f\in\textrm{Hom}(c,x)$}, what is {$\psi^u_x(f)$}? We set {$\psi^u_x(f)=F(f)(u)$}. Which is to say, the morphism {$f:c\rightarrow x$} in the set {$\textrm{Hom}(c,x)$} is mapped to the element {$F(f)(u)\in F(x)$}. Note that we had {$u\in F(c)$}. So the morphism {$f$} is mapped to the element that {$F(f)$} takes us to starting from {$u$}. Which means that {$F(f)$} is providing us with initial state {$u\in F(c)$} and terminal state {$F(f)(u)\in F(x)$}. Whereas we started with a morphism {$f$}.

---

Identifications

With the Yoneda lemma we identify

	Sets (objects in the category Set)
{$F(c)$}	{$\Leftrightarrow$}	{$\textrm{Hom}(\textrm{Hom}(c,\_),F)$}
	Set members
{$u$}	{$\Leftrightarrow$}	{$\psi^u$}
	Set members (described more explicitly)
{$F:c\rightarrow F(c)\ni u$}	{$\Leftrightarrow$}	{$\psi^u:\textrm{Hom}(c,\_)\rightarrow F$}
	Set membership in terms of interpretations (functors of type {$C\rightarrow \textrm{Set}$})
{$u$} is one state within the interpretation {$F(c)$} of {$c$}	{$\Leftrightarrow$}	{$\psi^u$} is one path from the interpretation {$\textrm{Hom}(c,x)$} of {$x$} in terms of relationships with {$c$} to the interpretation {$F(x)$}
	Interpretation restricted to relationships with {$x$} as given by {$F:[c\overset{f}{\rightarrow} x]\rightarrow [F(c)\overset{F(f)}{\rightarrow} F(x)]$}
the interpretation {$F(f)$} of relationship {$f$} (as a set function) has (input) initial state {$u$} thus {$F(f):u\rightarrow F(f)(u)$}	{$\Leftrightarrow$}	component (interpreting {$x$}) {$\psi^u_x:\textrm{Hom}(c,x)\rightarrow F(x)$} is a set function mapping relationship {$c\overset{f}{\rightarrow}x$} to some terminal state in {$F(x)$}
	Interrelation in terms of {$f:c\rightarrow x \in \textrm{Hom}(c,\_)$}
{$u=\psi^u_c(\textrm{id}_c)$} arising by setting input {$f$} to the do-nothing action {$c\overset{\textrm{id}_c}{\rightarrow}c$}	{$\Leftrightarrow$}	{$\psi^u_x(f)=F(f)(u)$} for all {$f$}
	Algorithm
{$u$} is the initial state which is also a terminal state by virtue of applying {$\psi^u_c$} to the do-nothing action {$\textrm{id}_c$}	{$\Leftrightarrow$}	Given {$c\overset{f}{\rightarrow}x$}, {$\psi^u_x$} uses {$F$} to apply {$F(f)$} to initial state {$u$} and yields terminal state {$\psi^u_x(f)=F(f)u$}
	Overall action on {$c\overset{f}{\rightarrow}x$}
{$c\overset{f}{\rightarrow} x$} is interpreted as {$F(c)\overset{F(f)}{\rightarrow}F(x)$} within which we have {$u\overset{F(f)}{\rightarrow}{F(f)u}$}	{$\Leftrightarrow$}	{$\psi^u_x$} takes {$f$} and uses {$u\overset{F(f)} {\rightarrow}{F(f)u}$} to go from initial state {$u$} to terminal state {${F(f)u}$} which it returns
	Overall action on {$a\overset{f}{\rightarrow}b$} and {$F\overset{\alpha}{\rightarrow}G$} yielding set functions {$S,T:F(a)\rightarrow G(b)$}

---

Natural transformation

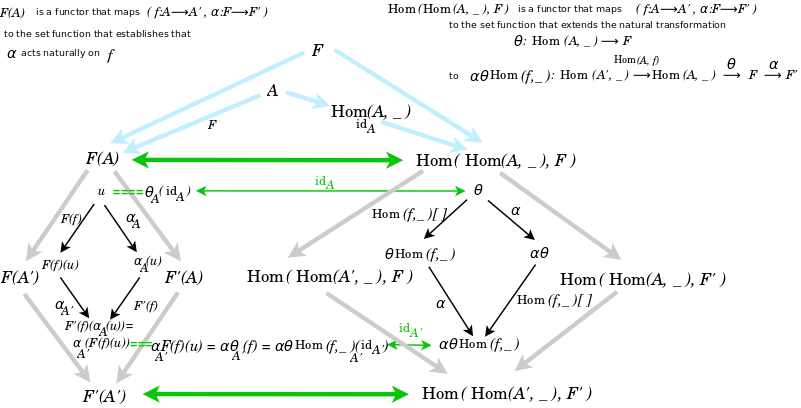
We are given two functors {$L$} and {$R$} from {$C\times\textrm{Set}^C$} to {$\textrm{Set}$}.

A natural transformation {$\eta$} from {$L$} to {$R$} associates to every object {$(A,F)$} a set function {$\eta_{(A,F)}:L((A,F))\rightarrow R((A,F))$}. Specifically, this sends {$u$} to {$\psi^u$}. Components satisfy the commutative diagram by which for every {$(f,\alpha):(A,F)\rightarrow (A',F')$} we have {$\eta_{(A',F')}\circ L((f,\alpha))=R((f,\alpha))\circ \eta_{(A,F)}$}.

And for this to be a natural isomorphism we furthermore need that each component {$\eta_{(A,F)}$} is an isomorphism in {$\textrm{Set}$}.

An isomorphism is a morphism, and in our case, a set function {$u\overset{m}{\rightarrow}v$} for which there is a morphism {$v\overset{m^{-1}}{\rightarrow}u$} such that {$m^{-1}m=1_u$} and {$mm^{-1}=1_v$}.

Applying to get the Yoneda Lemma

A natural transformation {$\eta$} from {$L=F(A)$} to {$R=\textrm{Hom}(\textrm{Hom}(A,\_),F)$} associates to every object {$(A,F)$} a set function {$\eta_{(A,F)}:F(A)\rightarrow \textrm{Hom}(\textrm{Hom}(A,\_),F)$}. Specifically, the set function is {$\eta_{(A,F)}:u\rightarrow\psi^u$}. Components satisfy the commutative diagram by which for every {$(f,\alpha):(A,F)\rightarrow (A',F')$} we have {$\eta_{(A',F')}\circ L((f,\alpha))=R((f,\alpha))\circ \eta_{(A,F)}$}.

{$L((f,\alpha))$} is the set function which sends {$u\in F(A)$} to {$u'\in F'(A')$} where {$u'=F(f)(\alpha_A(u))=\alpha_{A'}(F(f)(u))$}

{$R((f,\alpha))$} is the set function which sends {$\psi^u\in \textrm{Hom}(\textrm{Hom}(A,\_),F)$} to {$\hat{\psi}^{u}\in \textrm{Hom}(\textrm{Hom}(A',\_),F')$} where {$\hat{\psi}^{u}=\alpha\psi^{u}\textrm{Hom}(f,\_)$} Note that {$\textrm{Hom}(f,\_)$} is the natural transformation which prepends {$f:A\rightarrow A'$}. Then we can apply {$\psi^u$}. And then we can apply {$\alpha:F\rightarrow F'$}.

Components satisfy the commutative diagram by which for every {$(f,\alpha):(A,F)\rightarrow (A',F')$} we have for {$u\in F(A)$}

{$\eta_{(A',F')}\circ L((f,\alpha))(u)=\eta_{(A',F')}(u')=\psi^{u'}$}

And we have {$=R((f,\alpha))\circ \eta_{(A,F)}(u) = R((f,\alpha))(\psi^{u}) = \hat{\psi}^u = \alpha\psi^u \textrm{Hom}(f,\_)$}.

Thus we need to check whether {$\psi^{u'}=\alpha\psi^u \textrm{Hom}(f,\_)$} are the same as natural transformations from the functor {$\textrm{Hom}(A',\_)$} to the functor {$F'$}, where both functors are from {$C$} into {$\textrm{Set}$}.

Note that {$\textrm{Hom}(f,\_)$} is a natural transformation from the functor {$\textrm{Hom}(A',\_)$} to the functor {$\textrm{Hom}(A,\_)$} which works by prepending the morphism {$f:A:\rightarrow A'$}. The component {$\textrm{Hom}(f,\_)_X$} takes a morphism {$g\in\textrm{Hom}(A',X)$} to the morphism {$g\circ f\in\textrm{Hom}(A,X)$}.

We have to check that for any particular component {$X$} in {$C$} these natural transformations give the same result as set functions. As set functions their components take an input in {$\textrm{Hom}(A',X)$} of the form {$g:A'\rightarrow x$} and we need to show that they give the same result on {$g$}.

Thus we ask whether {$\psi^{u'}_X(g)$} equals {$\hat{\psi}^u_X(g)$}?

Note that {$u'\in F'(A')$} and {$\psi^{u'}:\textrm{Hom}(A',\_)\rightarrow F'$} by definition. Also, {$\psi^u_X(f)=F(f)u$} for {$f:A\rightarrow X$} and likewise {$\psi^{u'}_X(g)=F'(g)u'$} for {$g:A'\rightarrow X$}.

{$\psi^{u'}_X(g)=F'(g)(u')=F'(g)(\alpha_{A'}(F(f)(u))$}

{$=F'(g)(F'(f)(u))=F'(g\circ f)(u)= \alpha_X (F(g\circ f)(u)) = \alpha_X \psi^u_X(g\circ f)=\alpha_X\psi^u_X\textrm{Hom}(f,\_)_X(g) = (\alpha\circ\psi^u\circ\textrm{Hom}(f,\_))_X(g) $}

---

Interpretation

The Imposition, which is to say, cognition. The opposite would be the Contradiction, which is to say, emotion.

We cannot distinguish with {$\alpha$} between F and F' to establish Whether unless we first distinguish with {$\textrm{Hom}(f,\_)$} to establish Why. How F,A leads to What F(A). And this is what is needed so that Why {$\textrm{Hom}(f,\_)$} can lead to Whether {$\alpha$}. In between the conscious and the unconscious, in between God beyond and God within, are we - the subject of knowledge, the boundary, which is ever developed by the chain complexes / exact sequences.

The natural transformation {$\psi^u$} expresses the soft-wired conscious set world in terms of the hard-wired unconscious set world. It is an interface. The Yoneda Lemma takes us from the intrinsic interface based on X to a more extrinsic, implicit interface based on A - X - A', which makes objects explicit as initial and terminal states. We develop external memory.

---

---

---

---

The germ of the Yoneda Lemma

The Yoneda Lemma generalizes the fact that the following two statements are equivalent:

1) You can keep up with me.

2) Take anybody, if I can keep up with them, then you can keep up with them, too.

Suppose 1). If I can keep up with somebody, then since you can keep up with me, it follows that you can keep up with them. This gives 2).

Suppose 2). Note that I can keep up with myself. Thus you can keep up with me. This gives 1).

We may term these the direct formulation 1) and the universal formulation 2).

---

A fact about preorders

Let's write this out mathematically.

A preorder is a binary relation that is reflexive {$a\leq a$} and transitive {$a\leq b \wedge b\leq c \Rightarrow a\leq c$}. An example is the natural numbers.

The Yoneda Lemma is a generalization of the following fact about preorders.

{$y\leq x$} iff {$(\forall z)(z\leq y \Rightarrow z\leq x)$}

From left to right, we use transitivity: If {$y\leq x$} and {$z\leq y$}, then {$z\leq x$}.

From right to left, we instantiate {$z$} to {$y$}, and use reflexivity: {$y\leq y$}, thus {$x\leq y$}.

Thus we have two ways of looking at the same fact. We may focus on the particular relation between {$x$} and {$y$}, or we can consider the general correlation in their relationships with every {$z$}.

Transitivity takes us from the particular relation to the general correlation. Instantiation and reflexivity take us from the general correlation to the particular relation.

Note that it is crucial for reflexivity that the relation be weakly increasing and not strictly increasing. This distinction is critical for the Yoneda lemma because it leverages reflexivity.

Preliminaries

---

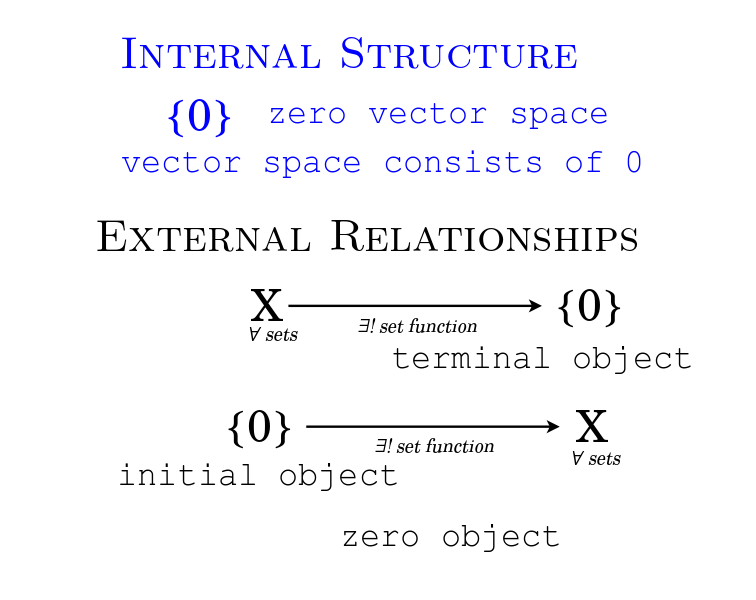
Describing Facts in a World: External Relationships vs. Internal Structure

---

---

---

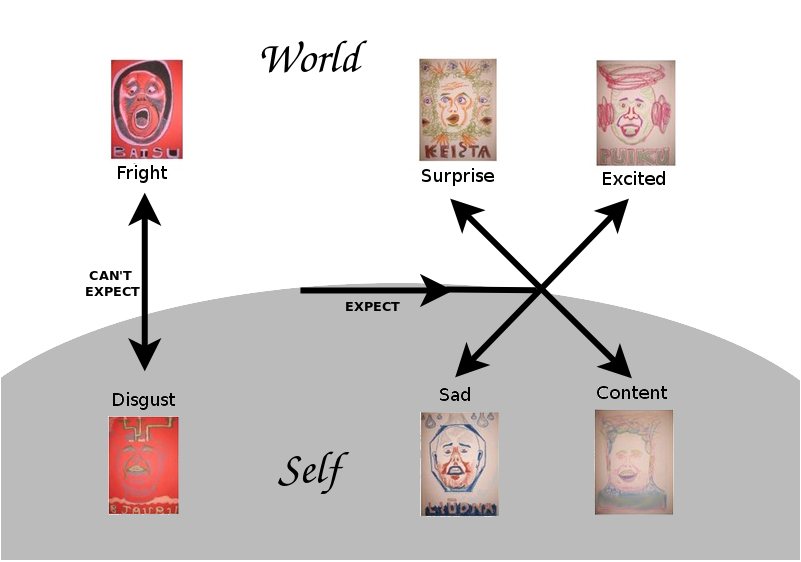
Emotionally: Beauty vs. Intimacy

---

---

---

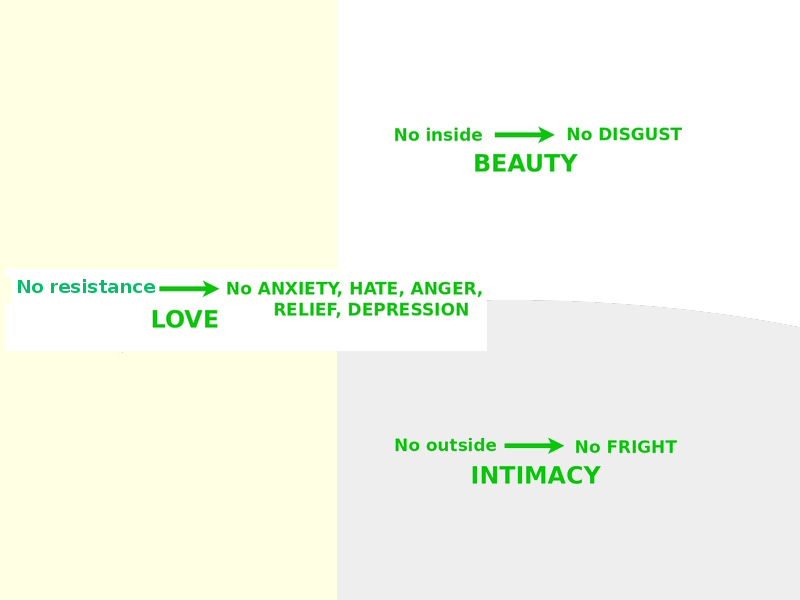
Limits Describe External Relationships, Colimits Describe Internal Structure

---

Metaphor (Between Worlds) as Adjunction

Vector space and Set - Forgetful (Right) and Free (Left)

{$L\dashv R$} where {$\mathcal{D}\begin{matrix}\overset{L}{\longrightarrow} \\ \bot \\ \underset{R}{\longleftarrow} \end{matrix} \mathcal{C}$}

counit {$\eta : 1_{\mathcal D} \to RL$} In what sense is this relaxing interpretation? Draw the commutative diagram.

unit {$\varepsilon : LR \to 1_{\mathcal C}$} In what sense is this restricting interpretation? Draw the commutative diagram.

{$R\xrightarrow{\;\eta R\;}RLR\xrightarrow{\;R \varepsilon\,}R$}

{$L\xrightarrow{\;L\eta\;}LRL\xrightarrow{\;\varepsilon L\,}L$}

---

Classifying adjunctions

---

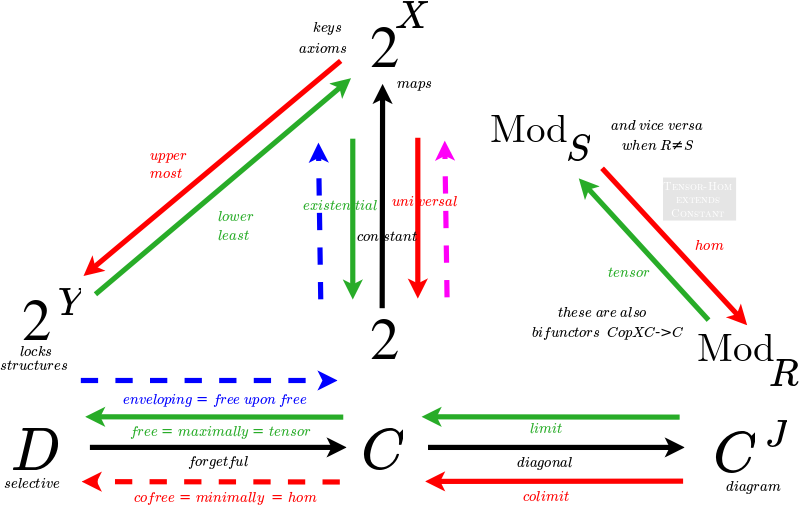
Natural Transformation as a type of Adjunction

Definition

---

Yoneda Embedding

{$\textrm{Set}(C(A,\_),C(B,\_))\cong C(B,A)$}

{$\forall X.C(A,X)\rightarrow C(B,X)\cong C(B,A)$}

This means that the only way to have a natural transformation on the left hand side is for it to add an arrow {$B\overset{f}{\rightarrow} A$} to {$C(A,\_)$}.

We can see this by considering the case when {$X=A$}.

Awodey 48:30

{$Hom(C,D)\cong Hom(yC,yD)$} by the Yoneda lemma where y is the Yoneda Embedding and yD=F

{$\textrm{Set}^{C^{op}}$} is nice because it is Cartesian closed, it has natural numbers as a functor, thus inductively defined types, it has sigmas and pis, it is a topos, it has higher order logic, it has interpretation of all of propositional, first order and second order logic, it has cohomology theory. Can use the polymorphic lambda calculus. Can reflect back down the maps we construct and prove in the nice world.

---

Yoneda Embedding Consequence: Indirect Equality

{$A\cong B \Leftrightarrow \forall X[C(A,X)\cong C(B,X)]$}

---

Representable functor

A functor {$F : C → \textrm{Set}$} is said to be representable if it is naturally isomorphic to {$\textrm{Hom}(A,–)$} for some object {$A$} of {$C$}.

A representation of {$F$} is a pair {$(A, Φ)$} where {$ Φ : Hom(A,–) \rightarrow F $} is a natural isomorphism.

Examples

Our functor takes an object B to the set of all functions from B to A.

Richard Borcherds 2:10. {$\mathcal{C}=\mathbf{Top}$} Topological spaces. {$A=\mathbb{R}$}. {$h_A(B)=C(B)$} continuous real functions on {$B$}.

What is it for the Grassmannian?

---

Interpretation As Knowledge Switch

---

Identity Map is the Do Nothing Action

The Do-nothing-action is "theory" (off) as opposed to "practice" (on).

---

Yoneda Perspective

Holography

---

Examples

---

Cayley's theorem

---

Category of matrices

• Explained by Emily Riehl
• C is the category whose arrows are {$n\times m$} matrices over a field {$K$} and whose objects are the natural numbers {$n\geq 0$}.
• the functor {$h_k(n)$} sends a {$m\times n$} matrix to the set of {$n\times k$} matrices
• Problem: understand all column operations that naturally transform (sets of) matrices with k columns into (sets of) matrices with j columns
• Yoneda lemma says that every such column operation is determined by a single {$k\times j$} matrix which is obtained by applying that column operation to the identity matrix {$I_k:k\rightarrow k$}. The column operation is defined by right multiplication by that matrix {$\alpha_k(I_k):k\rightarrow k$}
• Associativity of matrices means that the naturality on the left and multiplication on the right commute.
• Corollary: Column operation is invertible iff the matrix {$\alpha_k(I_k) is invertible.

---

Functor of points

• nLab: functorial geometry
• Functor represented by a scheme
• Math Stack Exchange. Functor of points and category theory.
• Richard E. Borcherds. Schemes 13: The functor of points
• John Huerta. The Functor of Points approach to Supermanifolds.
• Twitter. John Huerta. The functor of points approach.

---

More general forms

---

Kan extension

---

Applications

Type theory

Emily Pillmore: Type Arithmetic and the Yoneda Lemma

---

Related concepts

---

Presheaf

A contravariant functor {$G$} from {$C$} to {$\textrm{Set}$} is the same thing as a functor {$G : C^{op}\rightarrow\textrm{Set}$} and is commonly called a presheaf.

A presheaf is representable when it is naturally isomorphic to the contravariant hom-functor {$\textrm{Hom}(–,A)$} for some object {$A$} of {$C$}.

---

Double Yoneda Embedding

{$C(A,B)\cong \forall F:[C,\textrm{Set}].F(A)\rightarrow F(B)$}

{$a\rightarrow b \cong \forall f.\textrm{Functor} f\Rightarrow fa\rightarrow fb$}

This comes from

{$C(A,B)\cong [C,Set](C(B,\_),C(A,\_)) \cong \forall H.[C,Set](C(A,\_),H)\rightarrow [C,Set](C(B,_),H))$}

---

Profunctors and optics

---

Free cocompletion

nLab: free cocompletion

---

Adjunction

Hom functor outputs values in Set, whereas Internal Hom outputs values in the category C. They both take inputs from Cop×C. A category with Internal Hom is called a closed category. They are closely related to the Yoneda lemma. Examples include cartesian closed categories (Set, or any topos), compact closed categories (notably finite dimensional vector spaces FdVect), monoidal closed categories.

The tensor-curry adjunction relates all and one, as between everything and anything, and between nothing and something. It allows for step-by-step algebra, as by the Yoneda lemma.

Paul Garrett. Adjoints, naturality, exactness, small Yoneda lemma The proof that left adjoints are right-exact, and that right adjoints are left-exact, uses a small incarnation of Yoneda’s Lemma, and illustrates the importance of naturality of isomorphisms.

Riehl page 115: The universal property of the free vector space functor k[−]:Set→Vectk is expressed by saying that it is left adjoint to the underlying set functor U:Vectk→Set: linear maps k[S]→V correspond naturally to functions S→U(V), which specify the image of the basis vectors S⊂k[S]. By the Yoneda lemma, this universal property can be used to define the action of the free vector space functor k[−] on maps. The forgetful functor U:Vectk→Set has no right adjoint, so in this setting there are no competing notions of free construction.

Ext functor is related to the Yoneda product

There is an adjoint 5-tuple between [Setop,Set] and Set. Indeed, given a locally small category B, and the Yoneda embedding, Y:B→[Bop,Set], then Y being the rightmost functor of an adjoint 5-tuple entails that B is equivalent to Set

---

Adjoint string

---

Isbell duality

---

Universality

Random matrices

---

References

---

Videos

ACT 2020 Tutorial: The Yoneda lemma in the category of matrices (Emily Riehl)

27 Unhelpful Facts About Category Theory

A Sensible Introduction to Category Theory

---

Books

Peter Smith. Category Theory: Notes towards a gentle introduction

---

Articles

Barry Mazur. When is one thing equal to some other thing?

Emily Riehl: You never quite understand it.

Eugenia Cheng: If it walks like a duck, talks like a duck and other ducks think it's a duck... then it's a duck.

What do you really need to know in order to make something happen?

Tai-Danae: Yoneda Lemma tells you how to care about things, how to study them. It points you.

Chenchen Song. Category Theory Notes 14: Yoneda Lemma (Part 1)

Chenchen Song. Category Theory Notes 15: Yoneda Lemma (Part 2)

Chenchen Song. Category Theory Notes 16: Yoneda Lemma (Part 3)

Notes

Isomorphism is emulation.

Yoneda Lemma - in what sense is 0, in a short exact sequence, the do nothing action - what is the status of it?

hxameer https://mathstodon.xyz/@xameer/110028561739702961 Yoneda lemma says tells you how to construct, for any a:A, a fibrewise transformation between the hom-functor, (λx.x=a):A→U and another functor P:A→U. Such a transformation has the type ∏x:Ax=a→P(x). It says that to construct this transformation, you just need to construct P(a), and the transformation that you get satisfies certain naturality conditions. This is essentially path induction Egbert Rilke. A type theoretical Yoneda lemma.

Emily Riehl: In Chapter 2, we study such definitions abstractly. A characterization of the morphisms either to or from a fixed object describes its universal property; the cases of “to” or “from” are dual. By the Yoneda lemma—which, despite its innocuous statement, is arguably the most important result in category theory—every object is characterized by either of its universal properties. For example, the Sierpinski space is characterized as a topological space by the property that continuous functions X → S correspond naturally to open subsets of X. The complete graph on n vertices is characterized by the property that graph homomorphisms G → Kn correspond to n-colorings of the vertices of the graph G with the property that adjacent vertices are assigned distinct colors. The polynomial ring Z[x1, . . . , xn] is characterized as a commutative unital ring by the property that ring homomorphisms Z[x1, . . . , xn] → R correspond to n-tuples of elements (r1, . . . ,rn) ∈ R. Modern algebraic geometry begins from the observation that a commutative ring can be identified with the functor that it represents. The idea of probing a fixed object using morphisms abutting to it from other objects in the category gives rise to a notion of “generalized elements” (see Remark 3.4.15). The elements of a set A are in bijection with functions ∗ → A with domain a singleton set; a generalized element of A is a morphism X → A with generic domain. In the category of directed graphs, a parallel pair of graph homomorphisms φ, ψ: A ⇒ B can be distinguished by considering generalized elements of A whose domain is the free-living vertex or the free-living directed edge.8 A related idea leads to the representation of a topological space via its singular complex. The Yoneda lemma implies that a general mathematical object can be represented as a functor valued in the category of sets. A related classical antecedent is a result that comforted those who were troubled by the abstract definition of a group: namely that any group is isomorphic to a subgroup of a permutation group (see Corollary 2.2.10). A deep consequence of these functorial representations is that proofs that general categoricallydescribed constructions are isomorphic reduce to the construction of a bijection between their set-theoretical analogs (for instance, see the proof of Theorem 3.4.12).