Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

I am investigating the different ways that we think of variables. I expect there to be six different ways given by pairs of four levels.

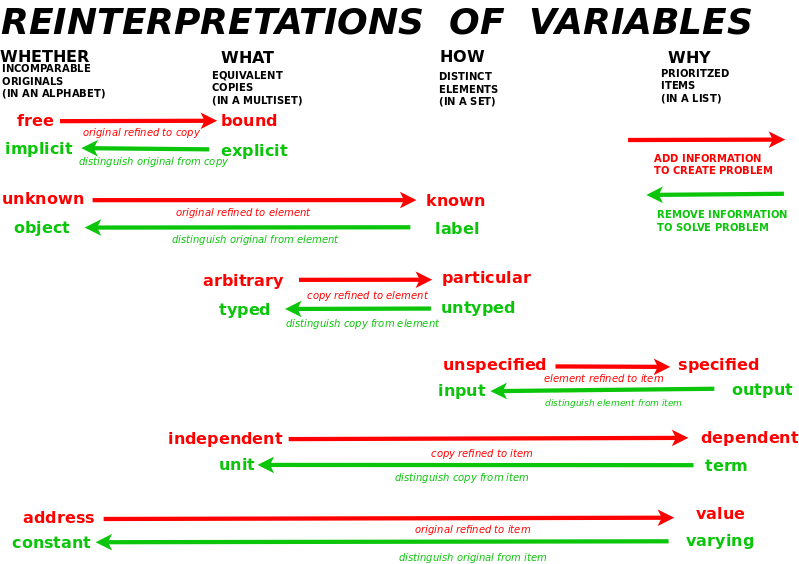
Six types of variables give the ways that visualizations lose information as they restructure. Thus visualizations solve problems. How to make sense of the following?

• Evolution: Given a hierarchy, a sequence distinguishes originals (implicit) among copies (explicit)(in time).
• Atlas: Given a network, a hierarchy distinguishes originals (objects) among a set (of labels).
• Canon: Given a sequence, a network distinguishes copies (of typed) within a set (of untyped).
• Chronicle: Given a sequence, a hierarchy distinguishes distinct elements (inputs) within a list (outputs).
• Catalog: Given a tree, a network distinguishes copies (unit) within a list (of terms).
• Tour: Given a network, a sequence distinguishes originals (constants) from a list (of varying).

Theory

Ideas about variables

• Each variable represents a potential change in state. I expect there to be four possible states. They are the kinds of signs: thing, icon, index, symbol.
• Each variable includes a label and a value. They can be variously related.
• We can organize variable types in terms of explicitness.
• True:
• Direct:
• Constant:
• Significiant:

Pairs of signs:

Examples

Explicit, Implicit

• As in partial differentiation.
• Explicitly indicated.

Free, Bound (Dummy)

• Those without commitments, not already used by logical expressions.
• Those not referred to elsewhere.

Dependent, Independent

• Explicitly a function of another variable, or not.
• May not be explicitly written, though. The relationship may be in our minds.

Random

Arbitrary, Particular

• A member of a set, unspecified or specified
• For all vs. There exists

Varying, Constant

• Fixed variables
• Parameter: An input which remains constant in solving a particular problem

Input (or argument), Output, Evaluated, unevaluated

• What is available as an input for further calculation

Name or label, and what is labelled

• To name a dimension, axis, direction, object

Index, Value

• Used in summation, sequences
• Address (in memory)
• Name of a storage location where some value is kept
• Reference cell that a spreadsheet formula refers to, where a value is kept or described.

Character

• An atom for strings, words.
• The form of the letter or symbol may change slightly, with the font yielding particular connotations or specific meanings, as with math symbols.

Indeterminate (Placeholder), Coefficient

• Unit and amount
• Indeterminate stands for itself, not anything else
  • x in a polynomial or formal power series
  • a letter in an alphabet, in a string
• Indicates our intention, do we intend to solve for it.

Knowns, Unknowns, Constants, Solutions

• We solve for an unknown in terms of knowns.
• Solving a system of linear equations we have unknowns, some or all of which can become knowns. We also have constants.
• Solution: What will become known

Typed, untyped

• Taken to be an instance, a member a of a well-defined "set" or not.
• Declared variable

Assigned variable

• A variable may be declared but only later get assigned a value.

• Center: self-repeating (activity) - keeps finding a center within the center. Thus it defines a "thought", concept, object, item, etc., that which is self-referential, which sustains attention.
• Copies: the act of copying determines a tree, for there are first level copies, copies of copies, and so on.
• Set: defines a network because all elements are distinct with regard to each other, thus also defines a category
• List: order a set sequentially, thus a total order upon it. Is, essentially, counting.
• Equality (of categories) is related to the use of variables (and their meaning).
• A variable is an "atom" of meaning as in my paper, The Algebra of Copyright, which can be parsed on three different levels, yielding four levels and six pairs of levels.

Examples of the use of variables

• A function Phi may be based on an point in the manifold whereas its coordinates may be based on a particular, explicit, specific chart. See Penrose page 186.
• Partial derivative - formal (explicit) based on change in variable, total derivative - actual (implicit) based on change in value.

Notes

• Variables are where the direction is reversed as regards the four relationships between level and metalevel. Variables are, on the one hand, the conclusion of math's "brain", but on the other hand, they are the start of math's "mind".
• Organic variation, variables.
• Homogeneous coordinates are what let us go between a simplex (when Z=1) and the coordinate system (when Z is free). Compare with the kinds of variables.
• With formula we have variables of certain types. And if we have another formula, then we may take all of the variables to be different, but we may allow some of the variables to be the same (refer to the same value) if they have the same type. But in the case of metaphor we see what happens if we make the identification without respecting the type. How much logic can carry over? We can test the boundaries and explore.