Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

Goals

I want to understand the Yoneda lemma and the related category theory so as to mathematically model the concepts of Whether, What, How, Why.

I want to relate the Yoneda lemma to computability theory, especially the jump hierarchy and the Yates index set theorem (which I think basically says that the third jump has complete knowledge of the zeroth jump).

The Fundamental Theorem of Computation

The Yoneda Lemma is the Fundamental Theorem of Computation. It is the mathematical expression of the following basic idea about computation: The validity of a computation is basically the same whether it is a self-standing program or whether it is one step in a larger program.

Here are the underlying ideas:

• If we stay within a category C, then all that matters are the morphisms, because the identity morphism can take the place of the associated object.
• And within a category C, we can think of the morphisms as possible actions that we can take.
• There are two kinds of morphisms: those that do nothing (identity morphisms) and those that do something (all the rest).
• A functor F:C->D takes us outside of our category. It is a program that takes actions in C and yields outputs in D.
• Here the D could be Set, but it's not yet clear to me how important that is, whether it could be List or something else.
• In order to run a morphism in C as a program we need two functors working in parallel. One functor F expresses the execution of the program and the other functor G expresses the output.
• A natural transformation is then the validation that the two functors F and G successfully work in parallel.
• The states of the program are the objects in D.
• Thus the action taken in C - which is a morphism that may be composed of a long path of actions - is implemented as a program in D which expreses such actions as changes in state and thus makes it possible to explicitly break down a program into steps and also separate its execution (the evolution of its internal states) and its possible outputs (its likewise evolving external states).

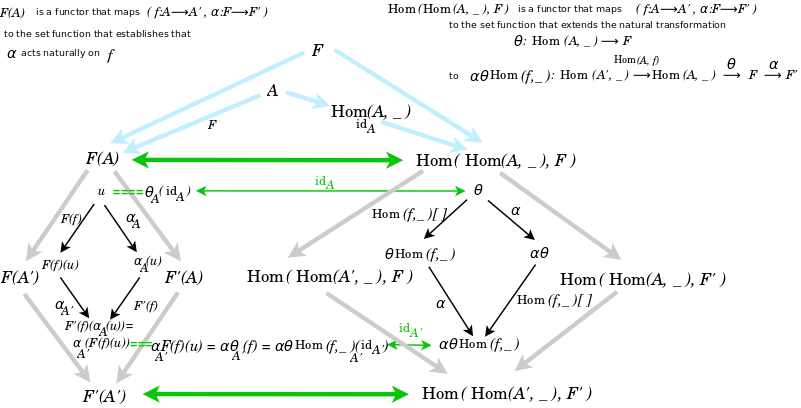
The Yoneda Lemma is a natural isomorphism between two functors, {$F(A)$} and {$Hom(Hom(A, \_ ), F)$}.

The functor {$( F(A) )$} takes, as it inputs, a natural transformation {$n:F\rightarrow G$} and a functor {$f:A\rightarrow B$}, and outputs a set function. That set function happens to be the one that validates that n is a natural transformation at f. Which is to say, it validates that a program makes sense on its own.

The functor {$( Hom(Hom(A, \_ ) , F) )$} likewise takes, as its inputs, a natural transformation n:F->G and a functor f:A->B, and outputs a set function. That set function maps natural transformations in {$( Hom(Hom(A, \_ ), F) )$} to natural transformations in {$( Hom(Hom(B, \_ ), G) )$}. Specifically, that set function takes an input, the natural transformation m, and outputs the natural transformation {$( nmHom(f, \_ ) )$} , which extends and leverages m so that it works in the new state. So here we are explicitly moving from a valid state (A,F) to valid state (B,G). Here we are saying that the computation is valid because it takes us from a state (A,F), where it works, to a state (B,G), where it works. Mathematically, the key idea is that the "do nothing" action id_A gets mapped to whatever "initial state" object in F(A) and all of the other "do something" actions in Hom(A,_ ) get mapped to "final state" objects in F(A). Then you get to a new valid state: f has taken you to B, and the old program F, which has been run, is now thought of as the new program G. And B has its own "do nothing" action id_B which becomes the "initial state" in G(B). In summary, the functor Hom(Hom(A, _ ), F) outputs a set function on natural transformations which is precisely the one that validates that we can keep going from initial state to initial state, step by step, as we run our program.

The upshot is that the functor F(A) doesn't identify any particular initial state but simply runs and validates all possible computations. And you don't have the concept of breaking down a program into steps or subroutines. Whereas the functor Hom(Hom(A, _ ), F) explicitly frames a single step as a subroutine in some conceivably larger program, and so moves us from an initial state to a final state, which becomes a new initial state. The Yoneda lemma is the machinery that shows that the validity is the same.

The idea leapt out when I drew a picture of the Hom(A,_ ) arrows in C, including id_A, and the related arrows in F(C), including the "initial state" that id_A gets mapped to.

From the step-by-step point of view, we can think of a natural transformation F->G as splitting a morphism=computation f in C into two perspectives: the execution F(f) and the outcomes G(f).

The Yoneda Embedding

The Yoneda embedding places in a wider context. Note that for automata this means that it increases the possible sophistication.

The Yoneda Lemma

Whether, What, How, Why

The distinction between the execution (How) and the output (What) seems very important.

With natural transformations, there is a distinction between the objects in C, used as indices of the components, and the diagram itself, which is entirely in D. I think C expresses How and D express What.

Example: Preorders

For pre-orders, the Yoneda Lemma says that {$x\leq y$} iff {$(\forall z)\, z\leq x \Rightarrow z\leq y.$} From left to right use transitivity of the preorder; from right to left, instantiate z to x, and use reflexivity.

A pre-order is a category where given objects X and Y, possibly equal, there is at most one morphism from X to Y.

Example: Graphs

category of graphs

• graphs as objects
• Graph homomorphisms as arrows (vertices to vertices and edges to edges)

Example: Dynamical systems

Example: Groups