Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

Split-biquaternions

Compare with split-complex numbers.

Will relate

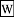• Split-biquaternions {$x+y\omega$} where {$\omega^2=1$} and {$x,y\in\mathbb{H}$}
• Clifford algebra {$x+y\epsilon_1$} as per the recursion: {$\mathbb{H}\otimes(\mathbb{R}\oplus\mathbb{R})$}
• Clifford algebra {$Cl_{0,3}(\mathbb{R})$} generated by {$e_1\rightarrow e_1\otimes 1, e_2\rightarrow e_2\otimes 1, e_3\rightarrow e_1e_2\otimes\epsilon_1$} where {$e_1^2=e_2^2=e_3^2=-1$} and {$\epsilon_1^2=1$}
• In other words, generated by {$i,j,k\omega$}.
• Direct sum {$(a,b)\in\mathbb{H}\oplus\mathbb{H}$}
• Matrix algebra

{$\begin{pmatrix} x & y\\ y & x \end{pmatrix}$}

{$\begin{pmatrix} x+y & 0\\ 0 & x-y \end{pmatrix}$}

{$\begin{pmatrix} \frac{a}{2} & \frac{a}{2} & 0 & 0 \\ \frac{a}{2} & \frac{a}{2} & 0 & 0 \\ 0 & 0 & \frac{b}{2} & \frac{-b}{2} \\ 0 & 0 & \frac{-b}{2} & \frac{b}{2} \end{pmatrix}$}

Matrix algebra

{$i(a_{11} + a_{12}i + a_{13}j + a_{14}k + a_{21}\omega + a_{22}i\omega + a_{23}j\omega + a_{24}k\omega) = -a_{12} + a_{11}i -a_{14}j + a_{13}k -a_{22}\omega + a_{21}i\omega - a_{24}j\omega + a_{23}k\omega$}

{$j(a_{11} + a_{12}i + a_{13}j + a_{14}k + a_{21}\omega + a_{22}i\omega + a_{23}j\omega + a_{24}k\omega) = -a_{13} + a_{14}i +a_{11}j-a_{12}k - a_{23}\omega + a_{24}i\omega + a_{21}j\omega - a_{22}k\omega$}

{$k\omega(a_{11} + a_{12}i + a_{13}j + a_{14}k + a_{21}\omega + a_{22}i\omega + a_{23}j\omega + a_{24}k\omega) = -a_{24}-a_{23}i+a_{22}j+a_{21}k -a_{14}\omega -a_{13}i\omega +a_{12}j\omega +a_{11}k\omega$}