Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

The factoring (number of simplexes n choose k - dependent simplex) x (number of flags on k - independent Euclidean) x (number of flags on n-k - independent Euclidean) = (number of flags on n)

The combinatorial interpretation of n-choose-k counts placements = "external arrangements" n! x...x (n-k+1)! and then divides by the redundancies = "internal arrangements" k! Thus it relates external and internal (within subsystem).

Conjugation gives the ways of relabeling, renaming. For example, (132)(12)(123) relables 1 as 2 and 2 as 3 in (12) to get (23).

I want to list and generate the basic combinatorial objects.

Stanley Enumerative Combinatorics

• Volume I
• Volume II: Table of Contents
• The Twelvefold Way
• Permutations
• Sieve methods - Inclusion Exclusion
• Partially ordered sets
• Rational generating functions
• Trees and the Composition of Generating Functions
• Algebraic, D-Finite, and Noncommutative Generating Functions
• Symmetric functions

The Twelvefold Way f:N->X two sets

• f is arbitrary (no restriction)
• f is injective (one-to-one)
• f is surjective (onto)

And regarding the elements of N and X as "distinguishable" or "indistinguishable".

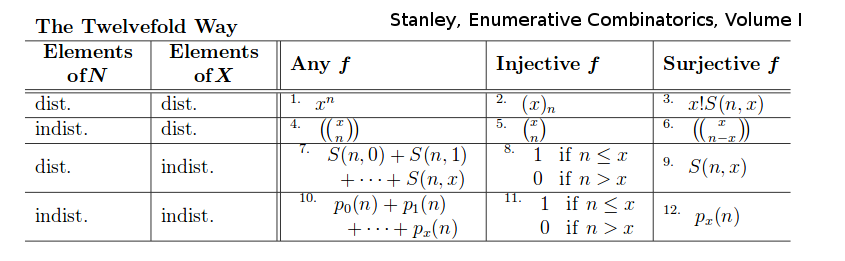
{$(x)_{n}=x(x-1)(x-2)...(x-n+1)$}

{$S(n,k)$} is the number of partitions of an n-set into k-blocks. It is called a Stirling number of the second kind.