Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

• Math Discovery Basic Three
• Math Discovery Algebra
• Math Discovery Analysis
• Math Discovery Learning Cycle
• Math Discovery Four Levels
• Math Discovery Six Pairs

Paul Zeitz, I share with you my thoughts on the varieties of "deep structure" in mathematical "frames of mind". Your book The Art and Craft of Problem Solving has been profoundly helpful. I also share with Joanne Simpson Groaney ("Mathematics in Daily Life"), Alan Schoenfeld ("Learning to Think Mathematically..."), John Mason ("Thinking Mathematically"), Manuel Santos, and also Maria Druojkova and the Math Future online group where I am active.

I have been looking for the "deep ideas" in mathematics. George Polya's book "Mathematical Discovery" documents four patterns (Two Loci, the Cartesian pattern, recursion, superposition) of the kind I'm looking for (and which bring to mind architect Christopher Alexander's pattern languages). Your book documents dozens more. I've found Joanne Groaney's book helpful and I think the other writings I mention will also be in this regard.

You note in your "planet problem", pg.63, that "on the surface" it is a nasty geometrical problem but "at its core" it is an elegant logical problem. This distinction brings to mind linguist Noah Chomsky's distinction between the surface structure and the deep structure of a sentence. In general, what might that deep structure look like? George Polya ends his discussion of the pattern of "superposition" or "linear combination" to say that it imposes a vector space. In an example he gives, the problem of "finding a polynomial curve that interpolates N points in the plane" is solved by "discovering a set of particular solutions which are a basis for a vector space of linear combinations of them". The surface problem has a deep solution, and the deep solution is a mathematical structure!

I list below 24 such deep structures which characterize the mathematical "frames of mind" by which we solve problems. I note in parentheses the related patterns, strategies, tactics, tools, ideas or problems. I have included every such that I have found in your book, as well as Polya's four patterns, "total order" and "weighted average" that I observed in Joanne Growney's book, and a few more that I know of. Please start with the illustrative example of constructing an equilateral triangle.

I Need to Sort These

Solutions to the problem of the brachistochrone

Alternatives to mathematical induction* Edward Cherlin: There are proofs that depend on the algebraic or topological nature of other mathematical structures, where you can't do induction because the underlying sets are not well-ordered. This is the essence of category theory and much of model theory.812

Epsilon induction* Wikipedia: In mathematics,-induction (epsilon-induction) is a variant of transfinite induction, which can be used in set theory to prove that all sets satisfy a given property P[x]. If the truth of the property for x follows from its truth for all elements of x, for every set x, then the property is true of all sets. ... This principle, sometimes called the axiom of induction (in set theory), is equivalent to the axiom of regularity.1578

Forcing (in set theory)* Wikipedia In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1962, to prove the independence of the continuum hypothesis and the axiom of choice from Zermelo-Fraenkel set theory. Forcing was considerably reworked and simplified in the 1960s, and has proven to be an extremely powerful technique both within set theory and in other areas of mathematical logic such as recursion theory. ... Perhaps more clearly, the method can be explained in terms of Boolean-valued models. In it, any statement is assigned a truth value from some infinite Boolean algebra, rather than just a true/false value. Then an ultrafilter is picked in this Boolean algebra, which assigns values true/false to statements of our theory. The point is that the resulting theory has a model which contains this ultrafilter, which can be understood as a model obtained by extending the old one with this ultrafilter. By picking a Boolean-valued model in appropriate way, we can get a model that has the desired property. In it, only statements which must be true (are "forced" to be true) will be true, in a sense (since it has this extension/minimality property).1159

Thought experiments in Computer Science* Wikipedia's list of thought experiments in Computer science: Halting problem (limits of computability), Turing machine (limits of computability), Two Generals' Problem, Dining Philosophers (computer science)859

Thought experiments in Mathematics* Thought experiments in Mathematics: Balls and vase problem (infinity and cardinality), Gabriel's Horn (infinity), Infinite monkey theorem (probability), Lottery paradox (probability), Sleeping beauty paradox (probability)857

Math Overflow: Bill Thurston. Thinking and explaining

• invariant
• "fall back on computation"
• attaching meaning to a term by evoking an image: Andy Gleason imagines the cyclic subgroups of a group as elements that fall into circular formations

Literature

• Paul Zeitz. The Art and Craft of Problem Solving at archive.org
• Zbigniew Michalewicz, David B. Fogel. How to Solve It: Modern Heuristics.

House of knowledge for math

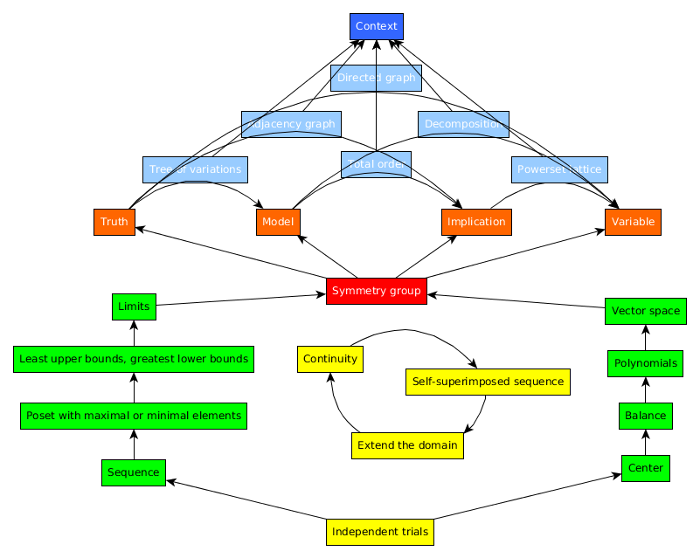
• Sequence (starting analysis) is an infinite list. A list (ending algebra).
• Limit (ending analysis) is similar to a center (starting algebra).

Ways of figuring things out in Math

• Delta-calculus is the analysis branch. Lambda-calculus is the algebra branch.
• The levels are given by the arithmetical hierarchy.
• Check this: Analysis: For every x (induction) there exists a y (max or min) such that for every z (greatest lower bound or least upper bound) there exists a w (limit)
• Algebra: There exists a C (center) such that for every B (balanced pair) there exists a S (set) such that for every L (list)
• Note that each quantifier takes us back and forth between two worlds (with adjunctions) as in statistics (the data world and the ideal world)
• Algebraic wayss: balanced pairs x:y, x=y
• Analytic ways: relationships x<y, x->y

Relate this to the arithmetical hierarchy