Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

On this page I am organizing a list of mathematical concepts that I wish to be able to account for. Sources of concepts include:

• List of mathematics topics
• List of mathematical examples

Basic ideas

• The most central concept in Math is duality, which is the basis for logic.
• The most fundamental symmetry is that of choice, as given by the ways we may interpret the binomial theorem, for it underlies the symmetry of algebraic expansions.

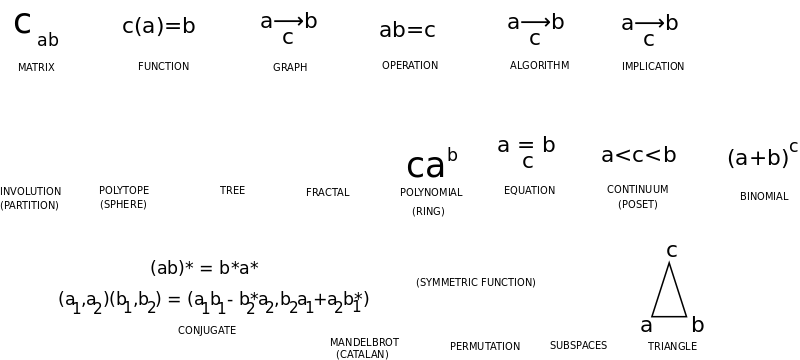
Matematikos savokų pagrindas yra dvejybinis-trejybinis - operacijos jungia du narius trečiu nariu. Matricų elementai sieja du narius ir išgauna trečią. Kategorijų teorija panašiai. O geometrija lygiaverčiai sieja tris narius trikampiais, įvairiai suprastais. Tad tai paaiškintų geometrijos svarbą.

Mathematical concepts

Variables

Duality

Objects? and their Symmetry

• combinatorial principles
• mathematical shapes
• polygons, polyhedra and polytopes
• regular polytopes - points on a circle or sphere, etc.
• partition topics
• factorial and binomial topics
• convexity topics

Binomial, Choice, Probability, Entropy

• Definite / deterministic (the) vs. Indefinite / Nondeterministic (a) - P vs. NP
• Axiom of Choice

Numbers Real, Complex, Quaternion

• Bott periodicity - Clifford Algebra shift clock - and Octonions
• Octonions
• Trialities and spinors
• Magic Square of Lie algebras
• matrices
• continuum
• order topics
• numeral system topics
• properties of sets of reals
• exceptional set concepts
• fractal topics

Infinity

Functions

• mathematical functions
• special functions and eponyms
• transforms
• Fourier-related transforms
• polynomial topics
• exponential topics
• logarithm topics

Equations

• equations
• inequalities
• mathematical identities
• formulae involving pi

Subspaces

• curves
• mathematical knots and links
• surfaces
• algebraic surfaces
• manifolds
• examples in general topology

Operations

• small groups
• finite simple groups
• simple Lie groups
• Table of Lie groups
• complex reflection groups
• permutation topics

Algorithms

• algorithms
• complexity classes

Proofs

• axioms
• conjectures
• lemmas
• mathematical proofs
• theorems

Particular concepts

• Catalan numbers are related to semantics and to the generating function of the mandelbtot set
• Universal cover. Wikipedia: The concept of a universal cover was first developed to define a natural domain for the analytic continuation of an analytic function. The idea of finding the maximal analytic continuation of a function in turn led to the development of the idea of Riemann surfaces. The power series defined below is generalized by the idea of a germ. The general theory of analytic continuation and its generalizations are known as sheaf theory.
• Covering spaces. Wikipedia: Covering spaces play an important role in homotopy theory, harmonic analysis, Riemannian geometry and differential topology. In Riemannian geometry for example, ramification is a generalization of the notion of covering maps. Covering spaces are also deeply intertwined with the study of homotopy groups and, in particular, the fundamental group. An important application comes from the result that, if X is a "sufficiently good" topological space, there is a bijection between the collection of all isomorphism classes of connected coverings of X and the conjugacy classes of subgroups of the fundamental group of X.
• Characteristic class? of different kinds are related to the classical linear groups.

Notes on concepts

• Function can be partial, whereas a permutation maps completely.
• Intrinsic ambiguity of propositions - every proposition is a general rule, which can be questioned or applied.

Consider how concepts arise. Rationality and irrationality relate linearity and integrality by way of a linear equation which may or may not have a solution, and solutions which may or may not have such an equation.

• Challenge problems:
  • Determine whether {$\pi + e$} is rational or irrational.
  • Determine whether {$\pi^e$} is rational or irrational.
• Basic concept: Orientation (of a simplex). Relates to determinant, homology, etc.
• Vector spaces are basic. What is basic about scalars? They make possible proportionality.
• Basic concepts are the ways of figuring things out.
• Basic concept - orientation = parity.
• Randomness. Random phenomena organize themselves around a critical boundary.
• Real line models separation (by cutting) and connectedness (by continuity). The separating cuts become locations (points) in their own right.
• The definition of a completely new and distinct entity comes from the oneness in the fluttering that dances in and out of all of the existing entitities. That fluttering cannot be any one of them.

Fourier analysis.

• The signal = the total stream = onesome.
• Proof and Progress. Thurston. Gives twenty ways of understanding derivatives. I can systematize them.
• Matematika išplaukia iš (poreikių tenkinimo) algoritmų taikymo, vedančio iš duotybių į bendrybes. O tos bendrybės įkūnija, išreiškia tam tikrus prieštaravimus, juos paverčia sąvokomis, kurias galima mąstyti toliau. Pavyzdžiui, apskritimas iškyla iš begalinės simetrijos visom kryptim, arba iš virve aprėpto ploto maksimalizavimo.

Richard Southwell describes how mathematical functions can be visualized by:

• (1) elements and arrows
• (2) Wiring diagrams
• (3) fibres
• (4) bouquets
• (5) graphs
• (6) ontology logs
• (7) categories

Associativity means that there is no need for an external observer to place parentheses. There is internal consistency. There is no need for an external sense of time. Time makes sense internally.