Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

Math concepts, Math Companion

---

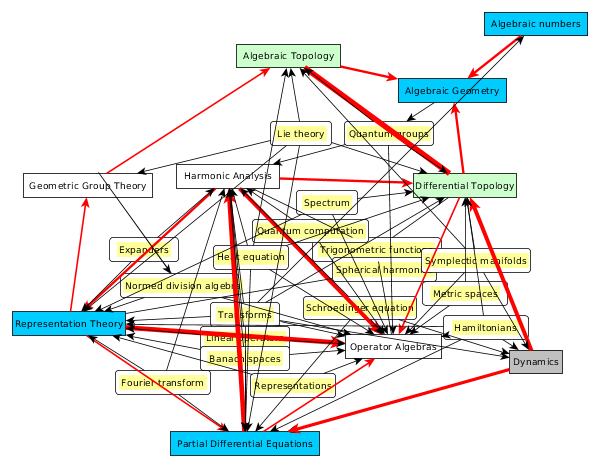
基本概念

• Orientation: Marked and unmarked opposites, outside and inside, antisymmetry, sign of permutation.
• Amounts: Summation. Identifying units (items, objects, areas, etc.) with numbers and adding them up.
• Smoothness: Change in one dimension is (extrinsically) comparable to (or even, intrinsically, of a much smaller order than) change in another dimension. Compare with difference between subconscious continuum and conscious discreteness.
• Generating functions relate: symmetry of analytic functions, algorithms, finite combinatorial symmetry. (Think of as a vector bundle - the infinite sequence ({$x_i$}) is the base space, and the coefficient is the fiber, and the fibers are related.)
• Linear operators - something you can have more of or less of (proportionately) - transformational action (like rotation or translation).

---

Math Companion Concepts

I am trying to organize the 99 concepts below. Next to each concept I have assigned the branches of math where they are important, with the 26 branches taken from the same Companion, and referenced by the numbers given in the book, as follows:

Axioms

22., 23. Zermelo-Fraenkel Axioms. Ways of constructing sets; of knowing if they are the same set; and of assuring that they don't have cycles.

22. Axiom of Choice. Given a set, you can select a representative element.

22. Axiom of Determinacy. The existence of a winning strategy for at least one of two players of an infinite game.

23., 22. Peano Axioms. Describes the natural numbers.

• Natural numbers

Numbers

11., 6., 26., 4. Pi

1., 22. Irrational and Transcendental Numbers

• Solutions and nonsolutions to linear equations, polynomials equations, with integer coefficients.

Functions and mappings

9. Determinants. Sum of oriented permutations = oriented volume of matrix.

18., 6., 17., 10a., 10b., B1. Knot Polynomials

18b., 18a. Generating Functions

2., 11. Exponential and Logarithmic Functions

X 11., 7., 15. Trigonometric Functions

XX 11., 9., 15., 7. Spherical Harmonics

12., 11., 21. Linear and Nonlinear Waves and Solitons

2. Gamma Function

2., 5. L-Functions

2., 5., 7. Riemann Zeta Function

22., 15., 25. Measures

1., 4., 6., 15. Quadratic Forms

12. Distributions

19 b., 22., 11., 26. Probability Distributions

7., 4., BX1. Differential Forms and Integration

X 9., 15., 23. Tensor Products

XXX 9., 15., 11., 12. Linear Operators and Their Properties

4. Modular Forms

6., 7., 10a., 1. Universal Covers. A space Y and a continuous surjection from Y to X.

6., 7. Vector Bundles. A space E and a continuous map p from E to X such that the inverse image {$p^{-1}(x)$} is an (n-dimensional) vector space.

25. Ising Model

Equations

12. Euler and Navier-Stokes Equations

XX 12., 11., 15., 7., 6. Heat Equation

XX 12., 14., 15., 24., 25., 11. Schroedinger Equation

12., 18., 21., 11., 19b. Special Functions

4. Elliptic Curves

Identifications

XX 11., 9., 12., 26. Fourier Transform

• Use complex roots {$e^{ir\theta}$} as set of frequencies to identify sequence and function.

11. Fast Fourier Transform

XXX 11., 15., 12., 19b., 18., 7., 2., 14., 9. Transforms

• Identifies sequence (and its self-symmetry) and function (and its self-symmetry).

Objects - Structures

22. Countable and Uncountable Sets

14. Mandelbrot

22. Ordinals

22. Cardinals

23., 6. Categories

19a. Graphs

X 18., 20., 11., 9. Expanders

10a. Buildings

10a., 9. Leech Lattice

4., 5. Varieties

20., 9., 18. Matroids

3., 10b. Modular Arithmetic

10a., 12., 6. Fuchsian Groups

X 5., 4., 15., 7., 6., 11., 23. Quantum Groups

• Algebras of polynomials up to equivalence on a variety - where the points are group elements.
• Map from X to Y gives rise to adjoint map from C[Y] to C[X].
• Algebras has coproduct. Group structure yields Hopf algebra or quantum group (which has additional structure analogous to that of a Lie group).
• Makes sense over any field.
• There exist noncommutative Hopf algebras based on deformations q, thus grounding noncommutative geometry.
• Hopf algebras are the next simplest categories after abelian groups that admit a Fourier transform.
• Axioms of Hopf algebra are symmetric under arrow reversal.
• Bicrossproduct quantum groups are simultaneously coordinate algebras and symmetry algebras.

1. Galois Groups

6., 4. Braid Groups

1. Ideal Class Group

10b., 9., 17. Monster Group

10b., 9., 19b. Permutation Groups

1., 4., 9. Rings, Ideals, and Modules

4., 1., 5. Schemes

1. Number Fields

X 9., 15. Representations

X 9., 15., 10a. Quaternions, Octonions and Normed Division Algebras

23., 22. Models of Set Theory

Spaces

4., 6. Projective Space

7., 6., 4., 8. Manifolds

7., 4., 16. Calabi-Yau Manifolds

X 7., 22., 18., 20., 13., 15. Metric Spaces

7., 6., 11., 10a. Riemann Surfaces

X 7., 6., 15., 14., 24. Symplectic Manifolds

4., 7., 16. Orbifolds

15. C*-Algebras

15. Function Spaces

15., 11. Hilbert Spaces

6., 7., 4. Topological Spaces

8., 6., 7., 4., 1., 11. Moduli Spaces

XX 15., 12., 11., 9. Normed Spaces and Banach Spaces

15. Von Neumann Algebras

Properties and invariants

7., 14. Dimension

13., 7. Curvature

7. Compactness and Compactification

6., 7., 4. Genus

XX 14., 12., 15., 9., 17., 16., 7. Hamiltonians

X 15., 9., 7. Spectrum

9., 10 b. Jordan Normal Form

14., 12. Dynamical Systems and Chaos

25. Phase Transitions

Algorithms

2. Euclidean Algorithm and Continued Fractions

14., 7., 12., 11., 24. Variational Methods

X 20., 11., 15., 19b., 26. Quantum Computation

20., 9., 14., 10a., 18. Simplex Algorithm

21., 11. Wavelets

20. Computational Complexity Classes

7., 6., 12. Ricci Flow. Replaces a manifold with a smoother manifold.

14., 12., 7. Optimization and Lagrange Multipliers

High level concepts

10a., 4., 6., 16. Duality

1., 2., 4. Local and Global in Number Theory

Theories

X 9., 6., 10a., 10b., 12., 17., 7. Lie Theory

6. Homology and Cohomology

6., 15. K-Theory

---