- MathNotebook
- MathConcepts
- StudyMath
- Geometry
- Logic
- Bott periodicity
- CategoryTheory
- FieldWithOneElement
- MathDiscovery
- Math Connections
Epistemology
- m a t h 4 w i s d o m - g m a i l
- +370 607 27 665
- My work is in the Public Domain for all to share freely.
- 读物 书 影片 维基百科
Introduction E9F5FC
Questions FFFFC0
Software
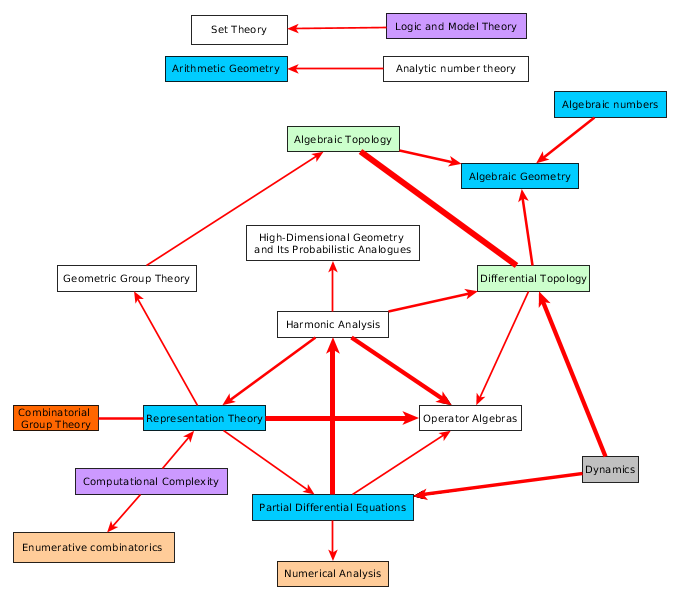
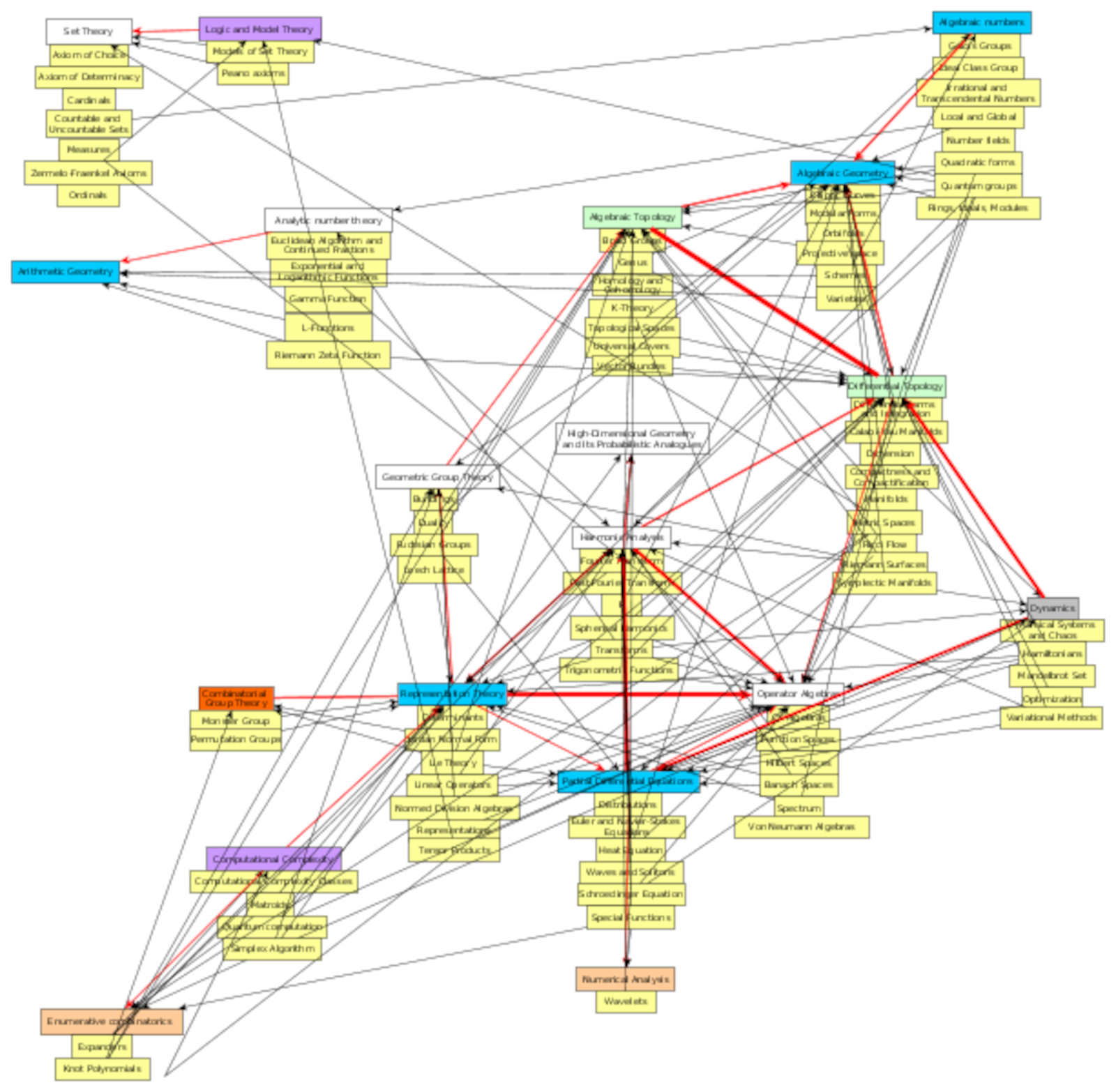
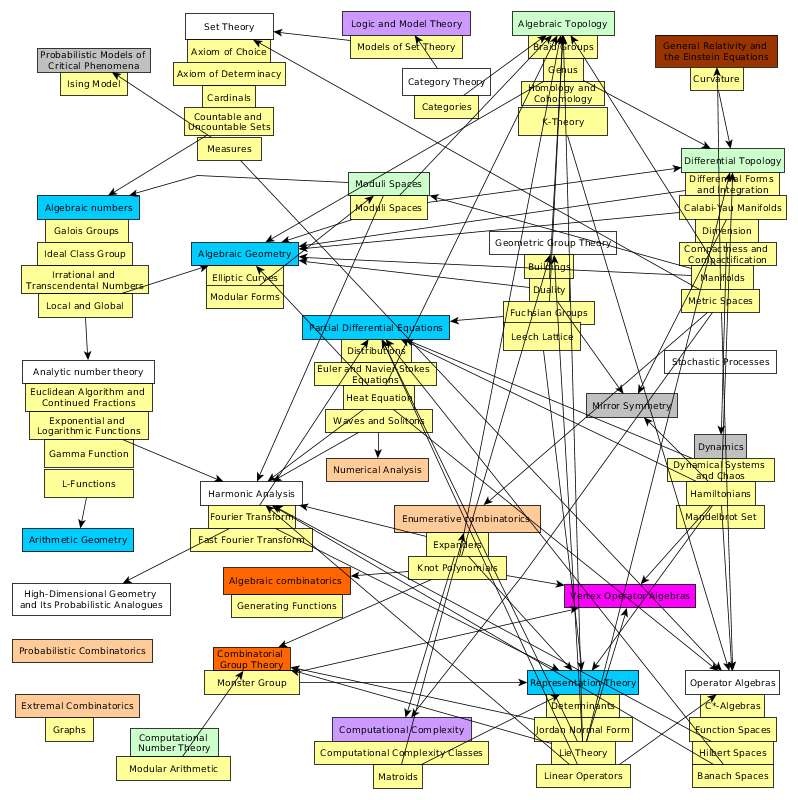
Map of math, Math constants, Math functions, Theorems, Math Companion concepts
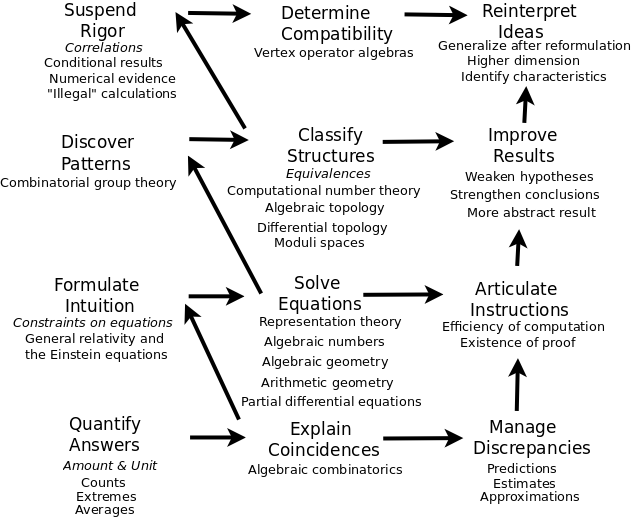
I'm organizing the concepts in The Princeton Companion to Mathematics.
- What is the place for geometric constructions?
Mathematical answers
Quantify answers
- N Exact counting (Listing) S= 18a. Enumerative combinatorics (polynomial time algorithms for computation)
- 18., 20., 11., 9. Expanders
- 18., 6., 17., 10a., 10b., B1. Knot Polynomials
- N An Extremal problems S= 19a. Extremal Combinatorics
- 19a. Graphs
- N Averages S= 19b. Probabilistic combinatorics
- 19 b., 22., 11., 26. Probability Distributions
Explain coincidences
- S= 18b. Algebraic combinatorics (interpreting formulas)
- 18b., 18a. Generating Functions
Manage discrepancies
- N An Estimates S= 2. Analytic number theory
- 2. Euclidean Algorithm and Continued Fractions
- 2., 11. Exponential and Logarithmic Functions
- 2. Gamma Function
- 2., 5. L-Functions
- 2., 5., 7. Riemann Zeta Function
- Algo An Approximations S= 21. Numerical analysis (algorithms for approximating the continuum)
- 21., 11. Wavelets
- Al An Predictions S= 24. Stochastic processes (model the evolution of random phenomena)
Formulate intuition as constraints on equations
- G An E= 13. General relativity and the Einstein equations (expressing, interpreting and validating a theory of physics)
- 13., 7. Curvature
Solve equations. Any solutions? Unique solution? Constraints on solutions?
- Al G Linear equations. S= 9. Representation Theory
- 9. Determinants
- 9., 10 b. Jordan Normal Form
- 9., 6., 10a., 10b., 12., 17., 7. Lie Theory
- 9., 15., 11., 12. Linear Operators and Their Properties
- 9., 15. Representations
- 9., 15., 10a. Quaternions, Octonions and Normed Division Algebras
- 9., 15., 23. Tensor Products
- N Al Polynomial equations. S= 1. Algebraic numbers
- 1. Galois Groups
- 1. Ideal Class Group
- 1., 22. Irrational and Transcendental Numbers
- 1., 2., 4. Local and Global in Number Theory
- 1., 4., 6., 15. Quadratic Forms
- 1. Number Fields
- 1., 4., 9. Rings, Ideals, and Modules
- G Al Polynomial equations in several variables. S= 4. Algebraic geometry
- 4. Elliptic Curves
- 4. Modular Forms
- 4., 6. Projective Space
- 4., 7., 16. Orbifolds
- 4., 1., 5. Schemes
- 4., 5. Varieties
- N G Diophantine equations. S= 5. Arithmetic geometry
- 5., 4., 15., 7., 6., 11., 23. Quantum Groups
- An Al Differential equations. S= 12. Partial differential equations
- 12. Distributions
- 12. Euler and Navier-Stokes Equations
- 12., 11., 15., 7., 6. Heat Equation
- 12., 11., 21. Linear and Nonlinear Waves and Solitons
- 12., 14., 15., 24., 25., 11. Schroedinger Equation
- 12., 18., 21., 11., 19b. Special Functions
Articulate instructions. Find explicit proofs and algorithms
- Algo N S= 20. Computational complexity (what can be computed efficiently or not)
- 20. Computational Complexity Classes
- 20., 9., 18. Matroids
- 20., 11., 15., 19b., 26. Quantum Computation
- 20., 9., 14., 10a., 18. Simplex Algorithm
- F Al S= 23. Logic and model theory (formal languages about mathematical structures, whether a proof exists or not)
- 23., 6. Categories
- 23., 22. Models of Set Theory
- 23., 22. Peano Axioms
Discover patterns
- Al N S= Groups (symmetries), 10b. Combinatorial group theory (groups in terms of their generators and relations)
- 10b., 9., 17. Monster Group
- 10b., 9., 19b. Permutation Groups
Classify structures.
- N Algo Building blocks and combinations. E= 3. Computational number theory (identifying primes as components or in totality)
- 3., 10b. Modular Arithmetic
- Families and exceptions. E= Algebraic topology
- G An Transformation demonstrates equivalence. E= 7. Differential topology (classifying smooth manifolds - list all smooth structures on any topological manifold and be able to identify them - a certain set of discrete subgroups of the isometry group of any one of the eight model spaces determines a compact manifold with the corresponding geometric structure)
- 7., 6., 4., 8. Manifolds
- 7., 4., BX1. Differential Forms and Integration
- 7., 4., 16. Calabi-Yau Manifolds
- 7., 14. Dimension
- 7. Compactness and Compactification
- 7., 22., 18., 20., 13., 15. Metric Spaces
- 7., 6., 12. Ricci Flow
- 7., 6., 11., 10a. Riemann Surfaces
- 7., 6., 15., 14., 24. Symplectic Manifolds
- G Al Invariant demonstrates nonequivalence. E= 6. Algebraic topology
- 6., 4. Braid Groups
- 6., 7., 4. Genus
- 6. Homology and Cohomology
- 6., 15. K-Theory
- 6., 7., 4. Topological Spaces
- 6., 7., 10a., 1. Universal Covers
- 6., 7. Vector Bundles
- G An Map to a structure E= 8. Moduli spaces (give a geometric structure to the totality of the objects we are trying to classify)
- 8., 6., 7., 4., 1., 11. Moduli Spaces
Improve results
- An N Weaken hypotheses. E= 15. Operator algebras (expanding from finite-dimensional equations to integral equations)
- 15. C*-Algebras
- 15. Function Spaces
- 15., 11. Hilbert Spaces
- 15., 12., 11., 9. Normed Spaces and Banach Spaces
- 15., 9., 7. Spectrum
- 15. Von Neumann Algebras
- An G Strengthen conclusions. E= 11. Harmonic analysis (determining the properties of functions that are not explicitly describable, for example, the effect of operators on the boundedness of functions)
- 11., 9., 12., 26. Fourier Transform
- 11. Fast Fourier Transform
- 11., 6., 26., 4. Pi
- 11., 9., 15., 7. Spherical Harmonics
- 11., 15., 12., 19b., 18., 7., 2., 14., 9. Transforms
- 11., 7., 15. Trigonometric Functions
- Prove a more abstract result. E= Category theory
Suspend rigor. Work with arguments that are not fully rigorous.
- An Algo E=Conditional results = 14. Dynamics (how systems evolve in time)
- 14., 12. Dynamical Systems and Chaos
- 14., 12., 15., 9., 17., 16., 7. Hamiltonians
- 14. Mandelbrot
- 14., 12., 7. Optimization and Lagrange Multipliers
- 14., 7., 12., 11., 24. Variational Methods
- Al An E=Numerical evidence. = 25. Probabilistic models of critical phenomena (modeling thresholds for divergent outcomes)
- 25. Ising Model
- 25. Phase Transitions
- An G E="Illegal" calculations. = 16. Mirror symmetry (reformulating a physical theory's information in a mirror theory)
Determine compatibility. Whether different mathematical properties are compatible.
- An Al E= 17. Vertex operator algebras (formulating perspective: relating quantum data and space-time manifold)
Reintrepret ideas.
- Al G Identify characteristic properties. E= 10a. Geometric group theory (groups in terms of their actions expressed geometrically)
- 10a. Buildings
- 10a., 4., 6., 16. Duality
- 10a., 12., 6. Fuchsian Groups
- 10a., 9. Leech Lattice
- N F Generalize after reformulation P= 22. Set theory (distinguishing between cardinals-sets and ordinals-lists and relating the two)
- 22. Axiom of Choice
- 22. Axiom of Determinacy
- 22. Cardinals
- 22. Countable and Uncountable Sets
- 22., 15., 25. Measures
- 22. Ordinals
- 22., 23. Zermelo-Fraenkel Axioms
- G N Higher dimensions and several variables. E= 26. High-dimensional geometry and its probabilistic analogues (most efficient boundary for volume, the sphere, models random distributions)
N Numbers, G Geometry, Al Algebra, Algo Algorithms, An Analysis, P Proof, F Foundations
- B1. Chemistry
- B2. Biology
- B3. Wavelets and Applications
- B4. Traffic in Networks
- B5. Algorithm Design
- B6. Reliable Transmission of Information
- B7. Cryptography
- B8. Economic Reasoning
- B9. Money
- B10. Statistics
- B10. Bayesian Analysis
- B10., B6., Designs
- B11. Medical Statistics
- B12. Philosophical Analysis
- B13. Music
- B14. Art
- BX1. Physics
Consider underlying assumptions. Counting, averaging, extremes - all suppose "many".
Are the math answers expressing the 12 topologies? Should there be two more kinds?
Ideas
Bifurcation of topics
- Continuity vs. Topology (properties that are not affected by continuous transformations)
- Factorization vs. Primes
Consciousness - matching the unconscious and the conscious - is like solving an equation.