Math 4 Wisdom. "Mathematics for Wisdom" by Andrius Kulikauskas.

Yoneda Lemma, Learning Yoneda Lemma, Yoneda Lemma Top Down

Mastering the Yoneda Lemma

I have made three or four attempts to learn the basics of category theory. At this point, I know enough to have some opinions, raise some questions, and study on my own. But it is very helpful to be able to exchange thoughts with others or at least think out loud. One of my particular goals is to master the Yoneda lemma. I think I am getting pretty close. So I feel comfortable enough to start this thread. I welcome any thoughts remotely relevant to understanding the Yoneda lemma and category theory in general.

I will start with my motivation. I am interested to know everything and apply that knowledge usefully. The way I work on this is to study the limits on my imagination. I have been documenting a variety of conceptual frameworks which constitute these limits. In the last several years I have been exploring links with mathematics. Here are the texts of my talks on these various subjects.

In particular, the Yoneda lemma reminds me of a conceptual structure which I call the foursome, the division of everything into four perspectives, four levels of knowledge: Whether, What, How, Why. These four levels come up often in philosophy and other settings. If I have a bottle, then I can consider its sensory image (What), or I can think of it as a blueprint, how we create it and use it (How). These are human, every day levels of knowledge. But I can also imagine that I know absolutely everything about the bottle, how it relates to absolutely everything, my hand, the room, plastic, China, atoms, the origin of the universe, and so on. All of that knowledge would be in my mind, and so the bottle need not actually exist, as it is all in my mind. This is the level (Why). Or I could hide the bottle in a cabinet, where nobody sees it. Is it there? This is the level (Whether).

The Yoneda lemma seems to relate these very concepts. It lets us think about an object in terms of all of its relations (Why). We also think of an object in terms of its identity morphism, that it is itself (Whether). And every morphism sends us from a richer category to a poorer category, like going from How to What. So it seems worthwhile to me to truly master the Yoneda lemma so that I could explain to myself and others with confidence what it says about these concepts.

I have made a list of how I study the Yoneda lemma. Perhaps you will suggest more ways?

As I wrote, I am interested to understand it intuitively, and also, cognitively. Where in our lives, and in our thinking, do we use the Yoneda lemma without even knowing it? I expect the essence of the Yoneda lemma to be something basic to our every day thinking.

I am interested in the purpose of the Yoneda lemma. I am grateful to Tai-Danae Bradley for her three part series where she writes a lot about that. In my understanding, it relates internal structure and external relationships, and that is perhaps the major theme of category theory. Also, it leverages the category Set, in particular. And it allows for the Yoneda embedding of any category into a category of (contravariant set valued) functors defined on that (opposite) category.

It's crucial to work through the mechanics of the statement and proof of the Yoneda lemma, as at Wikipedia. On the one hand, it's just a single commutative diagram. On the other hand, there are lots of layers of abstraction. And a key hurdle for me, again and again, is to learn to think that category theory is about functors. I have to unthink my inclination to think that they are maps between objects, and rather insist on thinking that they are maps between morphisms. In fact, it's really about maps between chains of morphisms, because it's crucial that composition and associativity be ever respected. There is much left unspoken in a commutative diagram. I have talked a few times with Eduardo Ochs, and read through his draft A skeleton for the proof of the Yoneda Lemma and his slides A diagram for the Yoneda lemma. He champions a sympathetic movement, "Logic for Children", which variously seeks to make these topics comprehensible. One thing he does is to explicitly diagram what is left unsaid, the internal logic that is supposed by mathematicians when they see a commutative diagram. I haven't worked with his texts enough to gain much from them. Instead, I have done something similar with the following diagram:

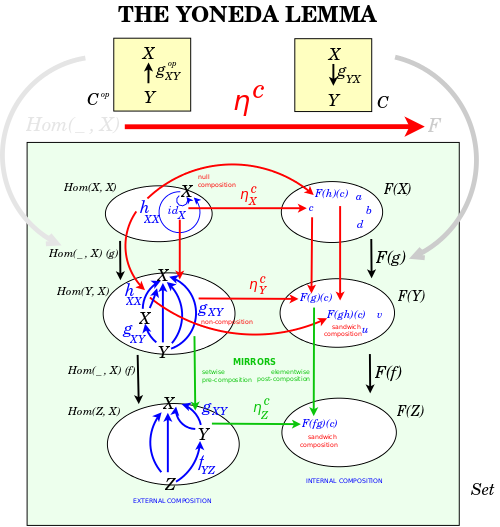
What I figured out from making that diagram are a few points that seem important. Every object has at least one morphism to itself (the identity morphism). Every set function has at least one element in its range. And, finally, composition of functions and of arrows seems to work in opposite directions. But this is still not enough to understand!

So currently I am working on a top down understanding, as opposed to the bottom up understanding I just described. A top down understanding says, ignoring all the details, What is the Yoneda lemma about? And then it says, well, it's about a natural isomorphism. This immediately forces me to realize that it's not just a bijection. I then slowly add more detail. I am working on that here and will write about that in subsequent posts. But I will mention that Eduardo Ochs really got me hopeful when he wrote for me: {$ \mathrm{Hom}(B,C) \leftrightarrow \mathrm{Nat}((C\rightarrow \;\;),(B\rightarrow \;\; )) $} I could start to imagine: {$ (\mathrm{How}\rightarrow\mathrm{What}) \rightarrow ((\mathrm{What}\rightarrow \;\; ) \rightarrow (\mathrm{How}\rightarrow \;\; )) $}

After working on the top down approach, I will want to try again to understand what the Yoneda lemma means in special cases, such as with Cayley's theorem for groups. I liked very much Richard Southwell's two-and-a-half hour video on the Yoneda lemma. He specifically talks, in the beginning, about a category of graphs, and in the end, about the category of dynamical systems.

As I learn more, I will want to understand the role of the Yoneda lemma and the Yoneda embedding in various areas of math. For example, the Yoneda lemma is the basis for the concepts of internal hom and closed category, which are necessary for working with Cartesian closed categories in logic, programming and computation, and for a topos. Symmetric monoidal closed categories are the subject of the Isbell duality which relates geometry and algebra.

Aside from all of these ways of approaching the Yoneda lemma, I have also made a list of obstacles in my attempts to learn category theory. Surveying such obstacles helps me understand the subject - that is my own version of the Yoneda lemma - rather than study the subject, I will study the obstacles!

Now I will share my work on the top down approach.

The Yoneda lemma is about an isomorphism. An isomorphism is a pair of natural transformations. And we could launch into the nuts and bolts of those natural transformations. But a top down approach suggests instead that those nuts and bolts can wait.

Instead, I realize that a natural transformation is simply a morphism in a functor category. So an isomorphism is a pair of morphisms, back and forth, between two objects in the functor category, which is to say, between two functors.

In the Yoneda lemma, that functor category is {$ \mathbf{Set}^{\mathbf{Set}^C \times C} $} Its objects are the functors that map morphisms in {$ \mathbf{Set}^C \times C $} to morphisms in {$ \mathbf{Set} $}.

I am giving some thought to this functor category and the two morphisms that the Yoneda lemma sets up within it.

In the Wikipedia article, the Yoneda lemma is stated like this: {$ \textrm{Nat}(h^A,F)\cong F(A) $}. As I delved into this, top down, this expression seemed to obscure the meaning. Hom-sets are sets of morphisms, and natural transformations are simply the morphisms in a functor category. So I rewrote it like this:

{$ \textrm{Hom}(\textrm{Hom}(A,–),F)\cong F(A) $}

Then I noticed a prevalent, inherent ambiguity between functors and their domains. (By analogy, the expression f(x) can be thought of as a function and the value of the output.) So I thought I would use the set notation to emphasize that the Hom-set can be thought of as a set and as a functor. So I rewrote it like this:

{$ \{ \{ A\rightarrow \_ \}\rightarrow F(\_) \}\cong F(A) $}

Then I realized that {$ F $} is also a functor and I wanted to bring that out. So, finally, I rewrote it like this:

{$ \{ \{ A \rightarrow \_ \} \rightarrow ( \_ \overset{F}{\rightarrow} \underset{F( \_ )}{ \{ \;\;\;\;\; \} }) \}\cong A \overset{F}{\rightarrow}\underset{F(A)}{ \{ \;\;\;\;\; \} } $}

Now, if you have mastered all of the layers in the expression {$ \textrm{Nat}(h^A,F)\cong F(A) $}, then that may be a very good way to write it out, because each layer gets differentiated. But I prefer these other expressions because I want to expose the layers involved and I want to appreciate the internal symmetry in the statement and figure out the essence of its meaning. In particular, I will work with the final expression because it manifests that the functor {$ F $}, the Hom-set, and the natural transformations are all just morphisms, in one category or another.

So now I have gotten to the specific reason why I decided to write this post. I'm trying to make sense of this expression, from a top down point of view:

{$ \{ \{ A \rightarrow \_ \} \rightarrow ( \_ \overset{F}{\rightarrow} \underset{F( \_ )}{ \{ \;\;\;\;\; \} }) \}\cong A \overset{F}{\rightarrow}\underset{F(A)}{ \{ \;\;\;\;\; \} } $}

Or, more tersely:

{$ L \cong R $}

It's expressing a natural isomorphism in the functor category {$ \mathbf{Set}^{\mathbf{Set}^C \times C} $} . Which is to say, it is expressing two morphisms, one from left-to-right, {$ L \rightarrow R $}, and the other from right-to-left, {$ L \leftarrow R $}. And these morphisms relate two objects, the left hand side {$ L $}, and the right hand side {$ R $}. I am trying to understand what each side means, starting with the right hand side.

Each side is an object in that functor category, which is to say, it is a functor. And these functors take as input a pair {$ (\alpha, f) $} where {$ \alpha $} is a natural transformation (a morphism) in {$ \mathbf{Set}^C $}, and {$ f $} is a morphism in {$ C $}. And they output a morphism in {$ \mathbf{Set} $}, which is to say, a set function. So what does that mean for {$ A \overset{F}{\rightarrow}\underset{F(A)}{ \{ \;\;\;\;\; \} } $} ?

Well, let's be more explicit and say {$ (\alpha, f): (G,X) \rightarrow (H,Y) $}. What is the output for the right-hand-side {$ R $} ? It should be a set function.

The fact that {$ (\alpha, f) $} is a morphism in {$ {\mathbf{Set}^C \times C} $} means that the following commutative diagram holds:

{$ \matrix{ G(X) & \overset{\alpha_X}{\longrightarrow} & H(X) \cr \downarrow{\scriptsize G(f)} & & \downarrow {\scriptsize H(f)} \cr G(Y) & \overset{\alpha_Y}{\longrightarrow} & H(Y) \cr } $}

Note that {$ G(X) $}, {$ G(Y) $}, {$ H(X) $}, {$ H(Y) $} are all sets. The commutative diagram describes for us the set function that we seek as the output. The set function sends {$ z \in G(X) $} to {$ \alpha_Y(G(f)(z)) = H(f)(\alpha_X(z)) \in H(Y) $}.

In summary, we see that {$ R $} is a functor defined as sending any morphism {$ (\alpha, f) $} to the set function {$ \alpha_Y(G(f)(z)) = H(f)(\alpha_X(z)) $}. Importantly, the morphism {$ \alpha $} in {$ \mathbf{Set}^C $} and the morphism {$ f $} in {$ C $} are completely arbitrary. Notice also, that this all works the same if we replace {$ \mathbf{Set} $} with a generic category {$ D $}.

The upshot is that the functor {$ R \equiv A \overset{F}{\rightarrow}\underset{F(A)}{ \{ \;\;\;\;\; \} } $} takes as input the pair of morphisms {$ (\alpha, f) $} and outputs the function defined by the commutative diagram which relates {$ \alpha $} and {$ f $}. In category theory, this expresses the most basic thing we do, as far as I know.

So this is what lurks in the expression {$ F(A) $}. And it expands greatly on the notion of "plugging in" suggested by {$ A \overset{F}{\rightarrow}\underset{F(A)}{ \{ \;\;\;\;\; \} } $}. This is because we have to think in terms of morphisms rather than objects. Then we see that {$ R $} is the incredible functor which establishes, I think universally, that all of the commutative diagrams hold for all of the natural transformations. And it does so by outputting the function which the commutative diagram computes. Thus the functor {$ R $} is establishing substitution as natural. The supposition for this is simply that the categories {$ C $} and {$ D^C $} are well founded.

Now I will consider the left-hand side {$ L $}.

{$ \{ \{ A \rightarrow \_ \} \rightarrow ( \_ \overset{F}{\rightarrow} \underset{F( \_ )}{ \{ \;\;\;\;\; \} }) \} $}

It is an object in the functor category {$ \mathbf{Set}^{\mathbf{Set}^C \times C} $} Thus, as a functor, it takes a morphism {$ ( \alpha, f) $} in {$ \mathbf{Set}^C \times C $} to a set function {$ \theta $} in {$ \mathbf{Set} $}. Here {$ \alpha : G \rightarrow H $} is a morphism (a natural transformation) in {$ \mathbf{Set}^C $} and {$ f: X \rightarrow Y $} is a morphism in {$ C $}.

What is the set function {$ \theta $} that it is producing? It is related to the set of natural transformations from functor {$ \{ A \rightarrow \_ \} $} to functor {$ \_ \overset{F}{\rightarrow} \underset{F( \_ )}{ \{ \;\;\;\;\; \} } $}. Note that both of these functors are objects in {$ \mathbf{Set}^C $}, which means that they both are functors from {$ C $} to {$ \mathbf{Set} $}.

To make sense of {$ L $}, which is a functor, it is important to understand what it does to morphisms, rather than isolated objects. Thus, instead of the object {$ A $} in {$ C $}, I am thinking of a morphism {$ f:X\rightarrow Y $}, and instead of the object {$ F $} in the functor category {$ \mathbf{Set}^C $} , I am thinking of a morphism {$ \alpha : G \rightarrow H $}. The input {$ ( \alpha, f) $} should yield a set function {$ \theta $} that takes us from one set to another. What are those sets and what is that function?

Here my impulse is to set up a commutative diagram that relates {$ \alpha $} and {$ f $}.

I start with {$ f $}, which is a morphism in {$ C $}. Thus it is an input for the functor {$ \{ A \rightarrow \_ \} $} and also for the functor {$ \_ \overset{F}{\rightarrow} \underset{F( \_ )}{ \{ \;\;\;\;\; \} } $}.

The functor {$ \{ A \rightarrow \_ \} $} maps the morphism {$ f:X\rightarrow Y $} to the set function {$ \{ A \overset{ \_ }{\rightarrow} X \overset{f}{\rightarrow} Y \} $} which maps the set {$ \{ A \rightarrow X \} $} to the set {$ \{ A \rightarrow Y \} $} by taking an element of the form {$ A \overset{\epsilon}{\rightarrow} X $} and mapping it to the element {$ A \overset {\epsilon}{\rightarrow} X \overset {f}{\rightarrow} Y $}. Note that the {$ \{ A \rightarrow X \} $} is the set of morphisms from {$ A $} to {$ X $} and may be possibly empty or have one or more different elements, which are the possible inputs for the set function {$ \{ A \overset{ \_ }{\rightarrow} X \overset{f}{\rightarrow} Y \} $}.

The functor {$ \_ \overset{F}{\rightarrow} \underset{F( \_ )}{ \{ \;\;\;\;\; \} } $} maps the morphism {$ f:X\rightarrow Y $} to the set function {$ \underset{F(X)}{ \{ \;\;\;\;\; \} } \overset{F(f)}{\rightarrow} \underset{F(Y)}{ \{ \;\;\;\;\; \} } $}, which is to say, the set function {$ F(X) \overset{F(f)}{\rightarrow} F(Y) $}.

I now consider the morphism (the natural transformation) {$ \alpha : G \rightarrow H $} in {$ \mathbf{Set}^C $}. Note that the functors {$ F $}, {$ G $}, {$ H $} and {$ \{ A \rightarrow \_ \} $} are all objects in {$ \mathbf{Set}^C $}. The first three functors are quite generic whereas the functor {$ \{ A \rightarrow \_ \} $} is defined in terms of an object {$ A $} in {$ C $}.

One point to make here is that a functor is much more than just a morphism. A morphism goes from one particular object to another particular object. Likewise, being a morphism, a functor goes from one particular category {$ C_1 $} to another particular category {$ C_2 $} . But in doing so, it must map absolutely all of the morphisms (and their objects) in {$ C_1 $}. Whereas a natural transformation is simply a morphism and not a functor. A natural transformation {$ \alpha $} goes from some particular functor {$ G $} to some other particular functor {$ H $}. However, {$ L $} is a functor, and so its inputs are general, and they include absolutely any pairs consisting of {$ \alpha $} in {$ \mathbf{Set}^C $} and {$ f $} in {$ C $}.

Thus I want to set up a commutative diagram that will relate absolutely any {$ \alpha $} in {$ \mathbf{Set}^C $} and {$ f $} in {$ C $}. Well, I can't relate such a generic {$ \alpha:G \rightarrow H $} to a not so generic functor {$ \{ A \rightarrow \_ \} $}. However, I can relate a generic {$ \alpha $} to the expression of a likewise generic functor {$ \_ \overset{F}{\rightarrow} \underset{F( \_ )}{ \{ \;\;\;\;\; \} } $}. Namely, I can write:

{$ ( \_ \overset{G}{\rightarrow} \underset{G( \_ )}{ \{ \;\;\;\;\; \} }) \overset{\alpha}{\underset {\alpha_{\_}}{\rightarrow}} (\_ \overset{H}{\rightarrow} \underset{H( \_ )}{ \{ \;\;\;\;\; \} } ) $}

Or simply: {$ G( \_ ) \overset{\alpha}{\underset {\alpha_{\_}}{\rightarrow}} H( \_ ) $} Here I write {$ \overset{\alpha}{\underset {\alpha_{\_}}{\rightarrow}} $} to note that there are two levels at work here. The natural transformation {$ \alpha $} maps the functor {$ G $} to the functor {$ H $}. And the component {$ \alpha_{\_} $} is a set function that maps the set {$ G( \_ ) $} to the set {$ H( \_ ) $} and satisfies the conditions on the natural transformation's commutativity diagram. So here I am noticing a map from our natural transformation {$ \alpha $} to a set function {$ \alpha_{\_} $}.

Note an important fact about natural transformations: this component {$ \alpha_{\_} $} is itself entirely in {$ \mathbf{Set} $}, but it is indexed by an object in {$ C $}. Indices are signs that leverage knowledge How. So now I am expecting that these components are important for distinguishing What and How.

Having learned about the inputs {$ f $} and {$ \alpha $}, and the functors {$ \{ A \rightarrow \_ \} $} and {$ \_ \overset{F}{\rightarrow} \underset{F( \_ )}{ \{ \;\;\;\;\; \} } $}, we can return to examine the functor {$ L $}.

{$ \{ \{ A \rightarrow \_ \} \rightarrow ( \_ \overset{F}{\rightarrow} \underset{F( \_ )}{ \{ \;\;\;\;\; \} }) \} $}

I believe that this top down approach is removing a major obstacle that I have had in trying to understand the Yoneda lemma these many years. The functor {$ L $}, as written above, references an object {$ A $} and an object {$ F $}. And the Wikipedia article on the Yoneda lemma says that this is part of an isomorphism that is natural in terms of {$ A $} and {$ F $}. But I think, truly, the isomorphism must be understood in terms of morphism. I need to interpret {$ A $} and {$ F $} in terms of morphisms.

I think my challenge now is to understand {$ \{ A \rightarrow \_ \} $} in a new way, without the {$ A $}, but instead with a morphism {$ f:X \rightarrow Y $}. In my previous post, I was able to do away with {$ F(A) $} and instead work with {$ G(X) \overset{G(f)}{\rightarrow} G(Y) $} and {$ H(X) \overset{H(f)}{\rightarrow} H(Y) $}. Similarly, in this post, I succeeded in doing away with the {$ F $} in {$ ( \_ \overset{F}{\rightarrow} \underset{F( \_ )}{ \{ \;\;\;\;\; \} }) \} $} and working instead with {$ \alpha : G \rightarrow H $}. Therefore, in my next post, I will focus on rethinking the functor {$ \{ A \rightarrow \_ \} $}.

Today I avoided looking at the literature because I wanted to see if this all comes together for me on its own. I didn't want to simply take things as stated without developing my own thoughts. But I think I will switch some gears.

I will note some conclusions that I drew today, which may or may not prove false. One conclusion is that both sides of the isomorphism should say something very basic about natural transformations. Certainly, the right hand side does. The left hand side apparently relates it to the way diagrams of arrows are fit together. I expect that a key idea is that natural transformations are not functors, but rather, are sets of morphisms, and thus leaks out of the purely categorical world. Similarly, the input of a set function is an object, and not a full fledged morphism, and so it likewise leaks out of the purely categorical. Yes, you can define a function on morphisms, but those morphisms must then be thought of as objects. Qualitatively, functions are not functors.

Robert Harper:

I find it helpful to consider a degenerate form of the Yoneda Lemma, for pre-orders, in which case it says that {$x\leq y$} iff {$(\forall z)\, z\leq x \Rightarrow z\leq y.$} From left to right use transitivity of the preorder; from right to left, instantiate z to x, and use reflexivity. The full form of the Lemma is a generalization of this simple, but surprisingly useful, observation.

Robert, Wow! That's fantastic. I like how the instantiation z to x becomes so key. Thank you so much for responding. I did the right thing by posting here.

I add a link to the Wikipedia article on preorders. I recall that preorders came up as a great example in the course on applied category theory, specifically in discussing adjunctions.

I also note that the role of quantifiers becomes apparent. There is the universal quantifiers. But also, I imagine that there is the existential quantifier, in that there exists a z such that z=x. I imagine these two quantifiers get paired up.

The quantifiers are very important for me because they come up when I think of Why as knowledge of Everything, How as knowledge of Nothing, What as knowledge of Something, Whether as knowledge of Nothing. They also come up in the logical square which relates these. But I think I will write about that later. Also, I will want to understand and master how the existential and universal quantifiers are related as adjoint functors. And I will want to understand the Arithmetic Hierarchy, and in particular, the Yates Index Theorem and what it says about the triple jump.

Eduardo Ochs alerted me to Emily Reihl's wonderful, free book Category Theory in Context. I think she has written exactly the book that I want and need. Also, Eduardo sent me his most recent slides. He has his own perspective and I will learn a lot from him.

Yet I will try now further on my own. I have, however, gone back to this comment by Nex at Math Stack Exchange which I find most helpful. He described the two functors {$ R $} and {$ L $} thusly:

{$ R $} is {$ ((α,f):(F,A)→(F′,A′))↦(x↦α_{A′}(F(f)(x))) $} and the objects are mapped {$ (F,A)↦F(A) $}

{$ L $} is {$ ((α,f):(F,A)→(F′,A′))↦(θ↦(α⋅θ⋅\textrm{Hom}(f,−))) $} and the objects are mapped {$ (F,A)↦\textrm{Nat}(\textrm{Hom}(A,−),F) $}

I previously used his expression for {$ R $} and now I will make sense of his expression for {$ L $}, continuing my thoughts above.

I consider again the functor {$ L $}.

{$ \{ \{ A \rightarrow \_ \} \rightarrow ( \_ \overset{F}{\rightarrow} \underset{F( \_ )}{ \{ \;\;\;\;\; \} }) \} $}

It is an object in the functor category {$ \mathbf{Set}^{\mathbf{Set}^C \times C} $} As a functor, it takes a morphism {$ ( \alpha, f) $} in {$ \mathbf{Set}^C \times C $} to a set function {$ \psi $} in {$ \mathbf{Set} $}. Here {$ \alpha : G \rightarrow H $} is a morphism (a natural transformation) in {$ \mathbf{Set}^C $} and {$ f: X \rightarrow Y $} is a morphism in {$ C $}.

What are the domain and the codomain of the set function {$ \psi $} ? They are sets of natural transformations. These natural transformations are morphisms in the functor category {$ \mathbf{Set}^C $}. {$ \psi $} depends on the morphisms {$ \alpha :G\rightarrow H $} and {$ f:X\rightarrow Y $} and so do its domain and codomain. The domain of {$ \psi $} is the set of natural transformations from {$ \{ X \rightarrow \_ \} $} to {$ \_ \overset{G}{\rightarrow} \underset{G( \_ )}{ \{ \;\;\;\;\; \} } $}. The codomain of {$ \psi $} is the set of natural transformations from {$ \{ Y \rightarrow \_ \} $} to {$ \_ \overset{H}{\rightarrow} \underset{H( \_ )}{ \{ \;\;\;\;\; \} } $}.

Let {$ \theta $} be an element in the set of natural transformations from {$ \{ X \rightarrow \_ \} $} to {$ \_ \overset{G}{\rightarrow} \underset{G( \_ )}{ \{ \;\;\;\;\; \} } $}. Then {$ \psi(\theta) $} is an element in the set of natural transformations from {$ \{ Y \rightarrow \_ \} $} to {$ \_ \overset{H}{\rightarrow} \underset{H( \_ )}{ \{ \;\;\;\;\; \} } $}. How do we calculate {$ \psi(\theta) $} ?

{$ \psi(\theta) $} is a natural transformation which takes us from the functor {$ \{ Y \rightarrow \_ \} $} to the functor {$ \_ \overset{H}{\rightarrow} \underset{H( \_ )}{ \{ \;\;\;\;\; \} } $}. But which such natural transformation is it? What distinguishes natural transformations? Natural transformations are distinguished by their components, in this case, {$ \{ \psi(\theta)_A | A \textrm{ is an object in } C \} $}. The components {$ \{ \psi(\theta)_A \} $} are morphisms in {$ \mathbf{Set} $} (they are set functions) which are indexed by the objects in {$ C $}. Moreover, these components should depend on {$ \alpha :G\rightarrow H $} and {$ f:X\rightarrow Y $}.

Given a morphism {$ h:A\rightarrow B $} in {$ C $}, the components of the natural transformation {$ \psi (\theta) $} satisfy the following commutative diagram:

{$ \matrix{ \{ Y \rightarrow A \} & \overset{\psi(\theta)_A}{\longrightarrow} & H(A) \cr \downarrow{\scriptsize \{Y \rightarrow h \}} & & \downarrow {\scriptsize H(h)} \cr \{ Y \rightarrow B \} & \overset{\psi(\theta)_B}{\longrightarrow} & H(B) \cr } $}

The four corners are all sets, and the four sides are all set functions. If {$ m \in \{Y \rightarrow A \} $}, then {$ \{ Y \rightarrow h \}(m) = hm $}. I have written this composition so that, from right to left, first {$ m $} acts, and then {$ h $} acts. If we like, we can now write {$ Y \overset{m}{\rightarrow} A \overset{h}{\rightarrow} B = Y \overset{hm}{\rightarrow} B $}. Our commutative diagram indicates that:

{$ \matrix{ m & \overset{\psi(\theta)_A}{\longrightarrow} & \psi(\theta)_A(m) \cr \downarrow{\scriptsize \{Y \rightarrow h \}} & & \downarrow {\scriptsize H(h)} \cr hm & \overset{\psi(\theta)_B}{\longrightarrow} & \psi(\theta)_B(hm)=H(h)\psi(\theta)_A(m) \cr } $}

{$ \psi (\theta) $} is a natural transformation from {$ \{ Y \rightarrow \_ \} $} to {$ \_ \overset{H}{\rightarrow} \underset{H( \_ )}{ \{ \;\;\;\;\; \} } $} if and only if {$ \psi(\theta)_B(hm)=H(h)\psi(\theta)_A(m) $} for every expression {$ Y \overset{m}{\rightarrow} A \overset{h}{\rightarrow} B $} in {$ C $}.

Recall that the set function {$ \psi $}, the functor {$ H $} and the object {$ Y $} all depend on the input {$ (\alpha : G \rightarrow H, f:X \rightarrow Y) $}. Thus, for possible insight and clarity, I can restate this:

{$ \psi (\theta) $} is a natural transformation from {$ \{ Y \rightarrow \_ \} $} to {$ \_ \overset{H}{\rightarrow} \underset{H( \_ )}{ \{ \;\;\;\;\; \} } $} if and only if {$ \psi(\theta)_B(hm)=H(h)\psi(\theta)_A(m) $} for every expression {$ X \overset{f}{\rightarrow} Y \overset{m}{\rightarrow} A \overset{h}{\rightarrow} B $} in {$ C $}.

I also remind myself that {$ \psi $} is a set function whereas its input {$ \theta $} and its output {$ \psi (\theta) $} are natural transformations, and as such, elements of the respective sets of natural transformations.

I am trying to define {$ L(\alpha, f)=\psi $}. A crucial point is understanding how to distinguish two natural transformations, say {$ \psi (\theta_1) $} and {$ \psi (\theta_2) $}. When are they the same and when are they different? I think this is the crucial part of the Yoneda lemma. So I will write about this in a separate post.

Suppose that {$ \psi (\theta_1) $} and {$ \psi (\theta_2) $} are natural transformations that satisfy the following commutative diagram, where {$\theta = \theta_1 $} or {$\theta = \theta_2 $}.

Note that {$ H $} is given, as part of {$ \alpha: G \rightarrow H $}, and likewise {$ Y $} is given as it comes from {$ f:X \rightarrow Y $}. Whereas {$ h:A \rightarrow B $} could be any morphism in {$ C $}.

How do we know if {$ \psi (\theta_1) $} and {$ \psi (\theta_2) $} are the same natural transformation or two different ones? They are different if they differ on at least one component, and otherwise they are the same. Thus:

{$ \psi(\theta_1) \neq \psi(\theta_2) $}

{$ \iff \exists hm \equiv Y \overset{m}{\rightarrow} A \overset{h}{\rightarrow} B $} such that {$ H(h)\psi(\theta_1)_A(m) \neq H(h)\psi(\theta_2)_A(m) $}

{$ \iff \exists hm \equiv Y \overset{\textrm{id}_Y}{\rightarrow} Y \overset{m}{\rightarrow} A \overset{h}{\rightarrow} B $} such that {$ H(h)\psi(\theta_1)_A(m) \neq H(h)\psi(\theta_2)_A(m) $}

{$ \iff \exists hm \equiv Y \overset{\textrm{id}_Y}{\rightarrow} Y \overset{m}{\rightarrow} A \overset{h}{\rightarrow} B $} such that {$ H(mh)\psi(\theta_1)_Y(\textrm{id}_Y) \neq H(mh)\psi(\theta_2)_Y(\textrm{id}_Y) $}

{$ \iff \psi(\theta_1)_Y(\textrm{id}_Y) \neq \psi(\theta_2)_Y(\textrm{id}_Y) $}

I will draw conclusions in my next post.

I worked for several days with pen and paper. I made incremental progress. Finally, yesterday, I drew a picture which gave me the idea that I was looking for to understand the natural isomorphism described by the Yoneda lemma. This is my understanding, in a single sentence:

The Yoneda Lemma is the Fundamental Theorem of Computation, namely: The validity of a computation is basically the same whether it is run as a self-standing program or as one step in a larger program.

I will try to explain all that I mean by that and explore that further. But first I want to document how I got to this point.

In my series of posts, I felt that I got an understanding of the functor {$ R = F(A) = A \overset{F}{\rightarrow}\underset{F(A)}{ \{ \;\;\;\;\; \} } $}, and so I next turned to the functor {$ L = \textrm{Hom}(\textrm{Hom}(A,–),F) = \{ \{ A \rightarrow \_ \} \rightarrow ( \_ \overset{F}{\rightarrow} \underset{F( \_ )}{ \{ \;\;\;\;\; \} }) \} $}. Each of these functors takes an input {$ (\alpha, f) $} and outputs a set function. In the case of {$ L $}, I was trying to understand this set function {$ \psi: \theta \rightarrow \psi(\theta) $} which maps the natural transformation {$ \theta $} to the natural transformation {$ \psi (\theta) $}. I looked to see what I could learn from the commutative diagram of any component. I was able to show that for any two such natural transformations:

{$ \psi(\theta_1) \neq \psi(\theta_2) \iff \psi(\theta_1)_Y(\textrm{id}_Y) \neq \psi(\theta_2)_Y(\textrm{id}_Y) $}

This made use of a nice reindexing, where I could switch from index {$A $} to index {$ Y $}. But this wasn't enough for me to figure out what the set function {$ \psi $} should be. I realized that I had gone as far as I could on my own. I should work with the formula that Nex at Math Stack Exchange provided, namely {$ θ↦(α⋅θ⋅\textrm{Hom}(f,−)) $}. But first I should read more about the Yoneda lemma.

I read Emily Reihl's exposition in her wonderful book [Category Theory in Context](http://www.math.jhu.edu/~eriehl/context.pdf). It's just the book for me and I hope to learn from her about Kan extensions, which seem to relate to my notion of "extending the domain of a function". She gave a very informative example, the ordinal category {$ \mathbb{\omega} $}, helpful for thinking about the Yoneda lemma. In this category, the morphisms are all compositions of the identity morphisms and the unique morphisms from object {$ n $} to object {$ n+1 $}. Consequently, the functor {$ \mathbb{\omega}(k,\_) $} maps each ordinal {$ n $} to a hom-set that is empty if {$ n<k $} and otherwise is a singleton. This is perhaps the simplest nontrivial example to consider. A natural transformation {$ \alpha $} to some other functor {$ F $} will then be determined by where it sends the identity morphism {$ \textrm{id}_k $} because then {$ F $} determines the rest, by induction.

I worked through her exposition of the Yoneda lemma and her proof of the bijection, making a diagram for each line. She is not wordy but she still explains the lemma in full detail, taking a few pages for that, not reducing it all to one line. But I did not understand her proof of the natural isomorphism. I felt at that point that it would be better for me to try to work with Nex's formula.

I made the diagram below.

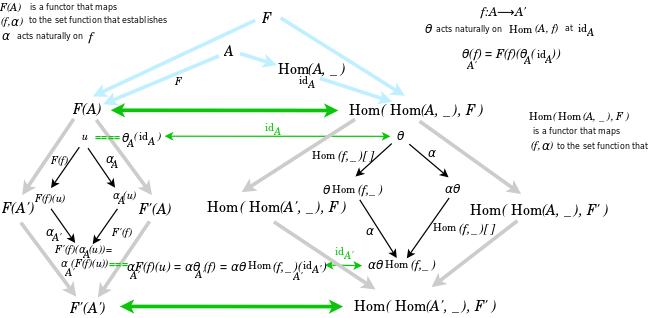
The diagram helped me to appreciate that for the natural isomorphism, given {$ f:A \rightarrow A' $} , we have to think about both

{$ \mathrm{id}_A $} and

{$ \mathrm{id}_{A'} $}.

In particular, the relevant component of the natural transformation {$ \alpha \theta \mathrm{Hom}(f, \_) $} is indexed by {$ A' $} , and indeed we have vertical composition of natural transformations

{$ ( \alpha \theta \mathrm{Hom}(f, \_) )_{A'} $}

{$= \alpha_{A'} \theta_{A'} \mathrm{Hom}(f, \_)_{A'} $}.

I also spent time making sense of the natural transformations {$ \mathrm{Hom}(f,\_): \mathrm{Hom}(A', \_ ) \rightarrow \mathrm{Hom}(A, \_ ) $} and {$ \mathrm{Hom}(\_ , f): \mathrm{Hom}(A, \_ ) \rightarrow \mathrm{Hom}(A' , \_ ) $} , which go in opposite directions.

I drew the diagram thinking that the one step from {$ F(A) $} to {$ F'(A') $} could somehow be matched with three steps from

{$ F(A) $} to {$ \mathrm{Hom}(\mathrm{Hom}(A,\_),F)) $} to {$ \mathrm{Hom}(\mathrm{Hom}(A',\_),F')) $}

Which is to say, the functor {$ \mathrm{Hom}(f,\_) $} was working like a backwards step.

I wanted to understand the the functor {$ L $} as outputting a set function that was expressing something meaningful about natural transformations, as I had done for {$ R $}. Clearly, the desired set function was taking a natural transformation {$ \theta $} defined with regard to {$ (F, A) $} and leveraging and expanding that natural transformation so that it worked as a natural transformation in a new context with regard to {$ (F', A') $}. It was doing that both on the outside, with {$ \alpha $}, and on the inside, in the reverse direction, with {$ \mathrm{Hom}(f,\_) $}. It was doing both sides in parallel, indeed, maintaing the parallelism. It was relating the original pair {$ (\alpha, f) $} with any pair {$ (\theta, g) $} But what could that mean?

I had noticed, while reading Riehl's book and thinking about her subsequent applications, that the identity morphism was better thought of, philosophically or cognitively, as the action of "doing nothing". And I thought that the set function produced by the commutativity diagram of a natural transformation could be thought of as verifying and validating that natural transformation as a computation. My emphasis on morphisms made me think more and more that if everything here is an action, then these are some kind of computations. And that the Yoneda lemma explains precisely the circumstances why and how objects become important.

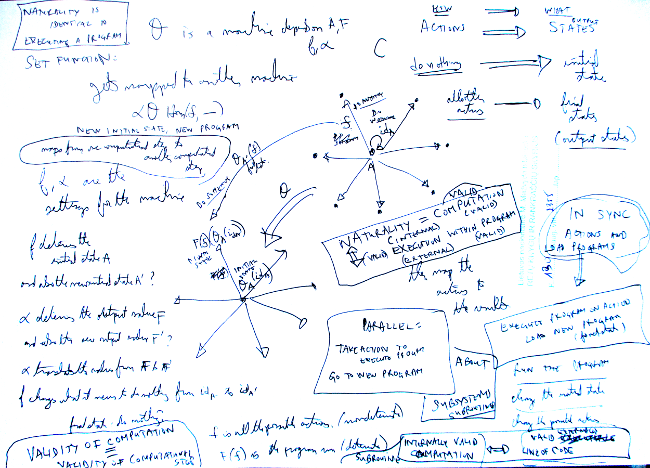
Finally, I drew the picture above of how a homset {$ \mathrm{Hom}(A,\_) $} gets mapped into another category such as {$ \mathbf{Set} $}. It made clear to me the parallelism, that actions in {$ \mathrm{Hom}(A,\_) $} were being mirrored by {$ F $} in {$ D = \mathbf{Set} $}. In both domains we had a clear starting point, a root that everything proceeded from. The difference was that in {$ C $}, that is, locally, in {$ \mathrm{Hom}(A,\_) $}, it was a distinguished morphism, the identity morphism {$ \mathrm{id}_A $}, which got mapped to some distinguished object. But all the other actions in {$ C $} got mapped to objects. Thus in {$ D $} we were thereby distinguishing one initial state and many final states. The states aren't relevant in {$ C $}, but they become relevant in {$ D $} . In {$ C $}, we "do nothing" or we "do something", whereas in {$ D $}, we have initial states and final states.

With this mindset, I realized that the functor {$ L $} was assuring that what worked at {$ (F, A) $} would also work at {$ (F', A') $}. It was describing a step in a program, how it is executed. Now, thinking about that, the restriction to {$ \mathrm{Hom}(A, \_) $} is a restriction to a single step in {$ C $}. Also, what {$ F $} is doing is taking a calculation in {$ C $} and mapping it to some output in {$ D $}. Thus we can consider a program {$ F $} running in its entirety in {$ C $}, or we can break it down, step-by-step, state-to-state, tracking its outputs in {$ D $}. These were the ideas that came up as I started thinking this through and chasing down the meaning. But I will write about this separately.

Clearly, this way of thinking about the Yoneda lemma is very relevant for my goal of distinguishing between Whether, What, How and Why. For example, the calculations in {$ C $} are How and the outputs in {$ D $} are What. Also, this may yield a nice framework for studying computability and so is very promising for my project to understand the Yates Index Theorem.

I thought I should check to see how original this perspective is and so I googled on "Yoneda lemma subroutine" because basically I am saying that the Yoneda lemma is the foundation for subroutines. I came up with some nice links that I will want to study:

Continuation passing style. They say that CPS transform is conceptually a Yoneda embedding.

Math Stack Exchange: Basic example of Yoneda lemma. This mentions subroutines.

What You Needa Know about Yoneda. Profunctor Optics and the Yoneda Lemma. (Functional Pearl). Guillaume Boisseau, Jeremy Gibbons. They mention the preorder example that Robert Harper gave and call it "proofs by indirect equality".

Category theory notes 16: Yoneda lemma (Part 3). Linguist Chenchen (Julio) Song works through the details in his own way, much as I am.

Bartosz Milewski. The Yoneda Lemma.

Now that I have arrived at my main idea, I will try to think it through and write it up from first principles.

Saturday, I wrote a letter to Eduardo Ochs summarizing my interpretation of the Yoneda Lemma. I share that here. This week I hope to share more ideas that came up. Then I will try to write out my interpretation from first principles.

I worked on the Yoneda Lemma almost every day for two weeks, making slow but steady progress every day. Finally, yesterday, I found the idea that I was looking for. It has to do with the Yoneda Lemma as a natural isomorphism in F and A, not just a bijection.

In my understanding, the Yoneda Lemma is the Fundamental Theorem of Computation. It is the mathematical expression of the following basic idea about computation: The validity of a computation is basically the same whether it is a self-standing program or whether it is one step in a larger program.

Here are the underlying ideas:

If we stay within a category C, then all that matters are the morphisms, because the identity morphism can take the place of the associated object.
And within a category C, we can think of the morphisms as possible actions that we can take.
There are two kinds of morphisms: those that do nothing (identity morphisms) and those that do something (all the rest).
A functor F:C->D takes us outside of our category. It is a program that takes actions in C and yields outputs in D.
Here the D could be Set, but it's not yet clear to me how important that is, whether it could be List or something else.
In order to run a morphism in C as a program we need two functors working in parallel. One functor F expresses the execution of the program and the other functor G expresses the output.
A natural transformation is then the validation that the two functors F and G successfully work in parallel.
The states of the program are the objects in D.
Thus the action taken in C - which is a morphism that may be composed of a long path of actions - is implemented as a program in D which expreses such actions as changes in state and thus makes it possible to explicitly break down a program into steps and also separate its execution (the evolution of its internal states) and its possible outputs (its likewise evolving external states).

The Yoneda Lemma is a natural isomorphism between two functors, {$F(A)$} and {$Hom(Hom(A, \_ ), F)$}.

The functor {$( F(A) )$} takes, as it inputs, a natural transformation {$n:F\rightarrow G$} and a functor {$f:A\rightarrow B$}, and outputs a set function. That set function happens to be the one that validates that n is a natural transformation at f. Which is to say, it validates that a program makes sense on its own.

The functor {$( Hom(Hom(A, \_ ) , F) )$} likewise takes, as its inputs, a natural transformation n:F->G and a functor f:A->B, and outputs a set function. That set function maps natural transformations in {$( Hom(Hom(A, \_ ), F) )$} to natural transformations in {$( Hom(Hom(B, \_ ), G) )$}. Specifically, that set function takes an input, the natural transformation m, and outputs the natural transformation {$( nmHom(f, \_ ) )$} , which extends and leverages m so that it works in the new state. So here we are explicitly moving from a valid state (A,F) to valid state (B,G). Here we are saying that the computation is valid because it takes us from a state (A,F), where it works, to a state (B,G), where it works. Mathematically, the key idea is that the "do nothing" action id_A gets mapped to whatever "initial state" object in F(A) and all of the other "do something" actions in Hom(A,_ ) get mapped to "final state" objects in F(A). Then you get to a new valid state: f has taken you to B, and the old program F, which has been run, is now thought of as the new program G. And B has its own "do nothing" action id_B which becomes the "initial state" in G(B). In summary, the functor Hom(Hom(A, _ ), F) outputs a set function on natural transformations which is precisely the one that validates that we can keep going from initial state to initial state, step by step, as we run our program.

The upshot is that the functor F(A) doesn't identify any particular initial state but simply runs and validates all possible computations. And you don't have the concept of breaking down a program into steps or subroutines. Whereas the functor Hom(Hom(A, _ ), F) explicitly frames a single step as a subroutine in some conceivably larger program, and so moves us from an initial state to a final state, which becomes a new initial state. The Yoneda lemma is the machinery that shows that the validity is the same.

This is still murky but I feel that I have grasped the main idea and just need to keep fleshing it out. The idea leapt out yesterday when I drew a picture of the Hom(A,_ ) arrows in C, including id_A, and the related arrows in F(C), including the "initial state" that id_A gets mapped to.

As I work on this, it will become clearer how it relates to Whether, What, How, Why. But, for example, the distinction between the execution (How) and the output (What) seems very important. Also, with natural transformations, there is a distinction between the objects in C, used as indices of the components, and the diagram itself, which is entirely in D. I think C expresses How and D express What.

I am grateful for our interactions. That's what got me to try again with the Yoneda lemma. Yet there is a long way to go. But this is progressing in a promising direction for me because I wanted to relate the Yoneda lemma to computability theory, especially the jump hierarchy and the Yates index theorem (which I think basically says that the third jump has complete knowledge of the zeroth jump).

I later added this thought: From the step-by-step point of view, we can think of a natural transformation F->G as splitting a morphism=computation f in C into two perspectives: the execution F(f) and the outcomes G(f).

Before I start working out the details, from first principles, of my interpretation of the Yoneda Lemma, I want to share some related ideas that have come up these last few days. They are speculative but I think helpful in understanding what to look out for.

Quanta magazine has published a series of interesting articles about the https://www.quantamagazine.org/search?q[s]=universality | universality principle in statistics, and also the Tracy-Widom distribution including this short video. I happened to learn about this just after my interpretation of the Yoneda lemma. I will explain the possible link that I perceive between the two.

The Yoneda Lemma establishes a natural isomorphism which says that we can look at functors from a category {$( C )$} to {$( \mathbf{Set} )$} in two different ways. In my understanding, on the one hand, we can think of them as a calculation taking place in its own system, in which case we just look at the network of morphisms. On the other hand, we can think of them as a calculation taking place within a subsystem of a larger system, in which case we need to have initial states and final states, which is to say, we need to have objects.

What is the value of having two points of view when they are naturally isomorphic? Well, apparently, those different points of view can matter, as follows. From the network of morphisms point of view, the network grows as {$( n^2 )$}, whereas from the systems and subsystems of objects point of view, the network grows as {$( n )$}. Simply put, the number of possible binary relationships is quadratic to the number of states or nodes or objects. So as a system grows, it can be burdensome to maintain the quadratic growth, and if at all possible, one might shift perspectives to express the same system in terms of linear growth. Which is to say, if we have a cost to our perspectives, then we may shift them, yielding a phase transition. This is to say that the two points of view may have real implications. In other words, they may be real. Of course, cognitively, they are real, but they may be real not just cognitively. That makes our thinking about these things all the more interesting.

It seems possible that the Tracy-Widom distribution models precisely such a shift. On the one side it goes down {$( e^{-N} )$} and on the other side it goes down {$( e^{-N^2} )$}, and apparently it models this phase transition.

>The asymmetry of the statistical curve reflects the nature of the two phases. Because of mutual interactions between the components, the energy of the system in the strong-coupling phase on the left is proportional to ( N^2 ). Meanwhile, in the weak-coupling phase on the right, the energy depends only on the number of individual components, ( N ). “Whenever you have a strongly coupled phase and a weakly coupled phase, Tracy-Widom is the connecting crossover function between the two phases,” Majumdar said. At the Far Ends of a New Universal Law

Furthermore, the identity morphisms in the Yoneda Lemma could be crucial for such transitions. Imagine a system that is a collection of interrelated actions (arrows) which satisfy a composition law, but without any objects. And imagine that the system keeps growing through the addition of new actions. The burden of keeping track of everything will grow. Now some of those actions may self-compose, which is to say, they may loop upon themselves. And some of those self-looping actions may have no effect on any other actions, upon composition, which is to say, they are identity actions, "do nothing" actions. Then what could happen is that those identity actions could anchor and define a subsystem. What does such a definition mean? It means that a phase transition takes place, where many of those identity actions, and all the related actions, may form a coherent subsystem, disjoint from the main system, that can "drop out" of it. And their dropping out is simply a matter of a shift in perspective. They can still be thought of as in the main system, but they can also be thought of as a self-standing subsystem which is incorporated into the main system, and they can also be thought of as their very own system. The Yoneda Lemma, in my interpretation, is the framework that allows for these shifts and ambiguities in perspective.

Which is to say, the Yoneda Lemma may be precisely the conceptual framework that grounds such a shift in perspective by which a growing system comes to be made up of subsystems.

As I read a bit about random matrices, which is related to this, I saw that such concepts are important in the study of topological insulators. There is a nice series of videos and lecture notes on that, Course on topology in condensed matter. I learned that "zero energy excitations" are crucial in this subject. When there are no such zero energy excitations, then certain systems aren't able to transform into other systems, and thus we get classes of systems. Well, not knowing anything, such "zero energy excitations" bring to mind the "do nothing" actions.

Another physical idea in all of this is that objects and arrows are distinguished in the way that fermions and bosons are. Two objects cannot be in the same place, and the same is true for fermions. But two arrows can be in the same place, and the same is true for bosons. I mean to say that two arrows can start at the same object and end at the same object but be entirely different arrows. So a shift from an "object point of view" to an "arrow point of view" may be like a shift from "fermion statistics" to "boson statistics".

These mathematical connections are very interesting to me because the topological insulators are classified by Bott periodicity, which I think is related to an eight-cycle of conceptual frameworks (divisions of everything) that is central in my philosophy. Also, they relate to Dysons's Threefold Way, symmetry classes of random matrices (complex Hermitian, real symmetric, or quaternion self-dual) that I think relate to the classical Lie groups, which I think are related to the cognitive frameworks that I study, including the foursome: Whether-What-How-Why.

I think the Yoneda Lemma is modeling the relationship between a system and a subsystem. That is an asymmetric relationship and so it involves an asymmetric phase transition. From my studies of the ways of figuring things out in math and physics, there is what happens before we have a system, and what happens once we have a system. And at the crucial point in between, we have in physics the establishment of a subsystem within a system (as with Faraday's pail). And in math, we have a symmetry group. Well, the Yoneda Lemma is a generalization of Cayley's theorem, whereby every group can be thought of as a permutation group. And here we see the alternatives - we can keep track of a group using {$( n \times n )$} matrices, or we can allow it to keep track of itself, however it likes, using its own {$( n )$} elements.

The Tracy-Widom distribution deals with the largest eigenvalue for a random matrix. The universality principle is an apparently related but slightly different matter of the spacing between all of the eigenvalues. I just want to add that such a spacing also seems like a very important matter in emerging systems. In our universe, it is surprising and very important for physicists that the forces in nature have their effects at different orders of magnitude, because otherwise it would be impossible for us to tease them apart and make sense of any of it. Similarly, architect Christopher Alexander, in his 15 principles of life, notes the importance of Levels of Scale, typically of size 3, which are crucial so that we have gaps between the levels. Apparently, these could be mechanisms for assuring such gaps in levels of scale.

I want to conclude with the following idea from Silicon Valley on the value of networks. A single fax machine is worthless. It becomes valuable when there is a second fax machine. And with each new fax machine, the value of the network grows by that machine's possible relations with all the other machines. Which is to say, the value of the network grows quadratically. Of course, the flipside is that the cost of a network can grow quadratically, and that can drive the appearance of subsystems within the system.

Certainly, these are all speculative ideas, but they are important for me to mull as I try to master Yoneda's Lemma.

Perhaps somebody has thoughts or comments?