Math 4 Wisdom. "Mathematics for Wisdom" by Andrius Kulikauskas.

Math, Math concepts, Theorems, Math constants, Abstraction, Math discovery, The purpose of math

数学地图

Currently working here: Math Companion

Create a map that show how the branches of math unfold to yield its key concepts and results.

Collect and organize mathematical results.
Study the history of how math grows.
Document the ways and results of abstraction.
Express the link between algebra and analysis in terms of exact sequences and Kan extensions.
Explain why category theory not relevant for analysis.

Elements of the map of mathematics

The map of mathematics should include:

Branches of math
Objects, concepts
Constants, functions, equations ?
Challenges (questions) and theorems (answers)
Ways of figuring things out and methods of proof

A House of Knowledge for each branch of mathematics

There is a house of knowledge for mathematics overall. Moreover, every science, and in particular, every branch of mathematics should have its own house of knowledge. Thus the map of mathematics should explain how all of these houses of knowledge are related, how they arise and unfold.

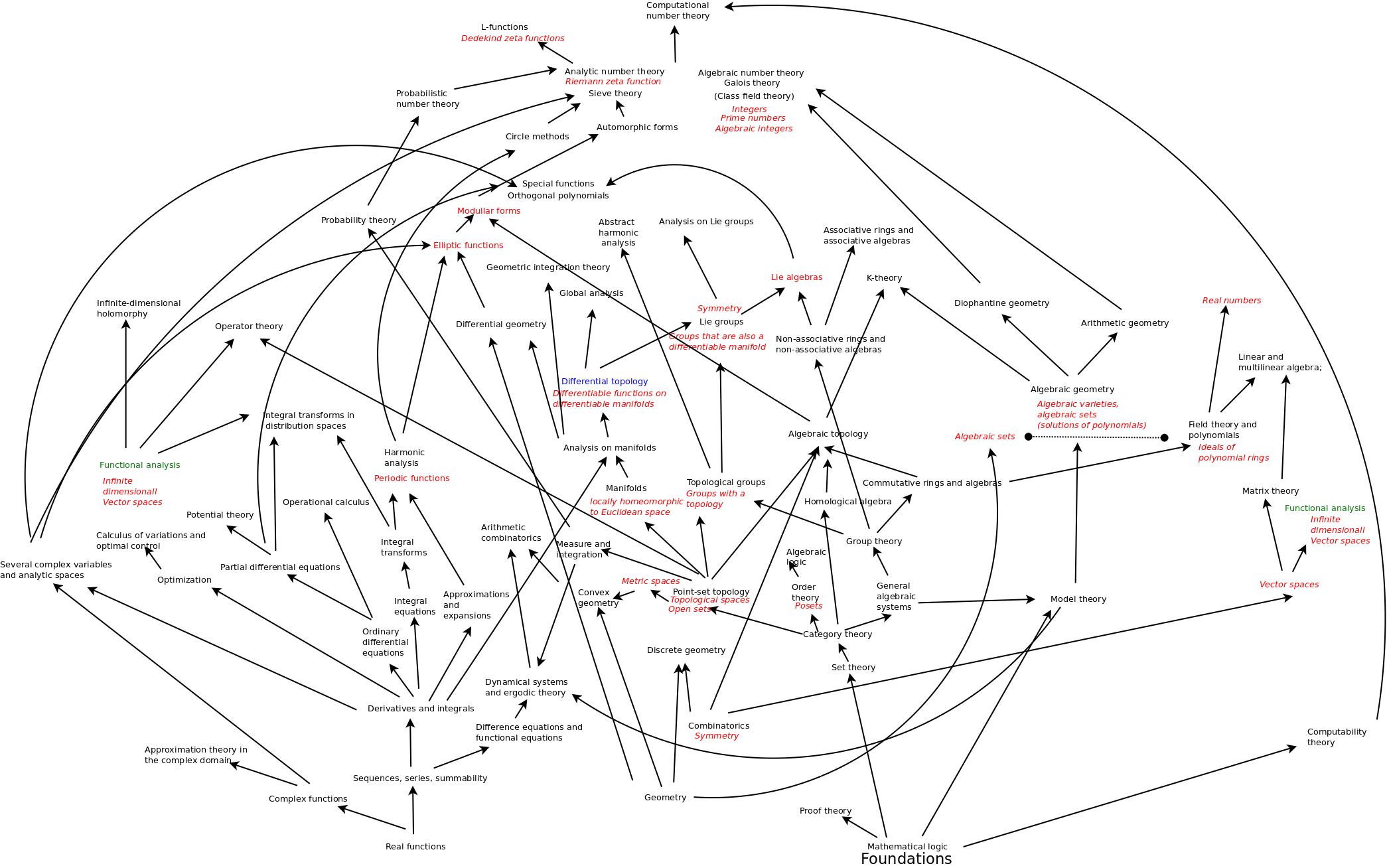
Earlier investigations

I made the map above based on the Mathematics Subject Classification. Arrows show my understanding of how areas depend on each other.

Readings

The Princeton Companion to Mathematics Online
Quanta magazine. Map of mathematics.
Mathematics: Form and Function (wikipedia has list of human activities) by Saunders Mac Lane
Mathematics: Its Content, Methods and Meaning, Volume 1, Volume 2, Volume 3 by Aleksandrov, Kolmogorov, Lavrentev

Notes

Mathematics Subject Classification wiki
Combinatorics. The mathematics of counting (and generating) objects. I think of this as the basement of mathematics, which is why I studied it.
Algebra is thinking step-by-step (with the conscious hemisphere). So algebra is temporal. Whereas geometry is spatial - it deals with the whole (with the unconscious hemisphere). And what does analysis mean here?
Attiyah: Number theory (Connes - noncommutative algebra) is linked by Geometry (Penrose - twistors) to Physics (Witten - strings).
https://www.researchgate.net/post/What-is-required-of-a-system-of-mathematical-objects-and-structures-to-be-called-a-geometry
Max Tegmark. Is “the theory of everything” merely the ultimate ensemble theory?

In the unfolding of math

consider math as given by generators and relations
the relations are equivalence classes

I dreamed of the grouping of examples from branches of mathematics by considering whether they involve, for example, aspects of mathematics, logic, semantics, and so on.