- MathNotebook
- MathConcepts
- StudyMath
- Geometry
- Logic
- Bott periodicity
- CategoryTheory
- FieldWithOneElement
- MathDiscovery
- Math Connections
Epistemology
- m a t h 4 w i s d o m - g m a i l
- +370 607 27 665
- My work is in the Public Domain for all to share freely.
- 读物 书 影片 维基百科
Introduction E9F5FC
Questions FFFFC0
Software
See: Math, Classical Lie groups, Tensor, Geometry, SU(2), Exceptional Lie algebras
Universal hyperbolic geometry: Relationships with Lie theory.
- Perpendicularity and the Lie bracket.
- Orthocenters and the Jacobi identity.
- Universal circle (the wall between inside and outside - is it the wall between propagation forwards and reflection back?) and ...?
- Ortho-axis - most important line - and ...?
Think about spectral graph theory. Is it relevant for Dynkin diagrams?
References
Videos to study
- Norman Wildberger: Universal Hyperbolic Geometry
- Gang Xu: Lie groups and Lie algebras
- David Tong: Quantum Field Theory
- Paul Langacker: The Standard Model
- Perimeter Institute search "Lie Algebras"
- Maite Dupuis
- Gang Xu
- Freddy Cachazo
- M.S.Raghunathan. Lie Groups
Writings
- Claudiu Remsing
- Remsing. Lecture notes on matrix groups. Very clear and simple with basic examples.
- Remsing. Geometry. Leads to Lie groups.
- Geometric control Application of Lie theory.
- Richard Borcherds, Mark Haiman, Nicolai Reshetikhin, Vera Serganova, Theo Johnson-Freyd. Part I: Lie Groups. Textbook. Includes spinors and Clifford algebras.
VGTU
- Lectures on Advanced Mathematical Methods for Physicists, Sunil Mukhi and N. Mukunda
Victor Kac: Introduction to Lie Algebras
- Lecture 1 — Basic Definitions (I)
- Lecture 2 — Some Sources of Lie Algebras
- Lecture 3 — Engel’s Theorem
- Lecture 4 — Nilpotent and Solvable Lie Algebras
- Lecture 5 — Lie’s Theorem
- Lecture 6 — Generalized Eigenspaces & Generalized Weight Spaces
- Lecture 7 — Zariski Topology and Regular Elements
- Lecture 8 — Cartan Subalgebra
- Lecture 9 — Chevalley’s Theorem
- Lecture 10 — Trace Form & Cartan’s criterion
- Lecture 11 — The Radical and Semisimple Lie Algebras
- Lecture 12 — Structure Theory of Semisimple Lie Algebras (I)
- Lecture 13 — Structure Theory of Semisimple Lie Algebras II
- Lecture 14 — The Structure of Semisimple Lie Algebras III
- Lecture 15 — Classical (Semi) Simple Lie Algebras and Root Systems
- Lecture 16 — Root Systems and Root Lattices
- Lecture 17 — Cartan Matrices and Dynkin Diagrams
- Lecture 18 — Classification of Dynkin Diagrams
- Lecture 19 — Classification of simple finite dimensional Lie algebras over F
- Lecture 20 — Explicitly constructing Exceptional Lie Algebras
- Lecture 21 — The Weyl Group of a Root System
- Lecture 22 — The Universal Enveloping Algebra
- Lecture 23 — Decomposition of Semisimple Lie Algebras
- Lecture 24 — Finite dimensional g-modules over a Semi-Simple Lie algebra
- Lecture 25 —Dimensions and Characters of Semisimple Lie Algebras
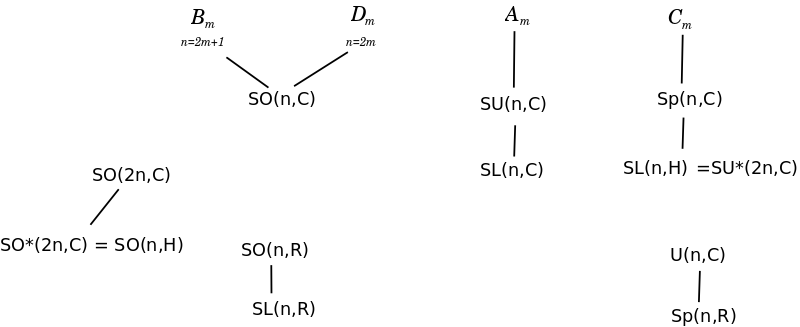
Short texts Classical group: Discussion of forms
- Peter Voit on the most important Lie groups and Lie algebras for physics
- Intuitive explanation for the connection between Lie Groups and projective spaces over R, C, and H
- Wikipedia: Symmetric Spaces and their classification.
- Lie groups and algebraic groups, introductory paper by M.S.Raghunathan, T.N.Venkataramana
- Dynkin Diagrams or Everything You Ever Wanted to Know About Lie Algebras (But Were Too Busy To Ask) Nicolas Rey-Le Lorier
- Intuitive explanation for the connection between Lie Groups and projective spaces over R, C, and H
- Finite Coxeter group properties žiūrėti lentelę
- pradedant tensoriais
- Lie theory through examples
- http://link.springer.com/book/10.1007%2F978-1-4612-0979-9
- Exceptional Lie groups
- Octonions by John Baez
- http://phyweb.lbl.gov/~rncahn/www/liealgebras/texall.pdf
- Group theory, representation theory of Symmetric group
- Symmetric space, including modern classification by Huang and Leung.
- Amplituhedron, post by Jaroslav Trnka related to walks on trees? video
- Root systems: Lie algebrų rūšių pagrindas
- Continuum mechanics
Online books
- I.M.Yaglom. Felix Klein and Sophus Lie : evolution of the idea of symmetry in the Nineteenth Century
- Quantum Theory, Groups and Representations: An Introduction, Peter Woit. Concrete examples. Tensors, symplectic geometry, Clifford algebras and geometry.
Print books
- Knapp. Lie Groups Beyond an Introduction Geometry
- Peskin, Schroder: An Introduction to Quantum Field Theory
- Reviews of Quantum Field Theory books
- From Groups to Geometry and Back
- Matrix Groups for Undergraduates
Lectures
Notes
Root systems
I am studying the possible root systems. They seem to describe the ways of relating two dimensions. A dimension can be considered the simplest root system, with 2 roots, opposite to each other.
Instead of roots, I think we should think of oriented dimensions acting as oriented mirrors, o-mirrors. And we can consider the Weyl chamber with regard to which all such o-mirrors are oriented. Each dimension is perhaps a slot defined by the Lie algebra for a continuous parameter in a Lie group. Thus the Lie algebra explains how the parameters in a Lie group are related with each other.
Each node in a Dynkin diagram is an o-mirror but also each edge in the Dynkin diagram is an o-mirror across which one node is reflected to another. The reflection may be two-directional in the case of a single bond (120 degrees) or one-directional in the case of a double bond (135 degrees) or triple bond (150 degrees).
The Cartan matrix gives the freedom of the root b in the direction of root a, that is the reflective distance between -b and b in terms of a. This distance is positive (2) in the case of a itself, because -a + 2a = a. We can think of this as the measure of increasing freedom inherent in each independent dimension. Otherwise, for b it is negative, either -1, -2, -3. We can think of this as the measure of decreasing freedom because it is the link that relates two dimensions. (Why is this more negative as the span increases?) The determinant of the Cartan matrix needs to be positive because it is a positive definite matrix. This means that the positive freedom (increasing slack) has to be greater than the negative freedom (decreasing slack). This is why the maximum is -3 and -4 is ruled out because the determinant would be 0 = 2*2 - 1*4.
The relationship between two fundamental roots defining two dimensions is given by the number of times one root can be added to the other and still be a root. If the angle is 90 degrees - 0 times, 120 degrees - 1 time, 135 degrees - 2 times, 150 degrees - 3 times. Thus if two dimensions are not directly connected, then they can be considered separated by 90 degrees, but otherwise there are three ways they may be connected.
Two dimensions may not be directly connected but yet be indirectly connected by way of another dimension. The principal way this occurs is through another dimension that is 120 degrees separated from one root and likewise 120 degrees separated from the other root. The other two roots can then be separated from each other by 90 degrees. We may imagine that 120 degrees is the square root of 90 degrees, in this sense. That is why this is not possible for other degrees, because it needs to be symmetrical going in both directions. Thus this is the way that we can have unbounded chains of dimensions, with adjacent dimensions separated by 120 degrees, and all other dimensions separated by 90 degrees. I can try to visualize such a chain by relabeling dimensions, that is, "forgetting" old dimensions and considering them as new dimensions.
So this chain defines the A-series. We can think of it as transmitting a signal. If we start with one-dimension at one end, then the A-series can end in four ways at the other end. These are the classical Lie groups. Also, the one-dimension can lead to a double bond which must end symmetrically, yielding F4. Otherwise, there may be three series coming together into one dimension. These may describe a "coincidence" of three signals coming together. The possible lengths of the series are determined by the equation 1/p + 1/q + 1/r > 1, yielding the D and E series. Finally, two dimensions may be related by a triple bond, yielding G2.
Dynkin diagrams not allowed are those for which the Cartan matrix of a Dynkin subdiagram has determinant zero. This is to say that the Cartan matrix needs to be invertible. I think that if the Cartan matrix for a subdiagram is singular, then it is also for the diagram. One test, in particular, is whether the rows are linearly independent, as they are in the case of a cycle (add all rows and you get 0). The determinant {$d_{n}$} of the Cartan matrix for An (the chain) is given by the recursion formula {$d_{n+1}=2d_{n}-d_{n-1}$}, which is to say, they obey the arithmetic mean {$d_{n}=(d_{n-1}+d_{n+1})/2$}. The initial conditions for An are A0=2 and A1=3 so they continue increasing by 1. The same recursion formula holds if we start our chain with initial conditions B0=2 and B1=2 and then we get that the determinant Bn=2. Similarly, we have C0=2, C1=2, Cn=2 and D0=4, D1=4, Dn=4. Now if we have a B or C type ending at the other end of the chain, then the recursion formula switches to {$d_{z+1}=2d_{z}-2d_{z-1}$} which yields 0 for B, C type endings. Similarly, if we have a D type ending at the other end of the chain, then the recursion formula switches to {$d_{z+1}=4d_{z}-4d_{z-1}$} which yields 0.
If we build up a Dynkin diagram (and Cartan matrix), then a single edge applies the recursion above - if the last two states differ by +1, then so will the next one, and if the last two states are equal, then likewise the next state will be equal. A double edge, if applied as above, will yield 0 if the two states are equal.
For groups the important point is that, where RT is R transpose, R*RT = 1 iff the inner product (and lengths) is preserved. And this is the "shortcut" that makes it possible to take the inverse in the group. So the possible Lie groups are given by the possible inner products.
The Cartan matrix M is DS where S is positive definite because the simple roots span all of Euclidean space. This is not the case when we have a cycle or other configuration where the determinant is 0 and so the whole space is not spanned. By continuity looking at the product of eigenvalues, if one is negative, then in order for it to become positive, it would have to pass zero, which means that the eigenvectors could not have spanned the whole space (?)
The constraints on A-cycles and A-loops are logical but the constraining equations allowing G2 are geometrical based on the possible legs for a right triangle.
Symplectic algebras involve pairs of dimensions - perhaps because the extra root is longer by 2. Whereas the even orthogonal algebras
A classical group is a group that preserves a bilinear or sesquilinear form on finite-dimensional vector spaces over R, C or H. A form {{math|φ: V × V → F}} on some finite-dimensional right vector space over {{math|F {{=}} R, C}}, or {{math|H}} is
- bilinear if: ${\varphi(x\alpha, y\beta) = \alpha\varphi(x, y)\beta, \quad \forall x,y \in V, \forall \alpha,\beta \in F.}$
- sesquilinear if: ${\varphi(x\alpha, y\beta) = \bar{\alpha}\varphi(x, y)\beta, \quad \forall x,y \in V, \forall \alpha,\beta \in F.}$
Metric preserving groups. Groups preserving:
- bilinear symmetric metrics are called orthogonal
- bilinear antisymmetric metrics are called
- sesquilinear metrics are called unitary
- special orthogonal are groups preserving bilinear symmetric metrics and also volumes
- special symplectic are groups preserving bilinear antisymmetric metrics and also volumes
- unitary-symplectic groups are the intersection of U(2N) and Sp(2N) and are isomorphic with unitary groups in a Quaternion space USp(2N) ~ U(N,H)
Sum of epsilon-i equals zero because of the trace. Note that the sum changes size as i grows but it's still zero. It is shifting like the center of the simplex.
Fundamental roots are raising and lowering operators for a root lattice. (You stay within the lattice.)
If you start with the "lowest weight" combination, then you can get Zero and all of the negative roots as well.
There is a lowest maximal weight from we can go back (negatively) to each fundamental root. (?) So a root system is simply the components of the lowest maximal weight (the opposite of zero). This means we have a finite closed system (a building block) for the lattice (similarly to the cube for the usual grid, or other polytopes). When is that true? How does that extend? In each root direction? Bond strength shows the amount of raising and lowering that is possible.
Lattice generated by independent vectors. Not interesting. All the same, get a cube. It's interesting when we get repetition. Lattice generated by independent vectors embedded in a smaller space is more interesting. This is the fundamental task of geometry and likewise of neurons, to economize. How small can the space be? And there is an underlying space epsilon-1, epsilon-2... and how are these spaces related? Measure how much compression there is. They are and must be integers. Consider if we have n*alpha + m*beta = 0, what does that say about theta?
Roots ei - ej are the perspective that opposites coexist. Whereas ei or ei+ej mean it's all the same? And are the classical groups given by a foursome of representations for relating these two perspectives?
Lie Bracket:
- Remiasi tuo, kad summing over permutations of 1 yield 0. [x,x]=0
- Summing over permutations of 2 yields 0. [x,y]+[y,x]=0
- Summing over permutations of 3 yields 0. [x,[y,z]] + [y,[z,x]] + [z,[x,y]]=0
That's true writing out [x,y]=xy-yx and summing out you get a positive and a negative term for each permutation. But also true in the brackets directly permuting cyclically. What would it look like to sum over permutations of 4?
Lie groups and Lie algebras
- ways of breaking up an identity into two elements that are inverses of each other
- orthogonal: symmetric transposes of each other
- unitary: conjugate transposes of each other
- symplectic: antisymmetric transposes of each other
- two out of three property At the level of forms, this can be seen by decomposing a Hermitian form into its real and imaginary parts: the real part is symmetric (orthogonal), and the imaginary part is skew-symmetric (symplectic)—and these are related by the complex structure (which is the compatibility).
Today I watched video "J2 Unitary Groups" from doctorphys series on "Theoretical Physics" at YouTube. https://www.youtube.com/playlist?list=PL54DF0652B30D99A4 I appreciate that he actually calculates some small, concrete examples, which is what I try to do, too. And then he made an extra remark which made things click for me. He explained for a particular matrix that when you take the inverse, it's just like reversing the direction of the angle.
So I want to apply that insight and write up my thoughts on making sense of the classical Lie groups. I will start by describing what they are.
First, I will explain what a "group" is. In math, a group is at work/play whenever we think/talk about actions. For example, imagine a drawing in the plane. Let's establish some point in the drawing where we pin it down to the plane. Then we can rotate that picture by X degrees. Let's say, for the sake of concreteness, that X is an integer from 0 to 359. Then the rotations are "actions" in that they can be:
- added: rotations by X and by Y can be added to get a rotation by X+Y
- it's associative (you can insert parentheses as you prefer): rotating by ((X+Y)+Z) = rotating by (X + (Y+Z))
- there's an action which does nothing, leaves things be, namely the "identity" action 0
- you can undo each action. Rotation by X (say 40 degrees) can be undone by some other rotation (320 degrees = -40 degrees).
We call this a "group" of actions (elements, operators, etc.)
You can have subgroups. So if we restrict ourselves to rotations by multiples of 5 degrees (5, 10, 15...) we will have the 60 rotations we need for the minute hand of an old-fashioned, pre-digital clock. If we restrict ourselves to rotations of 30 degrees (30, 60, 90...) we will have the 12 rotations we need for the hour hand of that same clock. If we restrict to rotations of 90 degrees (0, 90, 180, 270), then we have the 4 rotations which would keep our drawing unchanged if it was a square. This is called a "symmetry group" but the others are symmetry groups, too, for the right objects. If we restrict to rotations of 72 degrees, then we have the 5 rotations that would keep a pentagon unchanged. This last subgroup would be special because it doesn't have any subgroups, partly because 5 is a prime number. Such subgroups are valued as building blocks for more complicated groups.
All of these groups are "commutative" because rotating by X and by Y is the same as rotating by Y and then by X. But there are groups which are not commutative. Let's take the 4 rotations (0, 90, 180, 270) of the square in the plane and let's add a reflection R that flips the square over on that plane. Then it turns out that we have a group of 8 actions and we have, for example, that 90 + R does not equal R + 90. You can imagine non-commutativity is typical when you play with a Rubik's cube (the order of the actions matters).
All of these groups are finite. But we can also have infinite groups. Imagine if we rotated by any real number of degrees. These rotations happen to also be continuous, which is not trivial to make rigorous, but I think basically here boils down to the fact that we can make infinitesimal, that is, itsy bitsy rotations, as small as we want. So then we have a Lie group. You can imagine that Lie groups are important in physics because we live in a world where actions can be subtle and continuous.
The "building blocks" of the Lie groups have been classified. There are four families of groups, An, Bn, Cn, Dn, where n is any natural number. These are called the classical Lie groups. There are also five exceptional Lie groups. I would like to intuitively, qualitatively understand the essence of those classical groups, so I could feel what makes them different and what they share in common. I have failed to find any such exposition.
But I think I'm getting closer. These classical Lie groups are known as the unitary (An), orthogonal (odd and even, Bn and Dn) and symplectic (Cn). These can all be thought of as groups of matrices. Each matrix can be thought of as an action, as a rule which tells you how to break up one vector into components, modify those components, and then output a new vector. These rules can be composed just like actions. In general, matrices and matrix multiplication are used to describe explicitly a group's actions and how they are composed. This is called a group representation. It's a bit like writing down the multiplication table of a group. Mathematicians study the restrictions on the types of tables possible and can determine from that the nature of the group, for example, how it breaks down into subgroups.
The numbers in these matrices can be complex numbers. Now for me the key distinction seems to be that in each group there is a special way to imagine how an action is undone. In other words, there is a special relation between a matrix and its inverse. You undo an action:
- in a unitary group, by taking the conjugate transpose of its matrix.
- in an orthogonal group, by taking the symmetric transpose of its matrix.
- in a symplectic group, by taking the anti-symmetric transpose of its matrix.
What is a transpose? An NxN matrix is a set of rules which takes a column vector (of N components) as the input and outputs a row vector (of N components). Then the transpose is the same set of rules but just reorganized so that the input is a row vector and the matrix outputs a column vector. That will be important if we think in terms of tensors where the row vectors and the column vectors are the extremes of top-down thinking and bottom-up thinking in building a coordinate space. So this is what the classical Lie groups all have in common.
Where they differ is on how they modify the transpose so that the group's action is undone.
Joe, Kirby,
I'm thinking that this distinction between ratios and products comes up as the distinction between "contravariants" and "covariants". And I'm imagining that a (p,q) tensor tells you that p dimensions are to be understood in terms of "division" (contravariants, as with vectors) and q dimensions are to be understood in terms of "multiplication" (covariants, as with covectors - reflections). I'm still trying to figure it out. For example, if you have an answer A = 5 / 7 then on the one hand you are dividing, and in fact, the denominator 1/7 is the "unit", that is, the "denominated" whereas the 5 is the amount, the "numerated". If you want the fraction to stay the same then you have to multiply the top and bottom by the same. I mean to say that I don't understand but I think that tensors are relevant to this question.
The link between difference/sum and ratio/product is given by the exponential/logarithm function. In particular, the Lie group G and the Lie algebra A are related by:
e**A = G
So this is a key equation for relating the discrete world (Lie algebra A) and the continuous world (Lie group G). Addition/subtraction in the discrete world is matched by multiplication/division in the continuous world.
The equation above involves matrices. In general, there is the very meaningful "polar decomposition" of matrices:
M = P U = P e**iH analogous to polar coordinates for a complex number: z = R e**i t
P is a positive semi-definite Hermitian matrix, which means that all of its eigenvalues are nonnegative real numbers, which means that the effect of the matrix P is simply to distort the lengths of vectors in various directions (which is analogous to R).
U is a unitary matrix, which means that it preserves lengths but may be a rotation, for example, as given by the Hermitian matrix H, whose eigenvalues are real.
Well, for Lie groups (continuous groups) to exist their actions (their elements) need to have counteractions, that is, inverses. And when those actions are described as matrices, it turns out that there can't be any radial component P. That is, the matrix can't stretch vectors bigger or smaller. Otherwise, apparently, the action would rip the group apart, it would not be continuous. All that can exist is the angular component. In other words, the volumes (bound by a set of vectors) have to be preserved. These volumes are given by the determinant, which I think detects what is "inside" the volume and what is "outside" of it. The determinant has to be nonzero (so that the volume doesn't collapse, and thus the matrix is reversible), but also it has to have absolute value 1 (so that there is no stretching bigger or smaller). We can also relate this to Cramer's rule for calculating the inverse of the matrix, where the denominator is the determinant, and thus in our case there is no denominator to speak of.
What this means is that for Lie groups there is always a "short cut" for calculating the inverse of the action. In the case of the circle group, for example, it means that an action doesn't have to be thought of as a big matrix that needs to be inverted. Instead, in that case we can think of the action as rotating by an angle, and the inverse is simply rotating back. Thus these "short cuts" are given by the adjoint matrix. For example, for unitary matrices the short cut for calculating the inverses is to take the conjugate transpose.
So now I'm trying to understand what "short cuts" are allowed. That apparently classifies the Lie groups. The way that classification is made is instead to look at the Lie algebras. Instead of looking at multiplication (in Lie groups) we look at addition (in Lie algebras). The addition is I think described by crystallographic lattices, which is where the tetrahedral vs. Euclidean geometries come up, for example. And so it is possible to calculate the limited possibilities for the geometry. So I will try to figure that out and report back.
A related way to understand this is to look at the "normal forms" preserved by the Lie groups. I suppose this means that each Lie group preserves not only the lengths (and volumes) but something more precise. There aren't many possibiities, though.
Notes
- Jacobi identity - constraint on nonassociativity - arises from commutator
- anti-commutativity - arises from commutator - relates duality of order of elements with a duality of positive and negative signs
Lie theory
- When do we have all three: orthogonal, unitary, symplectic forms? And in what sense do they relate the preservation of lines, angles, triangular areas? And how do they diverge?
- Signal propagation - expansions. Consider the connection between walks on trees and Dynkin diagrams, where the latter typically have a distinguished node (the root of the tree) from which we can imagine the tree being "perceived". There can also be double or triple perspectives.
- How do special rim hook tableaux (which depend on the behavior of their endpoints) relate to Dynkin diagrams (which also depend on their endpoints)?
- Relate the ways of breaking the duality of counting with the ways of fusing together the sides of a square to get a manifold.
Lie groups
- Homology calculations involve systems of equations. They propagate equalities. Compare this with the determinant of the Cartan matrix of the classical Lie groups, how that propagates equalities. The latter are chains of quadratic equations.
- An grows at both ends, either grows independently, no center, no perspective, affine. Bn, Cn have both ends grow dependently, pairwise, so it is half the freedom. In what sense does Dn grow, does it double the possibilities for growth? And does Dn do that internally by relating xi+xj and xi-xj variously somehow?
- SL(2) - H,X,Y is 3-dimensional (?) but SU(2) - three-cycle + 1 (God) is 4 dimensional. Is there a discrepancy, and why?
- 4 kinds of i: the Pauli matrices and i itself.
- John Baez. From the Octahedron to E8
- Relate harmonic ranges and harmonic pencils to Lie algebras and to the restatement of {$x_i-x_j$} in terms of {$x_i$}.
- In Lie groups, real parameter subgroups (copies of R) are important because they define arcwise connectedness, that we can move from one point (group element) to another continuously. See how this relates to the slack defined by the root system.
- Lie algebra matrix representations code for:
- Sequences - simple roots
- Trees - positive roots
- Networks - all roots
- The nature of Lie groups is given by their forms: Orthogonal have a symmetric form {$\phi(x,y)=\phi(y,x)$}, Unitary have a Hermitian form {$\phi(x,y)=\overline{\phi(y,x)}$}, and Symplectic have an anti-symmetric form {$\phi(x,y)=-\phi(y,x)$}. Note that symmetric forms do not distinguish between {$(x,y)$} and {$(y,x)$}; Hermitian forms ascribe them to two different conjugates (which may be the same if there is no imaginary component); and anti-symmetric forms ascribe one to {$+1$} and the other to {$-1$}, as if distinguishing "correct" and "incorrect".
- Understand how forms relate to geometry, how they ground paths, distances, angles, and oriented areas.
- Understand how forms for Lie groups relate to Lie algebras.
- Understand how forms relate to real, complex and quaternionic numbers.
- Noncommutative polynomial invariants of unitary group.
- Francois Dumas. An introduction to noncommutative polynomial invariants. http://math.univ-bpclermont.fr/~fdumas/fichiers/CIMPA.pdf Symmetric polynomials, Actions of SL2.
- Vesselin Drensky, Elitza Hristova. Noncommutative invariant theory of symplectic and orthogonal groups. https://arxiv.org/abs/1902.04164
- How to relate Lie algebras and groups by way of the Taylor series of the logarithm?
- Consider how A_2 is variously interpreted as a unitary, orthogonal and symplectic structure.
- Look at effect of Lie group's subgroup on a vector. (Shear? Dilation?) and relate to the 6 transformations.
- The complex Lie algebra divine threesome H, X, Y is an abstraction. The real Lie algebra human cyclical threesome is an outcome of the representation in terms of numbers and matrices, the expression of duality in terms of -1, i, and position.
- Jacob Lurie, Bachelor's thesis, On Simply Laced Lie Algebras and Their Minuscule Representations
- Does the Lie algebra bracket express slack?
- Every root can be a simple root. The angle between them can be made {$60^{\circ}$} by switching sign. {$\Delta_i - \Delta_j$} is {$30^{\circ}$} {$\Delta_i - \Delta_j$}
- {$e^{\sum k_i \Delta_i}$}
- Has inner product iff {$AA^?=I$}, {$A{-1}=A^?$}
- Killing form. What is it for exceptional Lie groups?
- The Cartan matrix expresses the amount of slack in the world.
- {$A_n$} God. {$B_n$}, {$C_n$}, {$D_n$} human. {$E_n$} n=8,7,6,5,4,3 divisions of everything.
- 2 independent roots, independent dimensions, yield a "square root" (?)
- Symplectic matrix (quaternions) describe local pairs (Position, momentum). Real matrix describes global pairs: Odd and even?
- Root system is a navigation system. It shows that we can navigate the space in a logical manner in each direction. There can't be two points in the same direction. Therefore a cube is not acceptable. The determinant works to maintain the navigational system. If a cube is inherently impossible, then there can't be a trifold branching.
- {$A_n$} is based on differences {$x_i-x_j$}. They are a higher grid risen above the lower grid {$x_i$}. Whereas the others are aren't based on differences and collapse into the lower grid. How to understand this? How does it relate to duality and the way it is expressed.
- In {A_1}, the root {$x_2-x_1$} is normal to {$x_1+x_2$}. In {A_2}, the roots are normal to {$x_1+x_2+x_3$}.
- If two roots are separated by more than {$90^\circ$}, then adding them together yields a new root.
- {$cos\theta = \frac{a\circ b}{\left \| a \right \|\left \| b \right \|}$}
- {$120^\circ$} yields {$\frac{-1}{\sqrt{2}\sqrt{2}}=\frac{-1}{2}$}
- Given a chain of composition {$\cdots f_{i-1}\circ f_i \circ f_{i+1} \cdots$} there is a duality as regards reading it forwards or backwards, stepping in or climbing out. There is the possiblity of switching adjacent functions at each dot. So each dot corresponds to a node in the Dynkin diagram. And the duality is affected by what happens at an extreme.
- Root systems give the ways of composing perspectives-dimensions.
- {$A_n$} root system grows like 2,6,12,20, so the positive roots grow like 1,3,6,10 which is {$\frac{n(n+1)}{2}$}.
- A root pair {$x$} and {$-x$} yields directions such as "up" {$x––x$} and "down" {$–x–+x$}.
- Three-cycle: same + different => different ; different + different => same ; different + same => different
- {$ \begin{pmatrix}1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix}0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix}0 & -i \\ i & 0 \end{pmatrix} \begin{pmatrix}1 & 0 \\ 0 & -1 \end{pmatrix} $}
- same + different + different + same + ...
- Go from rather arbitrary set of dimensions to more natural set of dimensions. Natural because they are convenient. This leads to symmetry. Thus represent in terms of symmetry group, namely Lie groups. There are dimensions. In order to write them up, we want more efficient representations. Subgroups give us understanding of causes. Smaller representations give us understanding of effects. We want to study what we don't understand. In engineering, we leverage what we don't understand.
- Differences between even and odd for orthogonal matrices as to whether they can be paired (into complex variables) or not.
- {$e^{\sum i \times generator \times parameter}$} has an inverse.
- Unitary T = {$e^{iX_j\alpha_j}$} where {$X_j$} are generators and {$\alpha_j$} are angles. Volume preserving, thus preserving norms. Length is one.
- Complex models continuous motion. Symplectic - slack in continuous motion.
- Edward Frenkel. Langlands program, vertex algebras related to simple Lie groups, detailed analysis of SU(2) and U(1) gauge theories. https://arxiv.org/abs/1805.00203
- Consider the classification of Lie groups in terms of the objects for which they are symmetries.
- {$A^TA$} is similar to the adjoint functors - they may be inverses (in the case of a unitary matrix) or they may be similar.
- In the context {$e^iX$} the positive or negative sign of {$X$} becomes irrelevant. In that sense, we can say {$i^2=1$}. In other words, {$i$} and {$-1$} become conjugates. Similarly, {$XY-YX = \overline{-(YX-XY)}$}.
- What is the relation between the the chain of Weyl group reflections, paths in the root system, the Dynkin diagram chain, and the Lie group chain.
- One-dimensional proteins are wound up like the chain of a multidimensional Lie group.
- Išsakyti grupės {$G_2$} santykį su jos atvirkštine. Ar ši grupė tausoja kokią nors normą?
- The analysis in a Lie group is all expressed by the behavior of the epsilon.
- A_n defines a linear algebra and other root systems add additional structure
- A circle, as an abelian Lie group, is a "zero", which is a link in a Dynkin diagram, linking two simple roots, two dimensions.
- Video: The rotation group and all that
- Lorenzo Sadun. Videos: Linear Algebra Nr.88 is SO(3) and so(3)
- {$U(n)$} is a real form of {$GL(n,\mathbb{C})$}. Encyclopedia: Complexification of a Lie group
- DrPhysicsA. Particle Physics 4: Rotation Operators, SU(3)xSU(2)xU(1)
- At the level of forms, this can be seen by decomposing a Hermitian form into its real and imaginary parts: the real part is symmetric (orthogonal), and the imaginary part is skew-symmetric (symplectic)—and these are related by the complex structure (which is the compatibility).
- Particle physics is based on SU(3)xSU(2)xU(1). Can U(1) be understood as SU(1)xSU(0)? U(1) = SU(1) x R where R gives the length. So this suggests SU(0) = R. In what sense does that make sense?
- The conjugate i is evidently the part that adds a perspective. Then R is no perspective.
In what sense is SU(3) related to a rotation in octonion space?
- If SU(0) is R, then the real line is zero, and we have projective geometry for the simplexes. So the geometry is determined by the definition of M(0).
- {$SL(n)$} is not compact, which means that it goes off to infinity. It is like the totality. We have to restrict it, which yields {$A_n$}. Whereas the other Lie families are already restricted.
- The root systems are ways of linking perspectives. They may represent the operations. {$A_n$} is +0, and the others are +1, +2, +3. There can only be one operation at a time. And the exceptional root systems operate on these four operations.
- Real forms - Satake diagrams - are like being stepped into a perspective (from some perspective within a chain). An odd-dimensional real orthogonal case is stepped-in and even-dimensional is stepped out. Complex case combines the two, and quaternion case combines them yet again. For consciousness.
- Note that given a chain of perspectives, the possibilities for branching are highly limited, as they are with Dynkin diagrams.
- Solvable Lie algebras are like degenerate matrices, they are poorly behaved. If we eliminate them, then the remaining semisimple Lie algebras are beautifully behaved. In this sense, abelian Lie algebras are poorly behaved.
- Study how orthogonal and symplectic matrices are subsets of special linear matrices. In what sense are R and H subsets of C?
- Find the proof and understand it: "An important property of connected Lie groups is that every open set of the identity generates the entire Lie group. Thus all there is to know about a connected Lie group is encoded near the identity." (Ruben Arenas)
- Differentiating {$AA^{-1}=I$} at {$A(0)=I$} we get {$A(A^{-1})'+A'A^{-1}=0$} and so {$A'=-(A^{-1})'$} for any element {$A'$} of a Lie algebra.
- For any {$A$} and {$B$} in Lie algebra {$\mathfrak{g}$}, {$exp(A+B) = exp(A) + exp(B)$} if and only if {$[A,B]=0$}.
- Symmetry of axes - Bn, Cn - leads, in the case of symmetry, to the equivalence of the total symmetry with the individual symmetries, so that for Dn we must divide by two the hyperoctahedral group.
- the unitary matrix in the polar decomposition of an invertible matrix is uniquely defined.
- In {$D_n$}, think of {$x_i-x_j$} and {$x_i+x_j$} as complex conjugates.
- In Lie root systems, reflections yield a geometry. They also yield an algebra of what addition of root is allowable.
- Special linear group has determinant 1. In general when the determinant is +/- 1 then by Cramer's rule this means that the inverse is an integer and so can have a combinatorial interpretation as such. It means that we can have combinatorial symmetry between a matrix and its inverse - neither is distinguished.
- Determinant 1 iff trace is 0. And trace is 0 makes for the links +1 with -1. It grows by adding such rows.
- {$A_n$} tracefree condition is similar to working with independent variables in the the center of mass frame of a multiparticle system. (Sunil, Mukunda). In other words, the system has a center! And every subsystem has a center.
- Symplectic algebras are always even dimensional whereas orthogonal algebras can be odd or even. What do odd dimensional orthogonal algebras mean? How are we to understand them?
- An relates to "center of mass". How does this relate to the asymmetry of whole and center?
- Išėjimas už savęs reiškiasi kaip susilankstymas, išsivertimas, užtat tėra keturi skaičiai: +0, +1, +2, +3. Šie pirmieji skaičiai yra išskirtiniai. Toliau gaunasi (didėjančio ir mažėjančio laisvumo palaikomas) bendras skaičiavimas, yra dešimts tūkstantys daiktų, kaip sako Dao De Jing. Trečias yra begalybė.
- Kaip sekos lankstymą susieti su baltymų lankstymu ir pasukimu?
- Fizikoje, posūkis yra viskas. Palyginti su ortogonaline grupe.
- {$x_0$} is fundamentally different from {$x_i$}. The former appears in the positive form {$\pm(x_0-x_1)$} but the others appear both positive and negative.
- Kaip dvi skaičiavimo kryptis (conjugate) sujungti apsisukimu?
- How to interpret possible expansions? For example, composition of function has a distinctive direction. Whereas a commutative product, or a set, does not.
- Dots in Dynkin diagrams are figures in the geometry, and edges are invariant relationships. A point can lie on a line, a line can lie on a plane. Those relationships are invariant under the actions of the symmetries. Dots in a Dynkin diagram correspond to maximal parabolic subgroups. They are the stablizer groups of these types of figures.
- G2 requires three lines to get between any two points (?) Relate this to the three-cycle.
Inner product
- Hermitian: a+bi <-> a-bi, Symmetric: a <-> a, Anti-symmetric: b <-> -b
- Consider how the "inner product", including for the symplectic form, yields geometry.
- The skew-symmetric bilinear form says that phi(x,y)= -phi(y,x) so one of them, say, (x,y) is + (correct) and the other is - (incorrect). This is left-right duality based on nonequality (the two must be different). And it is threefold logic, the non-excluded middle 0. SO that 1 true, -1 false, 0 middle.
- The inner products (like unitary) are linear. They and their quadratic product get projected onto a second quadratic space (a screen) which expresses their geometric nature as a tangent space for a differentiable manifold thus relating the discrete and the continuum, the infinitesimal and the global (like Mobius transformations).
- Three inner products - relate to chronogeometry.
- Three inner products are products of vectors that are external sums of basis vectors as different units. Six interpretations of scalar multiplication that are internal sums of amounts.
Coxeter groups
- Understand the classification of Coxeter groups.
- Organize for myself the Coxeter groups based on how they are built from reflections.
Exponentiation
- Integral of 1/x is ln x what does that say about ex?
- {$2\pi$} additive factors, e multiplicative factors.
- Math Companion section on Exponentiation. The natural way to think of {$e^x$} is the limit of {$(1 + \frac{x}{n})^n$}. When x is complex, {$\pi i$}, then multiplication of y has the effect of a linear combination of n tiny rotations of {$\frac{\pi}{n}$}, so it is linear around a circle, bringing us to -1 or all the way around to 1. When x is real, then multiplication of y has the effect of nonlinearly resizing it by the limit, and the resulting e is halfway to infinity.
Rotation
- Usually multiplication by i is identified with a rotation of 90 degrees. However, we can instead identify it with a rotation of 180 degrees if we consider, as in the case of spinors, that the first time around it adds a sign of -1, and it needs to go around twice in order to establish a sign of +1. This is the definition that makes spin composition work in three dimensions, for the quaternions. The usual geometric interpretation of complex numbers is then a particular reinterpretation that is possible but not canonical. Rotation gets you on the other side of the page.
- If we think of rotation by i as relating two dimensions, then {$i^2$} takes a dimension to its negative. So that is helpful when we are thinking of the "extra" distinguished dimensions (1). And if that dimension is attributed to a line, then this interpretation reflects along that line. But when we compare rotations as such, then we are not comparing lines, but rather rotations. In this case if we perform an entire rotation, then we flip the rotations for that other dimension that we have rotated about. So this means that the relation between rotations as such is very different than the relation with the isolated distinguised dimension. The relations between rotations is such is, I think, given by {$A_n$} whereas the distinguished dimension is an extra dimension which gets represented, I think, in terms of {$B_n$}, as the short root.
- This is the difference between thinking of the negative dimension as "explicitly" written out, or thinking of it as simply as one of two "implicit" states that we switch between.
- Rotation relates one dimension to two others. How does this rotation work in higher dimensions? To what extent does multiplication of rotation (through three dimensional half turns) work in higher dimensions and how does it break down?
- Lie groups are ambiguous in that they have an algebraic structure and also an analytic structure, thus yielding a geometric structure.
- Takagi decomposition - prove combinatorially - unitary matrices.
- https://en.wikipedia.org/wiki/Matrix_decomposition
- In Lie theory, how is the adjoint functor related to adjunction?
- The multiplicative group of the unit quaternions are isomorphic to SU(2). In what sense are they three-dimensional?
Lie theory
- Lie algebra is an algebra of dimensions.
 Root system The root system of {$E_8$} can be thought of as a full system. The root system of {$E_7$} is then the set of vectors that are perpendicular to one root. {$E_6$} is the set of vectors that are perpendicular to two suitably choosen roots. What would be the root system gotten that is perpendicular to three suitably choosen roots from {$E_8$}? or more roots? {$D_6$} is the set of vectors that is perpendicular to one root in {$E_7$}.
Root system The root system of {$E_8$} can be thought of as a full system. The root system of {$E_7$} is then the set of vectors that are perpendicular to one root. {$E_6$} is the set of vectors that are perpendicular to two suitably choosen roots. What would be the root system gotten that is perpendicular to three suitably choosen roots from {$E_8$}? or more roots? {$D_6$} is the set of vectors that is perpendicular to one root in {$E_7$}.
- Think about the Lie algebra root systems in terms of how the roots expand upon {$\pm(x_i-x_j)$} for {$A_n$}. We have:
| {$B_n:\pm (x_i+x_j), \pm x_i$} | {$C_n:\pm (x_i+x_j), \pm 2x_i$} | {$D_n:\pm (x_i+x_j), i\neq j$} |
- https://www.math.miami.edu/~armstrong/Talks/What_is_ADE.pdf
- Wildberger. Consider how the mutation games express how and why the four classical Lie groups get distinguished. How is this expressed in the Lie groups and in geometry? How does this relate to the propagation of signal that I had observed? And what is going on with the exceptional Lie algebras?
- Representation theory of Lie algebras and groups
- Lie groups and algebras express (continuous) symmetry that I am discovering at various meta levels.
- Spin gives the number of choices. Boson - odd number (includes zero), fermion even number (does not include zero). How does that relate to the kinds of classical Lie algebras?
- {$F_1$} photon chooses from one choice
- {$F_2$} electron chooses from two choices
- {$F_3$} spin one boson chooses from three choices
- {$F_5$} spin two graviton chooses from five choices (fivesome for space and time?)
Do these relate to the divisions of everything? What happens with the eightsome? and ninesome?
- https://math.stackexchange.com/questions/1163032/geometric-intuitive-meaning-of-sl2-r-su2-etc-representation-the
- (B,N) pair for finite simple groups.
- Vidas Regelskis - quantum group theory and applications to mathematical physics.
- The permutation representation is just one dimension different than the (geometrical) standard representation. The former is the basis for the root system {$x_i$} and the latter is the basis for the root system {$x_i-x_{i+1}$}. How do the classical Lie families relate them? Is that related to Jucys elements?
- Regarding root systems: Two rotations of 135 degrees in the plane give perpendicularity. But two rotations of 120 degrees can also give perpendicularity if we leave the plane and come back to it.
Lie theory: Geometry takes place on spheres
- Odd dimensional real sphere
- Even dimensional real sphere
- Complex sphere
- Quaternionic sphere
Lie algebra - learning cycle - describes the learning structure for a Lie group. Compare with a point (an answer) and with an investigation (variation, perturbation, loops).
Lie families
| {$A_m$} | SU(m+1) | dual | conformal |
| {$B_m$} | SO(2m+1) | external zero | sphere has two extremes - Riemann sphere - projective |
| {$D_m$} | SO(2m) | fuse internal zero | rotate circle - affine |
| {$C_m$} | Sp(2m) | fold | symplectic |
Lie theory
- How does the adjoint representation (for a Lie group) relate to adjoint functors?
- SO(3,1) is isomorphic (as algebras, with complexification, not as groups) to SU(2) tensor SU(2)
Affine root system, affine Lie algebra and affine geometry are related by affine connection.
- In a Dynkin diagram chain, the full length gives the totality - the pseudovector - and is relevant for the duality of counting forwards and backwards. And for that duality we need to reverse everything, reorganize everything, reorder all of the simple roots, and so each root is a relevant cycle for permuting and contributes to the sign {$(-1)^{\frac{n(n+1)}{2}}$} or thereabouts.
- Think of Dynkin diagrams as related to Zeng trees and imagine how the diagrams express the double root or single root.
- https://en.m.wikipedia.org/wiki/Whitehead_product
- https://en.m.wikipedia.org/wiki/Quasi-Lie_algebra
- https://en.m.wikipedia.org/wiki/Generalised_Whitehead_product
Duality of counting
- Increasing slack takes us from O to n with n growing as it counts towards infinity. Decreasing slack has us count backwards down from n to 0.
Mano diagramos
- https://www.math3d.org/m8XN5esA2 diagram of A3 root system and cube
- https://www.math3d.org/w3h4VbZg7 diagram of A3 root system
Dynkin diagrams
- How do the exceptional Dynkin diagrams (and root systems) model counting? It must be particular and restrictive. For the E-sequence, think of the math problem with two white knights and two black knights, asking how they might exchange places. The problem has to be redrawn as a state diagram and it turns out that it is a line but with one ability to side step the line just as with the E-sequence. So the counting could involve a side-stepping in memory.
- {$\mathfrak{so}(n)=\{X\in\mathbb{R}[n]|X^{\dagger}=-X\}$}
- {$\mathfrak{su}(n)=\{X\in\mathbb{C}[n]|X^{\dagger}=-X\}$}
- {$\mathfrak{sp}(n)=\{X\in\mathbb{H}[n]|X^{\dagger}=-X\}$}
Lie theory
- What is the relationship between matroids and root lattices? The Geometry of Root Systems and Signed Graphs
- Interesting example of nonlocality. Dynkin diagram chains can only have a widget at one end. The other end immediately knows that the other end has a widget.
Why can we comb even-dimensional spheres but not odd-dimensional spheres
Think about Dynkin diagrams and related lattices.
- BC_n lattice simple roots are: Face - Edge - Edge - Edge - Edge ...
- C_n looks like an octahedron. What does each lattice look like?
- Consider the cases of A_n and D_n how to picture that
- Consider the Weyl groups and what they are symmetries of.
Classify compact Lie groups because those are the ones that are folded up and then consider what it means to unfold them and that gives the lattice structure. So the root lattice shows how to unfold a compact Lie group into its universal covering. And this relates to the difference between the classical Lie groups as regards the duality between counting forwards and backwards. The counting takes place on the lattice. And you can fold or not in each dimension if you are working with the reals and so that gives you the real forms. But you can't fold along separate dimensions if you have the complexes so you have to fold them all.
- In what way is the folding-unfolding nonabelian or abelian?
- What does the folding-unfolding look like for exceptional Lie groups?
- How is the widget at the end of a Dynkin diagram serve as the origin (or outer edge?) for the unfolding?
- Consider how the histories in combinatorics unfold the objects. What are the possible structures for the histories? How do they relate to root systems? How do root lattices or other such structures express the possible ways that combinatorial objects can encode information by way of their histories?
- How is a perspective related to a one-dimensional line - lattice - circle ?
- Given the Lie group's torus T, Lie(T) / L = T, where L is a root lattice.
- Abelian Lie groups are toruses. So we are interested in maximal torus for the semi-simple Lie groups.
- Lie group G has the same Lie algebra as the identity component (as in the case when G is disconnected). And G has the same Lie algebra as any covering space of G.
- Lie bracket expresses the failure to commute. So that failure is part of the learning process.
- How are root lattices related to matroids?
Interpret {$x_i-x_j$} in {$A_n$} as a boundary map as in homology.
"Dynkin diagram: Geometry for an n-dimensional chain"
Independence is given by x_i. Interdependence is in the differences x_i - x_j.
Derive the Jacobi identity from the notion of an ideal of a Lie algebra as corresponding to a normal subgroup of a lie group
Show the noncommutativity of A_2
SL(2,C) character variety related to hyperbolic geometry. SL2(C) character varieties
Universal enveloping algebra is an abstraction where the generators are free and thus yield infinite generators. Whereas the Lie algebra may be in terms of concrete matrices and the underlying generators, when understood not in terms of the Lie bracket but in terms of matrix multiplication, may have relations such as {$x^2=0$}, {$h^2=1$}.
To what extent can the Lie correspondence be based not on infinitesimals but on the combinatorics of matrix exponentials?
Analyze rotations in toruses (in Lie groups) and match them (through exponential) with corresponding matrices in Lie algebras. For example, real 2x2 rotation matrix in terms of sines and cosines equals {e^M} where M has zeros on the diagonal and + and - theta on the off diagonal.
Compare the distinction of odd and even orthogonal groups with the group extension of {$\mathbb{Z}_2$}.
Spinors are how you turn around at the widget of the real orthogonal Dynkin diagrams.
Lie algebra is not associative but rather acts like the production for a Turing machine. A consequence of the Jacobi identity and anticommutativity:
- {$[x,[y,z]]-[[x,y],z]=[[z,x],y]$}
- {$a(bc)-(ab)c=(ca)b$}
Sobczyk. Vector Analysis of Spinors revised
Examine the root systems for the exceptional Lie algebras. In what sense are they expressing the duality in counting forwards and backwards?
Since the classical Lie families present the symmetry in counting forwards and backwards, could the exception Lie groups and algebras present the symmetry in counting on an eight-cycle, using and not using a certain number of tracks?
Lie groups and algebras capture the symmetries in math by capturing how basic structures can operate in both algebra and analysis simultaneously. Algebra expresses what is, and analysis (as with homology) expresses what is not (as with holes).
In Lie group for rotations, SO(3), the bracket of [x,y] gives you z.
Coxeter diagram {$D_n$} symmetry group of demicube: every other vertex of a hypercube. Is that related to a coordinate space? Combinatorially, can we flip the vectors of the demicube to get a coordinate system?
{$G_2$} has two simple roots: {$\alpha=e_1-e_2$} and {$\beta=(e_2-e_1)+(e_2-e_3)$}. The combinations are {$\pm\alpha$} and {$\pm(\beta + n \alpha)$} where {$n=0,1,2,3$} and {$\pm(2\beta + 3\alpha)$}
Relate the long root (2 to 1) in the simple root diagram of {$G_2$} with John Baez's spans of groupoids.
Math Stack Exchange. Prove that the manifold SO(n) is connected.
Cube reflections given by vectors u, v, w from the center of the cube to the center of a face, the center of an edge, and the center of another edge. And the angles between the vectors are pi/2, pi/3 and pi/4. And the two edge midpoints are separated by pi/3 so rotating through six such edges gets you back. And that is the chain for the Dynkin diagram.
