- MathNotebook
- MathConcepts
- StudyMath
- Geometry
- Logic
- Bott periodicity
- CategoryTheory
- FieldWithOneElement
- MathDiscovery
- Math Connections
Epistemology
- m a t h 4 w i s d o m - g m a i l
- +370 607 27 665
- My work is in the Public Domain for all to share freely.
- 读物 书 影片 维基百科
Introduction E9F5FC
Questions FFFFC0
Software
Bott periodicity, Bott periodicity flavors, Bott periodicity models divisions, Clifford algebras, Topological invariants, Symmetric spaces, Linear complex structure, Octonions, Lie theory, Compact Lie Group Dimensions, Embedding UXU
Understand Lie Group embeddings and how linear complex structures code the three minds and eight divisions of everything.
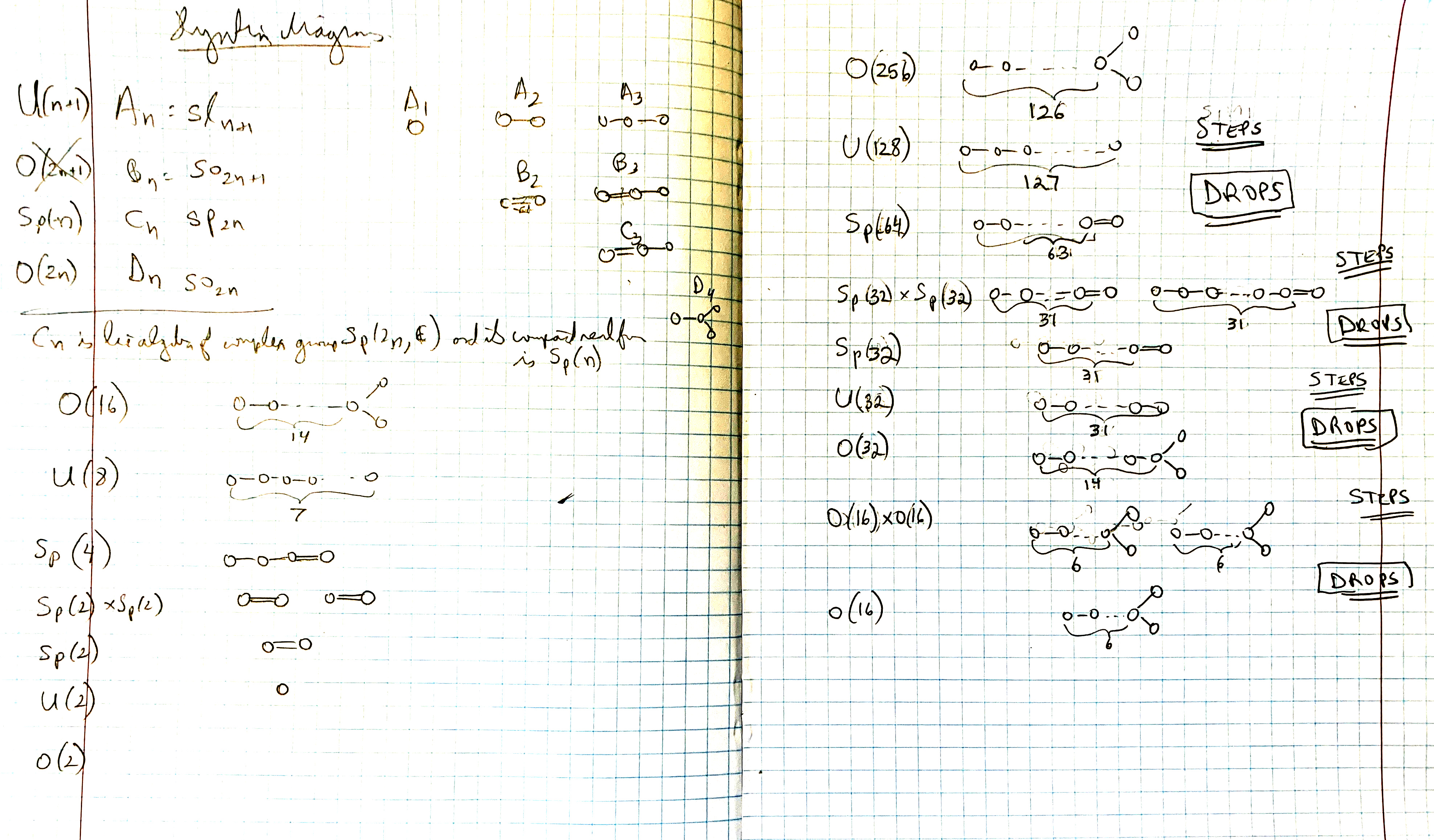
Lie Group Embeddings
- Understand the dimensions of the Lie groups in terms of their root systems.
- How do the root systems fit together as we go through the embeddings?
- Is there a way to describe orthogonal matrices in {$O(16)$} where we could show how more and more structure gets added as we proceed through the embeddings?
- What is the significance of a subspace commuting with an operator?
- How is the orthogonal group O(2) related to spinors?
- Are orthogonal, unitary, symplectic matrices expressible so that they, respectively, consists of real, complex or quaternionic rotations?
- How are the (nonassociative) octonions related to the (associative) split-biquaternions?
- What is the relationship between {$J_1J_2J_3J_4$} of 8-fold Bott periodicity and {$i$} of 2-fold Bott periodicity? Consider how they relate to the homotopy group {$\mathbb{Z}$} and the splitting of the Lie group.
- Show that {$U(8)$} contains {$O(4)\times O(4)$}.
- Why does {$O(16)$} lead to {$U(8)$} rather than {$O(8)\times O(8)$}?
- Why does {$O(2)$} lead to {$O(1)\times O(1)$} rather than {$U(1)$}?
- Why does {$Sp(4)$} lead to {$Sp(2)\times Sp(2)$} rather than {$U(4)$}?
- Why does {$Sp(2)$} lead to {$U(2)$} rather than {$Sp(1)\times Sp(1)$}?
- How do two fourfold structures {$J_1,J_2,J_3,J_4$} and {$J_5,J_6,J_7,J_8$} fit together?
- Understand the homotopy groups {$\mathbb{Z}_2$} and {$0$} with regard to reflection.
{$O(16r)\supset U(8r)\supset Sp(4r)\supset Sp(2r)\times Sp(2r) \supset Sp(2r) \supset U(2r) \supset O(2r) \supset O(r)\times O(r) \supset O(r)$}
Note that we can start anywhere. We simply forget the previous complex structures. Thus the division of everything incorporates a new perspective, yielding a new division of everything, by way of the operation +1, or similarly, +2 or +3.
{$O(16)\Rightarrow U(8)$}
Write the linear complex structure {$J_1$} as:
{$J_1=\begin{pmatrix} 0 & -1 & & & \\ 1 & 0 & & & \\ & & 0 & -1 & \\ & & 1 & 0 & \\ & & & & \ddots \end{pmatrix}$}
What orthogonal matrices {$O$} commute with {$J_1$} so that {$OJ_1=J_1O\;$}?
Multiplying out we see that we get {$2\times 2$} blocks which express complex numbers.
{$\begin{pmatrix} a & -b \\ b & a \end{pmatrix}$}
Rotations commute and rotoreflections do not.
When we have four linear complex structures {$J_\alpha, J_\beta, J_\gamma, J_\delta$}, any two of them yield a shift in perspective (a quaternionic structure), and any three of them ground three-cycles on a splitting of the vector space. Putting that together we may have possibly
{$U(8)\Rightarrow Sp(4)$}
What unitary matrices {$U$} commute with {$J_1$} so that {$UJ_1=J_1U\;$}?
{$\begin{pmatrix} x & y \\ -\bar{y} & \bar{x} \end{pmatrix}$}
{$Sp(4)\Rightarrow Sp(2)\times Sp(2)$}
{$\begin{pmatrix} Sp(2) & 0 \\ 0 & Sp(2) \end{pmatrix}$}
{$Sp(2)\times Sp(2)\Rightarrow Sp(2)$}
{$\begin{pmatrix} Sp(2) & 0 \\ 0 & \textrm{same} \end{pmatrix}$} with blocks {$\begin{pmatrix} x & y \\ -\bar{y} & \bar{x} \end{pmatrix}$}
{$Sp(2)\Rightarrow U(2)$}
{$\begin{pmatrix} U(2) & 0 \\ 0 & \textrm{same} \end{pmatrix}$} with blocks {$\begin{pmatrix} x & 0 \\ 0 & \bar{x} \end{pmatrix}$}
{$U(2)\Rightarrow O(2)$}
{$\begin{pmatrix} O(2) & 0 \\ 0 & \textrm{same} \end{pmatrix}$} with blocks {$\begin{pmatrix} a & 0 & 0 & 0 \\ 0 & a & 0 & 0 \\ 0 & 0 & a & 0 \\ 0 & 0 & 0 & a \end{pmatrix}$}
{$O(2)\Rightarrow O(1)\times O(1)$}
{$\begin{pmatrix} O(1) & 0 & 0 \\ 0 & O(1) & 0 \\ 0 & 0 & \textrm{same} \end{pmatrix}$} with blocks {$\begin{pmatrix} a & 0 & 0 & 0 \\ 0 & a & 0 & 0 \\ 0 & 0 & a & 0 \\ 0 & 0 & 0 & a \end{pmatrix}$}
Note that {$O(1)=\{(1),(-1)\}$} so {$a=1$} or {$a=-1$}. But also, we could have started with {$O(16r)$} and we could have here {$O(r)$}.
{$O(1)\times O(1)\Rightarrow O(1)$}
{$\begin{pmatrix} O(1) & 0 & 0 \\ 0 & \textrm{same}\; O(1) & 0 \\ 0 & 0 & \textrm{same}\;O(1)\times O(1) \end{pmatrix}$} with blocks {$\begin{pmatrix} a & 0 & 0 & 0 \\ 0 & a & 0 & 0 \\ 0 & 0 & a & 0 \\ 0 & 0 & 0 & a \end{pmatrix}$}
Unitary Group Embeddings
{$U(2r) \supset U(r)\times U(r) \supset U(r)$}
We define transformations {$K_1=iJ_1$} and {$K_2=iJ_2$}. {$K_k^2=I$}, {$(K_k+1)(K_k-1)=0$}, {$(K_k+1)(K_k-1)v=0$}, so {$K_kv=v$} or {$K_kv=-v$}. {$K_k$} thus splits {$\mathbb{C}^{2r}$} into two eigenspaces.
Note that {$J_kv=-iv$} or {$J_kv=iv$}. In other words, the eigenvalues of {$J_k$} are {$\pm i$}.
{$U(2)\Rightarrow U(1)\times U(1)$}
Consider the effect of {$J_1$} on {$J_1v$}. We have {$J_1^2=-1$} thus {$J_1(J_1v)=-v$}.
Suppose {$v$} is such that {$J_1v=-iv$}. Then {$J_1(J_1v)=-iJ_1v$} and thus {$J_1v$} is in the same eigenspace as {$v$}.
Likewise, suppose {$v$} is such that {$J_1v=iv$}. Then {$J_1(J_1v)=iJ_1v$} and thus {$J_1v$} is in the same eigenspace as {$v$}.
Thus {$J_1$} does not take us from one eigenspace to another. This is because {$i$} is a scalar.
Suppose a unitary matrix {$U$} commutes with {$J_1$}, which is to say, {$UJ_1=J_1U$}.
Suppose {$v$} is such that {$J_1v=iv$}. What can we say about {$Uv$}? {$J_1Uv=UJ_1v=Uiv=iUv$}.
Similarly, suppose {$v$} is such that {$J_1v=-iv$}. Then {$J_1Uv=UJ_1v=U(-iv)=-iUv$}.
Thus {$U$} respects the eigenspaces. If the eigenspaces are the same size, then {$U\in U(1)\times U(1)$}.
Can we say, conversely, that {$U(1)\times U(1)$} consists of all of the unitary matrices that commute with {$J_1$}?
{$U(1)\times U(1)\Rightarrow U(1)$}
Dynkin Diagrams
Fibre Bundles
Shintaro Fushida-Hardy. Notes for MATH 282B Homotopy Theory. Explains fibrations and basic examples of fibre bundles involving Lie groups and also projective spaces. Also talks about loop spaces.
{$$\mathbb{S}^0\hookrightarrow \mathbb{S}^n\hookrightarrow \mathbb{R}\mathbb{P}^n$$} {$$\mathbb{S}^1\hookrightarrow \mathbb{S}^{2n+1}\hookrightarrow \mathbb{C}\mathbb{P}^n$$} {$$\mathbb{S}^3\hookrightarrow \mathbb{S}^{4n+3}\hookrightarrow \mathbb{H}\mathbb{P}^n$$}
{$$\mathbb{C}\mathbb{P}^1\cong\mathbb{S}^2=\mathbb{C}\cup\{\infty\}$$}
{$$\mathbb{S}^1\hookrightarrow \mathbb{S}^{3}\hookrightarrow \mathbb{S}^{2}$$}
{$$0=\pi_3(\mathbb{S}^1)\to\pi_3(\mathbb{S}^3)\to\pi_3(\mathbb{S}^2)\to\pi_2(\mathbb{S}^1)=0$$}
thus {$\pi_3(\mathbb{S}^2)\cong\pi_3(\mathbb{S}^3)=\mathbb{Z}$}
{$$\mathbb{S}^3\hookrightarrow \mathbb{S}^{7}\hookrightarrow \mathbb{S}^{4}$$}
{$$O(n-1)\hookrightarrow O(n)\hookrightarrow \mathbb{S}^{n-1}$$}
{$$U(n-1)\hookrightarrow U(n)\hookrightarrow \mathbb{S}^{2n+1}$$}
{$$Sp(n-1)\hookrightarrow Sp(n)\hookrightarrow \mathbb{S}^{4n+1}$$}
thus {$\pi_k(O(n-1))\cong\pi_k(O(n))$} for {$k<n-2$}.
Grassmannian {$G(n,k)=G_n(\mathbb{R}^k)$} is the {$n$}-planes in {$\mathbb{R}^k$}
{$V(n,k)=V_n(\mathbb{R}^k)$} are the orthonormal sets of size {$n$} in {$\mathbb{R}^k$}
Suppose {$n < m < k$}.
{$$O(n)\hookrightarrow V(n,k)\hookrightarrow G(n,k)$$}
{$$OV(m − n,k − n)\to V (m, k) \to V (n, k)$$}
{$$V(m − 1, k − 1) \to V(m, k) \to S^{k−1}$$} when {$n=1$}
Thus {$V(m, k)$} is {$(k − m − 1)$}-connected. Consequently, {$V(m, \infty)$} is weakly contractible.
From our sequence {$O(n)\hookrightarrow V(n,k)\hookrightarrow G(n,k)$} we have that {$\pi_n(G(m,\infty))\cong\pi_{n-1}(O(m))$}, yielding {$G(m,\infty)\cong BO(m)$}.
More Facts and Thoughts
Note that for {$O(2n)\supset O(n)\times O(n)$} we have not just that {$O(n)\times O(n)$} are the matrices that commute with {$J_7$}, but also that there exist mutually anticommuting {$J_1,J_2,J_3,J_4,J_5,J_6$} which anticommute with {$J_7$} and commute with {$O(2n)$}. This means that {$O(2n)\supset U(n)\nsupseteq O(n)\times O(n)$} for the other linear complex structures constrain {$J_7$} so that it does not commute with all of {$U(n)$} but only part of it.
Analyzing the dimensions
- {$O(n)$} has {$n(n-1)/2$} real dimensions
- {$U(n)$} has {$n^2$} real dimensions
- {$Sp(n)$} has {$n(2n+1)$} real dimensions
- {$O(16)$} has {$120$} real dimensions; {$U(8)$} has {$64$}; {$Sp(4)$} has {$36$}; {$Sp(2)\times Sp(2)$} has {$20$}; {$Sp(2)$} has {$10$}; {$U(2)$} has {$4$}; {$O(2)$} has {$3$};{$O(1)\times O(1)$} has {$0$}; {$O(1)$} has {$0$}.
- {$O(4)\times O(4)$} has {$12$} real dimensions.
Karoubi: The classical groups are built from spheres as fibrations: {$O(n)\rightarrow O(n+1)\rightarrow S^{n}$} and {$U(n)\rightarrow U(n+1)\rightarrow S^{2n+1}$}. From these fibrations it immediately follows that the homotopy groups of {$O(n)$} and {$U(n)$} stabilize.
{$\pi_i(O(n))\cong\pi_i(O(n+1))$} for {$n>i/2$} and {$\pi_i(U(n))\cong\pi_i(U(n+1))$} for {$n>i+1$}
Using polar decomposition of matrices, in the Bott periodicity theorem, we can replace {$O(n)$} and {$U(n)$} and {$Sp(n)$} with {$GL(\mathbb{R})$} and {$GL(\mathbb{C})$} and {$GL(\mathbb{H})$}, respectively.