Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

Note! For my discussion of the binomial theorem, please see here.

Underyling coordinates

{$\{x_1, x_2, \cdots \}$}

Root system

Root systems

• {$A_1 = \{x_2-x_1, x_1-x_2\}$}

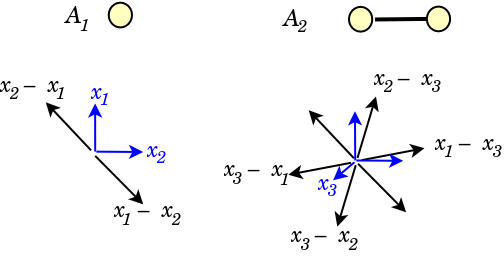
Note that {$\{x_1-x_2,x_1,x_1+x_2,x_2\}$} form a harmonic range.

From root system to complex Lie algebra

The Chevalley–Serre relations yield a Lie algebra from a root system. The simple roots {$\Delta$} and their Cartan matrix give rise to generators {$H_\lambda$}, {$X_\lambda$}, {$Y_\lambda$}. In general, for each pair of roots we have an "externally expressed" pair {$X_r$} and {$Y_r$} and also an "internally expressed" pair {$H_r$}. The externally expressed pair yields the internally expressed pair: {$[X_r,Y_r]=H_r$}. The Cartan matrix relates the internally expressed pair and the externally expressed pair: {$[H_r,X_s]=C_{r,s}X_s$} and {$[H_r,Y_s]=-C_{r,s}Y_s$}.

In the case when {$\Delta$} is simply {$r=x_2-x_1$}, the Cartan matrix is {$C=\begin{pmatrix} 2 \end{pmatrix}$}

and we have:

{$[H_r,X_r]=C_{r,r}X_r=2X_r$}

{$[H_r,Y_r]=C_{r,r}Y_r=-2Y_r$}

{$[X_r,Y_r]=H_r$}

Note that {$[X_r,Y_r]$} is an external conjugate, whereas {$H_r=\begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}$} is an internal conjugate.

{$H_i$} and {$H_{i+1}$} are separated by {$120^{\circ}$}.

Matrices act on a vector space

{$H_i$} acts on vectors {$e_i=(0,\cdots,0,1,0,\cdots,0)$}. With the ordinary matrix action we have {$H_ie_i=e_i$}. With the Lie algebra action we have {$[H_i,e_i]=e_i--e_i=2e_i$}.

Basis for complex Lie algebra

{$H=\begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix} X=\begin{pmatrix} 0 & 1\\ 0 & 0 \end{pmatrix} Y=\begin{pmatrix} 0 & 0\\ 1 & 0 \end{pmatrix}$}

{$[H,X]=2X, [H,Y]=-2Y, [X,Y]=H$}

Complex semisimple Lie algebra {$\frak{g}$} has Cartan subalgebra {$\frak{h}$}.

The elements in the Lie algebra have the form:

{$c_{11}H + c_{12}X + c_{21}Y$}

Where {$c_{11},c_{12},c_{21}\in\mathbb{C}$}. In other words:

{$M=\begin{pmatrix} c_{11} & c_{12}\\ c_{21} & -c_{11} \end{pmatrix}$}

The basis is given by setting one variable to {$1$} and the rest to {$0$}:

• {$c_{11}=1,c_{12}=0,c_{21}=0$}
• {$c_{11}=0,c_{12}=1,c_{21}=0$}
• {$c_{11}=0,c_{12}=0,c_{21}=1$}

{${H}$} is a basis for {$\frak{h}$}.

{$\alpha \in \frak{h}^*$} is a root of {$\frak{g}$} relative to {$\frak{h}$} if {$\alpha \neq 0$} and there exists some {$X \neq 0 \in \frak{g}$} such that

{$[H,X]=\alpha(H)X$} for all {$H\in\frak{h}$}.

{$$ \matrix{ \text{Lie}(G_{\mathbb{C}}) & \underset{\text{exponential}}{\rightarrow} & G_{\mathbb{C}} \cr \uparrow{\scriptsize\text{complexify real form}} & & \uparrow \scriptsize\text{complexify group} \cr \text{Lie}(G_{\mathbb{R}}) & \underset{\text{exponential}}{\rightarrow} & G_{\mathbb{R}} \cr } $$}

For example:

{$$ \matrix{ \frak{sl}(2,\mathbb{C}) & \underset{\text{exponential}}{\rightarrow} & \text{SL}(2,\mathbb{C}) \cr \uparrow{\scriptsize\text{complexify real form}} & & \uparrow \scriptsize\text{complexify group} \cr \frak{su}(2) & \underset{\text{exponential}}{\rightarrow} & \text{SU}(2) \cr } $$}

Complexification of a real Lie algebra

A real Lie subalgebra {$\frak{f}$} of a complex Lie algebra {$\frak{h}$} is called a real form of {$\frak{h}$} if each element {$x\in \frak{h}$} is uniquely representable in the form {$x=u+iv$}, where {$u,v\in \frak{f}$}. The complexification of {$\frak{f}$} is naturally isomorphic to {$\frak{h}$}. See...

Basis for real Lie algebra

Pauli matrices {$\{\sigma_j\}$} are Hermitian ({$\sigma_j=\sigma_j^*$}) and unitary ({$\sigma_j^{-1}=\sigma_j^*$}):

{$\sigma_1=\begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix}\; \sigma_2=\begin{pmatrix} 0 & -i\\ i & 0 \end{pmatrix}\; \sigma_3=\begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}$}

{$\sigma_1=(X+Y)\; \sigma_2=i(X-Y)\; \sigma_3 = H$}

The algebra generated by these {$\{\sigma_j\}$} is isomorphic to the Clifford algebra of {$\mathbb{R}^3$}.

{$\sigma_1\sigma_2=i\sigma_3, \sigma_2\sigma_3=i\sigma_1, \sigma_3\sigma_1=i\sigma_2$}

The four symbols {$i,\sigma_1,\sigma_2,\sigma_3$} are four manifestations of {$i$}. In each case we can define the conjugate {$\bar{i}=-i$}. In each case, we can also define {$1$}. (Work out the subtleties in the different ways of denoting {$a\pm ib$}.)

In particular, the scalar {$i$} is a marker that indicates that composition proceeded in the marked direction, {$\sigma_1\sigma_2$} or {$\sigma_2\sigma_3$} or {$\sigma_3\sigma_1$}. Thus the equations above each conserve the power of {$i$}, which is {$2$} in each case, for a total value of {$i^2=-1$}, as in {$ii=ii$}.

{$\sigma_2\sigma_1=-i\sigma_3, \sigma_3\sigma_2=-i\sigma_1, \sigma_1\sigma_3=-i\sigma_2$}

In these equations, composition proceeds in the opposite direction, marked by the conjugate {$\bar{i}=-i$}. This yields {$\bar{i}\bar{i}$} and reversing the orientation of the symbol is multiplying by {$-1$}. Thus each symbol is oriented to be understood as reading from left to right or right to left.

The algebra generated by {$\{i\sigma_1,i\sigma_2,i\sigma_3\}$} is isomorphic to the quaternions.

The matrices {$\{i\sigma_1,i\sigma_2,i\sigma_3\}$} form a basis for the real Lie algebra {$\frak{su}(2)$}.

Study and verify this three-cycle. Note the importance of {$i$} in each element of {$\frak{su}(2)$}.

Note that these are the skew-adjoint matrices with trace 0. These are the matrices {$M$} for which {$b_{11}$},{$a_{12}$} and {$b_{12}$} are real.

{$M=i\begin{pmatrix} b_{11} & b_{12}+ia_{12}\\ b_{12}-ia_{12} & -b_{11} \end{pmatrix}$}

The basis is given by setting one variable to {$1$} and the rest to {$0$}:

• {$b_{11}=1,a_{12}=0,b_{12}=0$}
• {$b_{11}=0,a_{12}=1,b_{12}=0$}
• {$b_{11}=0,a_{12}=0,b_{12}=1$}

They are linear independent over {$\mathbb{R}$}. However, over {$\mathbb{C}$} we have:

• {$H=-i(u_3)$}
• {$X=-i(u_1+iu_2)/2$}
• {$Y=-i(u_1-iu_2)/2$}

which are not skew-adjoint.

Thus a pair X and Y of opposite roots in the complexification of the Lie algebra are "regrounding" their sum {$X+Y$} and difference (marked by {$i$}) {$i(X-Y)$} in the real Lie algebra. Restriction to linear relations with real number coefficients keeps {$X+Y$} and {$i(X-Y)$} different. Introducing linear relations with complex number coefficients allows them to be reexpressed in terms of {$X$} and {$Y$}.

Note that in the compact group these generators satisfy a three-cycle of relations: {$[u_3,u_1]=2u_2$}, {$[u_1,u_2]=2u_3$}, {$[u_2,u_3]=2u_1$}. [Sum, Difference]=2*Inner, [Difference,Inner]=2*Sum, [Inner,Sum]=2*Difference. The factor {$2$} comes from the commutator recording that the three-cycle holds in both directions, forwards (positive) {$u_1u_2=u_3$} and backwards (negative) {$u_2u_1=-u_3$} so that {$[u_1,u_2]=u_3--u_3=2u_3$}. If we divide each generator by {$2$}, then we will lose that factor: {$[\frac{u_3}{2},\frac{u_1}{2}]=\frac{u_2}{2}$}, {$[\frac{u_1}{2},\frac{u_2}{2}]=\frac{u_3}{2}$}, {$[\frac{u_2}{2},\frac{u_3}{2}]=\frac{u_1}{2}$}.

Imaginary number expresses non-matching. Three ways of expressing non-matching: blank 1 with symbol i; two symbols matching ++ or not matching +-; self-matching ii or self-non-matching ij. Three-cycle expresses non-matching.

The Lie bracket (more specifically, the commutator) expresses duality in that it matches a positively weighted term {$xy$} with a negatively weighted term {$-yx$} and so it is robustly nonzero precisely when this duality of left-to-right vs. right-to-left is most explicit.

Correspondence of real Lie algebra and compact Lie group

Lie group - Lie algebra correspondence

{$\mathrm{Lie}(G)=\{X\in M(n;\mathbb{C})|e^{tX}\in G \text{ for all } t \in \mathbb{R}\}$}

Example:

{$\mathfrak{su}(2) \Leftrightarrow \text{SU}(2)$}

The special unitary group consists of all unitary matrices with determinant {$1$}.

{$\begin{pmatrix} c_{11} & c_{12}\\ -\overline{c_{12}} & \overline{c_{11}} \end{pmatrix}$} where {$c_{11}\overline{c_{11}}+c_{12}\overline{c_{12}}=1$}

Basis elements of {$\frak{su}(2)$} yield basis elements of {$\text{SU}(2,\mathbb{C})$} as follows:

{$e^{t_1i\begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}}=I\,\text{cos}\, t_1 + i{\begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}}\text{sin}\, t_1 = {\begin{pmatrix} \text{cos}\, t_1 + i \, \text{sin}\, t_1 & 0\\ 0 & \text{cos}\, t_1 - i \, \text{sin}\, t_1 \end{pmatrix}}$} {$$ = {\begin{pmatrix} e^{it_1} & 0\\ 0 & e^{-it_1} \end{pmatrix}}$$}

{$e^{t_2i\begin{pmatrix} 0 & i\\ -i & 0 \end{pmatrix}}=I\,\text{cos}\, t_2 + i{\begin{pmatrix} 0 & i\\ -i & 0 \end{pmatrix}}\text{sin}\, t_2 = {\begin{pmatrix} \text{cos}\, t_2 & -\text{sin}\, t_2 \\ \text{sin}\, t_2 & \text{cos}\, t_2 \end{pmatrix}}$}

{$e^{t_3i\begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix}}=I\,\text{cos}\, t_3 + i{\begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix}}\text{sin}\, t_3 = {\begin{pmatrix} \text{cos}\, t_3 & i \, \text{sin}\, t_3 \\ i \, \text{sin}\, t_3 & \text{cos}\, t_3 \end{pmatrix}}$}

Note that an additive subgroup of {$\frak{su}(2)$} (generated by a basis element) corresponds to a multiplicative subgroup of {$\text{SU}(2,\mathbb{C})$} (generated by a generator).

Note that, when we take the determinant, the three basis elements construct the term {$\text{sin}^2t$} in three different ways: {$i\times-i$}, {$-(-1 \times 1)$}, {$-(i\times i)$}.

We can study the general expression:

{$e^{t_1i\begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}+t_2i\begin{pmatrix} 0 & i\\ -i & 0 \end{pmatrix}+t_3i\begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix}}$}

But we must take care because {$e^{A+B}=e^Ae^B$} generally only when {$A$} and {$B$} commute, that is, {$[A,B]=0$}. In general, we can use the Baker–Campbell–Hausdorff formula.

{$\mathfrak{su}(2)=\{X\in M(n;\mathbb{C})|e^{tX}\in \text{SU}(2) \text{ for all } t \in \mathbb{R}\}$}

Correspondence of complex Lie algebra and complex Lie group

Example:

{$\mathfrak{sl}(2,\mathbb{C}) \Leftrightarrow \text{SL}(2,\mathbb{C})$}

Basis elements of {$\frak{sl}(2)$} yield basis elements of {$\text{SL}(2,\mathbb{C})$} as follows:

{$e^{t_1\begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}}=I\,\text{cosh}\, t_1 + {\begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}}\text{sinh}\, t_1 = {\begin{pmatrix} \text{cosh}\, t_1 + \text{sinh}\, t_1 & 0\\ 0 & \text{cosh}\, t_1 - \text{sinh}\, t_1 \end{pmatrix}}$} {$$ = {\begin{pmatrix} \text{cos}\, t_1 \, i + i \, \text{sin}\, t_1 i & 0\\ 0 & \text{cos}\, t_1 i - i \, \text{sin}\, t_1 i \end{pmatrix}}$$} {$$ = {\begin{pmatrix} e^{t_1} & 0\\ 0 & e^{-t_1} \end{pmatrix}}$$}

{$e^{t_2\begin{pmatrix} 0 & 1\\ 0 & 0 \end{pmatrix}}={\begin{pmatrix} 1 & t_2\\ 0 & 1 \end{pmatrix}}$}

{$e^{t_3\begin{pmatrix} 0 & 0\\ 1 & 0 \end{pmatrix}}={\begin{pmatrix} 1 & 0\\ t_3 & 1 \end{pmatrix}}$}

In the Lie algebra {$\mathfrak{su}(2)$}:

{$\left [{\begin{pmatrix} t_1 & 0\\ 0 & -t_1 \end{pmatrix}} , {\begin{pmatrix} 0 & t_2\\ 0 & 0 \end{pmatrix}} \right ] = {\begin{pmatrix} 0 & t_1t_2\\ 0 & 0 \end{pmatrix}} - {\begin{pmatrix} 0 & -t_2t_1\\ 0 & 0 \end{pmatrix}} = {\begin{pmatrix} 0 & t_1t_2+t_2t_1\\ 0 & 0 \end{pmatrix}}$}

{$\left [{\begin{pmatrix} 0 & t_2\\ 0 & 0 \end{pmatrix}} , {\begin{pmatrix} 0 & 0\\ t_3 & 0 \end{pmatrix}} \right ] = {\begin{pmatrix} t_2t_3 & 0\\ 0 & 0 \end{pmatrix}} - {\begin{pmatrix} 0 & 0\\ 0 & -t_3t_2 \end{pmatrix}} ={\begin{pmatrix} t_2t_3 & 0\\ 0 & -t_3t_2 \end{pmatrix}}$}

We can thus accordingly define, within the Lie group {$\mathrm{SU}(2)$}:

{$\left [{\begin{pmatrix} e^{t_1} & 0\\ 0 & e^{-t_1} \end{pmatrix}} , {\begin{pmatrix} 1 & t_2\\ 0 & 1 \end{pmatrix}} \right ] = {\begin{pmatrix} 1 & t_1t_2+t_2t_1\\ 0 & 1 \end{pmatrix}} $}

{$\left [{\begin{pmatrix} 1 & t_2\\ 0 & 1 \end{pmatrix}} , {\begin{pmatrix} 1 & 0\\ t_3 & 1 \end{pmatrix}} \right ] = {\begin{pmatrix} e^{t_2t_3} & 0\\ 0 & e^{-t_3t_2} \end{pmatrix}} $}

Note that within the group, the Lie bracket functions multiplicatively. Note that the multiplication gets expressed dually. In the case of {$e^H$} that duality is expressed noncomparatively. In the case of {$e^X$}, that duality is expressed in terms of comparable terms.

In general, we have the volume-preserving (determinant equals one) formulas:

{${\begin{pmatrix} 1 & t\\ 0 & 1 \end{pmatrix}}{\begin{pmatrix} 1 & s\\ 0 & 1 \end{pmatrix}}={\begin{pmatrix} 1 & t+s\\ 0 & 1 \end{pmatrix}} $}

{${\begin{pmatrix} 1 & 0\\ t & 1 \end{pmatrix}}{\begin{pmatrix} 1 & 0\\ s & 1 \end{pmatrix}}={\begin{pmatrix} 1 & 0\\ t+s & 1 \end{pmatrix}} $}

{${\begin{pmatrix} e^t & 0\\ 0 & e^{-t} \end{pmatrix}}{\begin{pmatrix} e^s & 0\\ 0 & e^{-s} \end{pmatrix}} = {\begin{pmatrix} e^{t+s} & 0\\ 0 & e^{-t-s} \end{pmatrix}} $}

Thus we have three natural copies of {$\mathbb{R}$} as multiplicative subgroups of {$\mathrm{SL}(2,\mathbb{C})$}. (Are these the only three such subgroups? How do we prove that?) And these three subgroups are related by the Lie bracket. Each subgroup can be thought of as a rotation minus the point at infinity. Thus {$e^t$} expresses that rotation internally and the triangular matrices express it externally. If we have {$e^{it}$}, then the rotation is expressed in terms of a circle and is periodic. The way that complex numbers combine rotations with and without the point at infinity is similar to the way that a ring combines groups with zero (additive) and without zero (multiplicative).

Complexification of compact Lie group

The complexification is given by elements {$g=u \cdot e^{iX}$} where {$u$} is a unitary operator in the compact group, and {$X$} is a skew-adjoint operator of its Lie algebra.

Note: Compute this for the basis of {$\frak{su}(2)$}.

The complexification is {$\mathrm{SL}(n,\mathbb{C})$} and the compact group is {$\mathrm{SU}(n)$}.

A matrix is skew-Hermitian or skew-adjoint if its conjugate transpose is the negative of the original matrix. In this case we have:

{$–\begin{pmatrix} a_{11}+ib_{11} & a_{12}+ib_{12} \\ a_{21}+ib_{21} & a_{22}+ib_{22} \end{pmatrix} = \begin{pmatrix} a_{11}-ib_{11} & a_{21}-ib_{21} \\ a_{12}-ib_{12} & a_{22}-ib_{22} \end{pmatrix}$}

Thus the matrices of {$\frak{u}(n)$} have the form

{$\begin{pmatrix} ib_{11} & a_{12}+ib_{12} \\ -a_{12}+ib_{12} & ib_{22} \end{pmatrix}$}

in other words:

{$i\begin{pmatrix} b_{11} & z_{12} \\ \bar{z}_{12} & b_{22} \end{pmatrix}$}

The matrices of {$\frak{su}(n)$} have the form

{$iB=i\begin{pmatrix} b & z \\ \bar{z} & -b \end{pmatrix}$}

The set of all skew-Hermitian (in other words, skew-adjoint) {$n × n$} matrices forms the {$\frak{u}(n)$} Lie algebra, which corresponds to the Lie group {$\mathrm{U}(n)$}. Skew-Hermitian matrices with trace {$0$} form the {$\frak{su}(n)$} Lie algebra, which corresponds to the Lie group {$\mathrm{SU}(n)$}, whose elements have determinant {$1$}.

Note that {$\textrm{det}(-B)=b^2+|z|^2$}. Call this {$|-B|$}.

Note that {$B^2 = \begin{pmatrix} b^2+|z|^2 & 0 \\ 0 & b^2+|z|^2 \end{pmatrix}=(b^2+|z|^2)I=|-B|I$}

Make use of the Taylor series expansions

{$$\textrm{cos}(iX)= \textrm{cosh}(X)=1+X^2/2!+\cdots$$}

{$$-i\textrm{sin}(iX)=\textrm{sinh}(X)=X+X^3/3!+\cdots$$}

We have {$e^{i\cdot iB}=e^{-B}= \textrm{cosh}(|-B|)I-\textrm{sinh}(|-B|)B$}.

Why isn't determinant of the resulting matrix equal to 1? Calculate the eigenvalues of {$iB$} and of {$e^{-B}$}. study this

Unitary group

The unitary matrices in {$\textrm{U}(2)$} look like this:

{$\begin{pmatrix} x & 0 \\ 0 & \overline{x} \end{pmatrix} + i \begin{pmatrix} 0 & \overline{y} \\ y & 0 \end{pmatrix} $}

Special linear group

Multiplying them together should yield the special linear group.