Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

Learning the Yoneda Lemma

The Yoneda Lemma is the fundamental theorem of category theory.

The Yoneda Lemma is the framework for defining the number zero, which is to say, for defining the identity element, the action of doing nothing.

I personally am studying the Yoneda Lemma to thoroughly understand its meaning and how that relates to my philosophical, especially describing the levels of knowledge: whether, what, how, why.

I share my understanding that I am developing.

Here is the statement.

This is a difficult, abstract, terse, deep result.

I will develop the idea of the Yoneda Lemma through a series of generalizations.

Two ways of looking at the same thing

The Yoneda Lemma establishes a natural isomorphism. This means that it relates two different ways of looking at the same thing.

The germ of the Yoneda Lemma

The Yoneda Lemma generalizes the fact that the following two statements are equivalent:

1) You can keep up with me.

2) Take anybody, if I can keep up with them, then you can keep up with them, too.

Suppose 1). If I can keep up with somebody, then since you can keep up with me, it follows that you can keep up with them. This gives 2).

Suppose 2). Note that I can keep up with myself. Thus you can keep up with me. This gives 1).

We may term these the direct formulation 1) and the universal formulation 2).

A fact about preorders

Let's write this out mathematically.

A preorder is a binary relation that is reflexive {$a\leq a$} and transitive {$a\leq b \wedge b\leq c \Rightarrow a\leq c$}. An example is the natural numbers.

The Yoneda Lemma is a generalization of the following fact about preorders.

{$y\leq x$} iff {$(\forall z)(z\leq y \Rightarrow z\leq x)$}

From left to right, we use transitivity: If {$y\leq x$} and {$z\leq y$}, then {$z\leq x$}.

From right to left, we instantiate {$z$} to {$y$}, and use reflexivity: {$y\leq y$}, thus {$x\leq y$}.

Thus we have two ways of looking at the same fact. We may focus on the particular relation between {$x$} and {$y$}, or we can consider the general correlation in their relationships with every {$z$}.

Transitivity takes us from the particular relation to the general correlation. Instantiation and reflexivity take us from the general correlation to the particular relation.

Note that it is crucial for reflexivity that the relation be weakly increasing and not strictly increasing. This distinction is critical for the Yoneda lemma because it leverages reflexivity.

Why these shifts in perspective?

A category is more than just objects and arrows (which might be modeled by a labeled diagram or a matrix). It also includes constraints, namely identity arrows (like an identity matrix), and composition (like matrix multiplication).

The arrows in a category are related by this highly complex relationship which can be assumed implicitly, by composition, or written out explicitly, by logical implication. We can use transitivity to make composition explicit as implication. Or we can suppress the logical notation by collapsing the pertinent arrow to be the identity morphism, which need not be mentioned.

When we write y <= x (or x->y) as an Arrow, then those constraints are implicit as composition rules. Alternatively, we can spell out the constraints explicitly as logical implications, indexed by the objects z, thus defining a Natural transformation.

Note that the universal quantifier {$\forall z$} is at the root of the natural transformation. And the existential quantifier {$\exists z(z=y)$} is at the root of the instantiation.

Note the significance of the identity morphism. It assures the existence of the needed morphism, and without it, the system may be empty, may collapse away. This is a point where it is consequential whether our system is empty or not, and that distinction comes up in my philosophy's take on logic. For example, the meaning of the statement "you owe me money" depends on whether or not it is possible to owe somebody zero money. Implicitly, one never owes somebody zero money, but explicitly they can. The number zero makes no sense implicitly, but is essential punctuation in an explicit system.

Thus the statement is perhaps cognitively more explicit written as:

{$y\leq x$} iff {$(\forall z)(0\leq (y-z) \Rightarrow 0\leq (x-z))$}

Also, an explicit perspective, where statements are written out, statically, is one that applies memory, as with pushdown automata. Whereas an implicit perspective is dynamic as with the execution of a program, as with a finite automata.

Expressing with diagrams

Note that every preorder may be thought of as a category where {$y\leq x$} is understood as the arrow {$X\rightarrow Y$}. We can express the logical statement as a diagram:

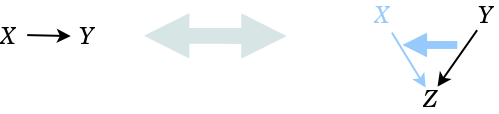
Going from left to right, we apply composition to prepend {$X\rightarrow Y$}.

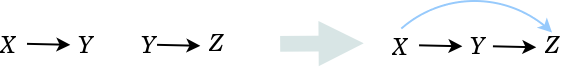
Going from right to left, we apply instantiation {$Z=Y$} and use implication.

In summary, we have two perspectives ... what are they?

We go left to right by general composition and then specific implication. We go from right to left by general implication and specific instantiation.

So on the left side we have a perspective in terms of implied composition, and on the right side we have a perspective of explicit implication.

Thus going from left to right makes the composition explicit as implication, and going from right to left makes the implication implicit as composition. In the case of composition, we needn't show the context, whereas in the case of implication, the context is always shown.

The Hom sets

A preorder is a category {$\mathbf{C}$} in which there is at most one arrow between any two objects {$X$} and {$Y$}, where we may have {$X=Y$}. In other words, the set of arrows between {$X$} and {$Y$}, denoted {$\textrm{Hom}(X,Y)$}, has at most one element. We can then write our logical statement as:

{$\textrm{Hom}(X,Y)\neq \varnothing \Leftrightarrow \forall Z (\textrm{Hom}(Y,Z)\neq \varnothing \Rightarrow \textrm{Hom}(X,Z) \neq \varnothing )$}

Note that {$\textrm{Hom}(Y,Z)$} and {$\textrm{Hom}(X,Z)$} are sets. The right hand side of the logical statement can be thought of as stating that a set function exists, where that function may possibly be the empty function, having an empty domain.

{$\textrm{Hom}(X,Y)\neq \varnothing \Leftrightarrow \forall Z (\exists f:\textrm{Hom}(Y,Z)\rightarrow \textrm{Hom}(X,Z))$}

{$\forall Z$} is a universal quantifier over the objects {$Z$} in {$\mathbf{C}$}. Thus it may possibly index the components of a natural transformation.

We may think of {$\textrm{Hom}(Y,Z)$} and {$\textrm{Hom}(X,Z)$} as functors in {$Z$} from {$\mathbf{C}$} to {$\textbf{Set}$}. Let us denote them {$\textrm{Hom}_\mathbf{C}(Y,\_)$} and {$\textrm{Hom}_\mathbf{C}(X,\_)$}. For example, {$\textrm{Hom}_\mathbf{C}(Y,\_)$} takes input {$Z$} in {$\mathbf{C}$} and outputs the set {$\textrm{Hom}_\mathbf{C}(Y,Z)$}. Note that for any arrow {$g:A\rightarrow B$} we have the commutativity diagram:

{$$ \matrix{\textrm{Hom}_\mathbf{C}(Y,A) & \overset{f_{*A} \textrm{ prepends } f:X\rightarrow Y}{\longrightarrow} & \textrm{Hom}_\mathbf{C}(X,A) \cr \scriptsize\textrm{Hom}_\mathbf{C}(Y,\_)(g) \textrm{ postpends } g:A\rightarrow B \bigg\downarrow & & \bigg\downarrow \scriptsize\textrm{Hom}_\mathbf{C}(X,\_)(g) \textrm{ postpends } g:A\rightarrow B \cr \textrm{Hom}_\mathbf{C}(Y,B) & \underset{f_{*B} \textrm{ prepends } f:X\rightarrow Y}{\longrightarrow} & \textrm{Hom}_\mathbf{C}(X,B) \cr } $$}

It doesn't matter in what order we prepend {$g$} and postpend {$f$}. Thus the pullback {$f_*$} is a natural transformation from {$\textrm{Hom}(Y,\_)$} to {$\textrm{Hom}(X,\_)$}.

Thus we can write:

{$\textrm{Hom}(X,Y)\neq \varnothing \Leftrightarrow \textrm{Hom}(\textrm{Hom}(Y,\_), \textrm{Hom}(X,\_)) \neq \varnothing$}

The set on the left is nonempty, then it contains a single element {$f:X\rightarrow Y$}. Then the set on the right contains {$f_*$}. But could it contain more elements? The answer is no, as we can see by studying the Yoneda embedding.

The Yoneda embedding

The Yoneda embedding is a functor {$\mathcal Y:\mathbf{C}\rightarrow \mathbf{Set}^{\mathbf{C}}$} that sends an object {$X$} to the functor {$\textrm{Hom}(X,\_)$} and sends a function {$f:X\rightarrow Y$} to the natural transformation {$f_{*}:\textrm{Hom}(Y,\_)\rightarrow \textrm{Hom}(X,\_)$} whose component {$f_{*Z}$} is the set function which prepends {$f$} to an element of {$\textrm{Hom}(Y,Z)$} to get an element {$\textrm{Hom}(X,Z)$}.

The Yoneda embedding is faithful

Clearly, the Yoneda embedding is a faithful functor. If {$f,g:X\rightarrow Y$} and {$f\neq g$}, then {$f_*\neq g_*$}. Here we need to note that at least one input exists, namely, {$\textrm{id}_Y$} exists and consequently {$f_*(\textrm{id}_Y)=f\neq g=g_*(\textrm{id}_Y)$}.

The Yoneda embedding is full

We can show that the Yoneda embedding is also a full functor, which is to say, every natural transformation {$\theta:\textrm{Hom}(Y,\_)\rightarrow \textrm{Hom}(X,\_)$} is of the form {$\theta = g_{*}$} for some {$g:X\rightarrow Y$}.

Given any object {$B$} in {$\mathbf{C}$}, then the component {$\theta_B$} has domain {$\textrm{Hom}(Y,B)$}. Let the element {$f:Y\rightarrow B$} be an arrow in that domain. Then consider the commutativity diagram which relates {$\theta$} and {$f$}, and note its action on the input {$\textrm{id}_Y\in \textrm{Hom}_{\mathbf{C}}(Y,Y)$}:

{$$ \matrix{\textrm{id}_Y\in\textrm{Hom}_\mathbf{C}(Y,Y) & \overset{\theta_Y}{\longrightarrow} & \theta_Y(\textrm{id}_Y)\in\textrm{Hom}_\mathbf{C}(X,Y) \cr \scriptsize\textrm{Hom}_\mathbf{C}(Y,\_)(f) \textrm{ postpends } f:Y\rightarrow B \bigg\downarrow & & \bigg\downarrow \scriptsize\textrm{Hom}_\mathbf{C}(X,\_)(f) f\in\textrm{ postpends } f:Y\rightarrow B \cr f\in\textrm{Hom}_\mathbf{C}(Y,B) & \underset{\theta_B}{\longrightarrow} & \theta_B(f)=f\circ\theta_Y(\textrm{id}_Y)\in\textrm{Hom}_\mathbf{C}(X,B) \cr } $$}

Here {$\textrm{Hom}(Y,\_)$} is the functor which postpends {$f:Y\rightarrow B$}, in this case, to the arrow {$\textrm{id}_Y$}. Postpending {$f$} to {$\textrm{id}_Y$} yields {$f$}. Similarly, {$\textrm{Hom}(Y,\_)$} is the functor which postpends {$f:Y\rightarrow B$}, in this case, to {$\theta_{Y}(\textrm{id}_Y):X\rightarrow Y$}, yielding {$f\circ \theta_{Y}(\textrm{id}_Y):X\rightarrow B$}. Thus we conclude from the commutative diagram that {$\theta_B(f)=f\circ \theta_{Y}(\textrm{id}_Y)$}.

This means that the natural transformation {$\theta$} is determined by where {$\theta_Y$} sends {$\textrm{id}_Y$}. Specifically, every natural transformation {$\theta:\textrm{Hom}(Y,\_)\rightarrow \textrm{Hom}(X,\_)$} simply prepends the arrow {$\theta_{Y}(\textrm{id}_Y):X\rightarrow Y$} to input {$f$} to yield its output {$f\circ \theta_{Y}(\textrm{id}_Y):X\rightarrow B$}.

Thus the Yoneda embedding functor {$\mathcal Y:X\rightarrow \textrm{Hom}(X,\_)$} is full. It is also faithful, thus it is fully faithful.

The Yoneda embedding bijection

In particular, there is a bijection between arrows {$f:X\rightarrow Y$} and natural transformations {$f_*:\textrm{Hom}(Y,\_)\rightarrow \textrm{Hom}(X,\_)$} where {$f=f_{*Y}(\textrm{id}_Y)$}. We can write:

{$\textrm{Hom}(X,Y) \leftrightarrow \textrm{Hom}(\textrm{Hom}(Y,\_), \textrm{Hom}(X,\_))$}

Expressing with diagrams

We can express the Yoneda embedding bijection with diagrams. When the category is a preorder, then there is at most one morphism between any two objects, but now, in the general case, we have to label the morphisms.

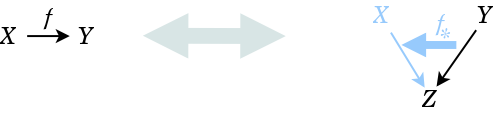
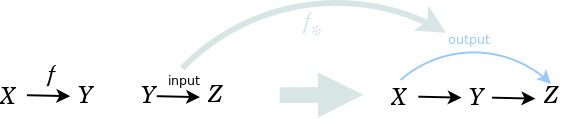
The diagrams make clear that the natural transformation {$f_*$} postpends an input arrow to {$f$} to yield an output arrow. And when {$f_*$} receives, as input, the null arrow (the identity morphism), then it outputs {$f$}.

This means that, in general, we can understand {$f_*$} as taking its input {$g:Y\rightarrow Z$} and dividing it up into two parts as {$g = g\circ \textrm{id}_Y$}. It sends the first "do nothing" part {$\textrm{id}_Y$} to {$f$} and the second "do something" part {$g$} to {$g$}, and thus in combination sending {$g$} to {$g\circ f$}. Note that this reconstruction of two arrows from one arrow mirrors how composition merges two arrows into one arrow. The reconstruction crucially depends on using the identity arrow and mapping it to a general prefix.

Note

It's important to note that {$\textrm{Hom}(\textrm{Hom}(Y,\_), \textrm{Hom}(X,\_))$} is the set of natural transformations. The components of such a natural transformation are set functions. However, there are many set functions between hom sets that are not components of any natural transformation.

The bijection in Cayley's theorem: {$f:\bigcirc\rightarrow\bigcirc$} is a group element and {${f_*}_{\bigcirc}$} is a corresponding permutation

Now we can consider what the Yoneda embedding bijection means for particular categories.

Consider a group {$\mathbf{G}$} as a category which consists of a single object {$\bigcirc$}, where the elements are the morphisms, and where composition accords with the multiplication of elements.

Such a category is an example where the morphisms are of complete interest, and the objects are of no interest.

Then {$\textrm{Hom}(\bigcirc,\bigcirc)$} is the set of elements of the group.

The functor {$\textrm{Hom}(\bigcirc,\_):\mathbf{C}\rightarrow \mathbf{Set}$} maps the object {$\bigcirc$} to that set of elements {$\textrm{Hom}(\bigcirc,\bigcirc)$}. It maps a morphism, that is, a group element {$g$} to the set function {$\textrm{Hom}(\bigcirc,\_)(g)$} which is the action that maps any element {$h$} to the element {$gh$}, which is to say, the action which postpends {$g$}.

What are the natural transformations {$\theta$} which map this functor {$\textrm{Hom}(\bigcirc,\_)$} to itself?

Such a {$\theta$} has a single component {$\theta_\bigcirc$} because {$\mathbf{G}$} has a single object {$\bigcirc$}. As we have seen earlier, there exists an {$f\in\textrm{Hom}(\bigcirc,\bigcirc)$} such that {$\theta=f_*$} where {${f_*}_{\bigcirc}(\textrm{id}_{\bigcirc})=f$}. Note here that {$e=\textrm{id}_{\bigcirc}$} is the group's identity element.

Given a morphism {$g:\bigcirc\rightarrow\bigcirc$}, we have the following commutativity diagram.

{$$ \matrix{h\in\textrm{Hom}_\mathbf{G}(\bigcirc,\bigcirc) & \overset{\theta_\bigcirc={f_*}_{\bigcirc} \textrm{ prepends } f:\bigcirc\rightarrow\bigcirc}{\longrightarrow} & \theta_\bigcirc(h)=hf\in\textrm{Hom}_\mathbf{G}(\bigcirc,\bigcirc) \cr \scriptsize\textrm{Hom}_\mathbf{G}(\bigcirc,\_)(g) \textrm{ postpends } g:\bigcirc\rightarrow\bigcirc \bigg\downarrow & & \bigg\downarrow \scriptsize\textrm{Hom}_\mathbf{G}(\bigcirc,\_)(g) \textrm{ postpends } g:\bigcirc\rightarrow\bigcirc \cr gh\in\textrm{Hom}_\mathbf{G}(\bigcirc,\bigcirc) & \underset{\theta_\bigcirc={f_*}_{\bigcirc} \textrm{ prepends } f:\bigcirc\rightarrow\bigcirc}{\longrightarrow} & \theta_\bigcirc(gh)=g\theta_\bigcirc(h)=ghf\in\textrm{Hom}_\mathbf{G}(\bigcirc,\bigcirc) \cr } $$}

Thus for any morphism {$g$} and set function input {$h\in \textrm{Hom}(\bigcirc,\bigcirc)$} we have {$\theta_{\bigcirc}(gh)=g\theta_{\bigcirc}(h)$}. In particular, for input {$e=\textrm{id}_{\bigcirc}$}, the identity element, we have {$\theta_{\bigcirc}(g)=g\theta_{\bigcirc}(\textrm{id}_{\bigcirc})$}. As we saw before, the value {$\theta_{\bigcirc}(\textrm{id}_{\bigcirc})=f$} determines the natural transformation {$\theta=f_*$}, so that {${f_*}_{\bigcirc}(g)={f_*}_{\bigcirc}(g\;\textrm{id}_{\bigcirc})=g{f_*}_{\bigcirc}(\textrm{id}_{\bigcirc})=gf$}.

Each natural transformation {$f_*$} in {$\textrm{Hom}(\textrm{Hom}(\bigcirc,\_),\textrm{Hom}(\bigcirc,\_))$} is a family consisting of a single component, a set function {${f_*}_{\bigcirc}:\textrm{Hom}(\bigcirc,\bigcirc)\rightarrow \textrm{Hom}(\bigcirc,\bigcirc)$}, which is a system of equations where {${f_*}_{\bigcirc}:h\rightarrow hf$} for all {$h\in\textrm{Hom}(\bigcirc,\bigcirc)$} where {$f$} is prepended.

{${f_*}_{\bigcirc}$} is injective because {$f^{-1}$} exists, thus {${f_*}_{\bigcirc}(h)={f_*}_{\bigcirc}(g)\Rightarrow {f_*}_{\bigcirc}(h\; \textrm{id}_{\bigcirc})={f_*}_{\bigcirc}(g\;\textrm{id}_{\bigcirc}) \Rightarrow h{f_*}_{\bigcirc}(\textrm{id}_{\bigcirc})=g{f_*}_{\bigcirc}(\textrm{id}_{\bigcirc}) \Rightarrow hf=gf \Rightarrow hff^{-1}=gff^{-1} \Rightarrow h=g$}.

{${f_*}_{\bigcirc}$} is surjective likewise because {$f^{-1}$} exists. For any element {$g$} there is an element {$gf^{-1}\textrm{id}_{\bigcirc}$} such that{${f_*}_{\bigcirc}(gf^{-1}\textrm{id}_{\bigcirc}) = gf^{-1}{f_*}_{\bigcirc}(\textrm{id}_{\bigcirc}) = gf^{-1}f = g$}.

Thus the set function {${f_*}_{\bigcirc}$} is an automorphism, a permutation of the set {$\textrm{Hom}(\bigcirc,\bigcirc)$}, which is the set of elements of {$\mathbf{G}$}.

Cayley's theorem: the group {$\mathbf{G}$} is isomorphic to a group of permutations

The Yoneda embedding {$\eta :\textrm{Hom}(\bigcirc,\bigcirc) \rightarrow \textrm{Hom}(\textrm{Hom}(\bigcirc,\_), \textrm{Hom}(\bigcirc,\_))$} sends the element {$f$} to the natural transformation {${f_*}$}. We know that {$\eta$} is injective and that also all natural transformations in {$\textrm{Hom}(\textrm{Hom}(\bigcirc,\_), \textrm{Hom}(\bigcirc,\_))$} are of the form {$f_*$} for some arrow {$f$} in {$\mathbf{G}$}, which is to say, for some group element {$f$}.

We want to show that here the Yoneda embedding is not just a bijection but is, in fact, a group homomorphism. In our notation the composition gets inverted and we want to show that {$\eta(fg)=(fg)_*=g_*f_*=\eta(g)\eta(f)$}. Note that {$\eta(g)\eta(f)$} is vertical composition of two natural transformations of the functor {$\textrm{Hom}(\bigcirc,\_):\mathbf{G}\rightarrow\mathbf{Set}$} to itself, and that vertical composition takes place componentwise. There is one object {$\bigcirc$} and thus one component. We see that:

{$a\in\textrm{Hom}(\bigcirc,\bigcirc)\overset{{(fg)_*}_{\bigcirc} \textrm{ prepends } fg:\bigcirc\rightarrow\bigcirc}{\rightarrow}afg\in\textrm{Hom}(\bigcirc,\bigcirc)$}

is the same as:

{$a\in\textrm{Hom}(\bigcirc,\bigcirc)\overset{{(f)_*}_{\bigcirc} \textrm{ prepends } f:\bigcirc\rightarrow\bigcirc}{\rightarrow}af\in\textrm{Hom}(\bigcirc,\bigcirc)\overset{{(g)_*}_{\bigcirc} \textrm{ prepends } g:\bigcirc\rightarrow\bigcirc}{\rightarrow}afg\in\textrm{Hom}(\bigcirc,\bigcirc)$}

Thus {${(fg)_*}_{\bigcirc}$} is the same as {${g_*}_{\bigcirc}{f_*}_{\bigcirc}$}. In general, {${(fgh)_*}_{\bigcirc}={h_*}_{\bigcirc}{g_*}_{\bigcirc}{f_*}_{\bigcirc}$}, and the composition is associative.

We have interpreted the Yoneda embedding to be the desired group homomorphism.

The Yoneda embedding is injective and so we have a group isomorphism. The image of this group homomorphism is the desired group of permutations.

Why the inversion?

The composition of group elements {$fg$} is conventionally understood as a string read from left to right. It is then reinterpreted as a composition of functions {$g(f(\;))$} which is conventionally read from right to left. The inversion is apparently the result of convention. Or is there a deeper reason?

Levels of knowledge

Cayley's theorem helps us distinguish the ways that we think about a group element {$f$}. I believe these reflect levels of knowledge: Whether, What, How, Why.

• Whether (a noun): {$f:\bigcirc\rightarrow\bigcirc$} is an arrow in the category {$\mathbf{G}$}
• What (an adjective, a modifier, an extension): {$f$} is a modifier of the identity element {$\textrm{id}_{\bigcirc}$}. {$f$} is an element of {$\textrm{Hom}(\bigcirc,\bigcirc)$}. The latter set is the application of the functor to {$\bigcirc$} and implicitly uses {$\textrm{id}_{\bigcirc}$} to identify the internal {$\bigcirc$} with the input {$\bigcirc$}. {$f$} is interpreted as a combination {$\textrm{id}_{\bigcirc}\;f$} where {$f$} modifies this identity element by prepending itself.
• How (a verb, an action, a system of equations): {${f_*}_{\bigcirc}:\textrm{Hom}(\bigcirc,\bigcirc)\rightarrow\textrm{Hom}(\bigcirc,\bigcirc)$} is a component of {${f_*}$} with a commutativity diagram in {$\mathbf{Set}$} that is indexed by {$\bigcirc$}. {${f_*}_{\bigcirc}$} is a set function, and as such, a system of equations {${f_*}_{\bigcirc}:h\rightarrow hf$} indexed by the objects {$h$} of {$\mathbf{G}$}, where each equation describes how {${f_*}_{\bigcirc}$} prepends {$f$} to any particular element {$h$} of the group.
  • Similarly, {$\textrm{Hom}(\bigcirc,\_)(f)$} is a set function that takes {$a\in\textrm{Hom}(\bigcirc,\bigcirc)$} to {$fa\in\textrm{Hom}(\bigcirc,\bigcirc)$}, which is to say, it postpends {$f$} to any input {$a$}.
• Why: (a symmetry, a transformation) {$f_*$} is a natural transformation from the functor {$\textrm{Hom}(\bigcirc,\_)$} to itself which manifests a global symmetry, a global invariance of the structure, whereby the action in {$\mathbf{G}$} of prepending with the arrow {$f$} is compatible with any action in {$\mathbf{G}$} of postpending with an arrow {$g$}.

Wenbo's observation

{$Nat(A\_,\_)\rightarrow F_ \cong FA$}

{$\forall b ((a\rightarrow b)\rightarrow Fb) \cong Fa $}

{$\forall b (a\rightarrow b)\rightarrow b) \cong a $} choosing {$F=I$}

{$a(a\rightarrow I) \rightarrow I) \cong a$} choosing {$b=I$}

Notes to self:

• If the identity morphism is taken as a type, then the arrow becomes the modifier that distinguishes it. Each object is a type and the arrows are typed by the object they are coming from.
• Consider the role of context: How is within context, Why is outside of context. The perspective in terms of composition has implicit context, whereas for implication the context is explicit.
• How expresses composition by which two become one. What expresses reflexivity and instantiation by which one becomes two.
• Why sets up the duality of postpending and prepending which defines the outer system and the inner subsystem.

---

Univalence Axiom

How is the Yoneda Lemma related to the univalence axiom?

Notes

• Composition combines one symmetry with another symmetry to yield a third symmetry.
• Wenbo: Serialization, object oriented ontology, (a->I)->I = a, double negative, Computational type theory - Robert Harper - OPLSS 2018, nyc-category-theory.slack.com
• Distinction between type (the identity morphism) and its qualifier (token?). Why and whether are arrows, wheras how is composition? and what is factoring?
• Duality of factoring (forgetful, not knowing) and composition (free, knowing).

Thoughts and notes...

The category {$\mathbf{Set}$} is based on asymmetry in that it has one terminal object, the empty set {$\varnothing$}, but many initial objects, the singletons {$\{a\}$}.

How is the natural transformation a relabeling?

https://math.stackexchange.com/questions/1701/yoneda-lemma-as-generalization-of-cayleys-theorem

https://mathoverflow.net/questions/27971/why-is-there-no-cayleys-theorem-for-rings

Know the purpose

• Relates internal structure and external relationships.
• Leverages the category Set.
• Allows the embedding of any category into a category of functors (contravariant set-valued functors) defined on that category.

Understand it top down

• Given: an object {$A$} in a category {$C$} and a functor {$F:C\rightarrow Set$}.
• It is a set isomorphism.
• But more than that, it is a natural transformation that relates two functors from {$Set^C \times C$} to {$Set$}.
• In other words, it is a natural transformation that relates two functors that are objects in the functor category {$Set^{Set^C \times C}$}.

Calculate bottom up

• Eduardo Och's internal diagram.

Understand concrete examples

• Cayley's theorem for groups.
• Richard Southwell's example of graphs.
• Richard Southwell's example of dynamical systems.

Understand how it is generalized

• Understand how Kan extensions are used to generalize the Yoneda lemma.

Understand how it is used in theorems

Understand it cognitively

• I want to understand what is says about levels of knowledge: Whether, What, How, Why.

Attach:YonedaLemmaExposition-650.png Δ

Acknowledgements

Thank you to Robert Harper for alerting me that the Yoneda Lemma is a generalization of the fact about preorders.