Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

Understanding

• Most relevant for me is the Yoneda Embedding.
• Yoneda Embedding describes a knowledge switch. A switch that controls mental movement.
• The shift from How-What to Why-Whether adds context.
• Whether builds up knowledge. The shift from Why to Whether converts consciousness into knowledge. (As with eternalization in the sixsome of emotions into virtues.)
• Whether relates How and What and thus builds knowledge as relationships.
• Why expresses the constraints of the global quantum and Whether the assembling of the local quantum.
• Context creates knowledge.
• The slot in the homsets is the space that opens up for a decision point in the fivesome.
• In the Yoneda lemma, the foursome is a context for the indefinite, for the nullsome, which is the slot.

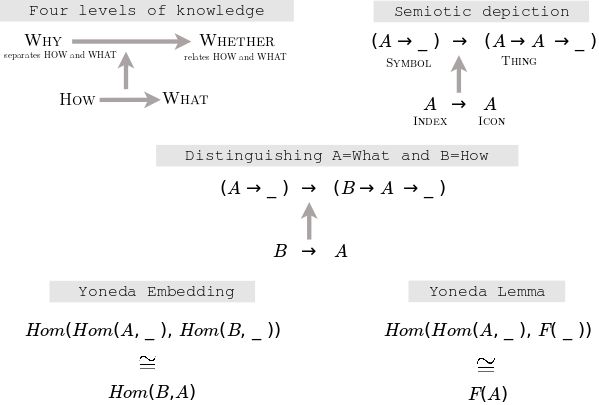
Knowing is understanding scope. Knowing is conditional understanding which varies in scope. The four levels of knowledge are four levels of separating scope, which is to say, understanding scope.

• Why separates everything - it is the brake holding back How.
• How separates anything - it is the functor that maps the object to its relationships.
• What separates something - it is a particular object distinct from and in the context of its relationships.
• Whether separates nothing - it is the state where there is no more separation, there is only relation.

Natural Isomorphism

Consequences

Example: Preorders

Robert Harper: I find it helpful to consider a degenerate form of the Yoneda Lemma, for pre-orders, in which case it says that {$x\leq y$} iff {$(\forall z)\, z\leq x \Rightarrow z\leq y.$} From left to right use transitivity of the preorder; from right to left, instantiate z to x, and use reflexivity. The full form of the Lemma is a generalization of this simple, but surprisingly useful, observation.

{$A\leq B$} iff {$(\forall C)\, C\leq A \Rightarrow C\leq B.$}

Example: Cayley's theorem

The Fundamental Theorem of Computation

• The Yoneda Lemma is the Fundamental Theorem of Computation. It is the mathematical expression of the following basic idea about computation: The validity of a computation is basically the same whether it is a self-standing program or whether it is one step in a larger program.

Automata Hierarchy

• Context free grammars are important for marking block structure in programming, where subroutines begin and end.

{$\frac{1}{r^2}$} laws

The {$\frac{1}{r^2}$} laws are said to arise from

• a conserved quantity (force, energy, etc.) is evenly radiated outward from a point-source in three-dimensional space, thus consider the intensity of radiation through a sphere with surface area {$4\pi r^2$}
• surface area of space (in Einstein's general relativity, per Louis Carroll)
• quantum field theory (see Zee)
• for an irrotational vector space in three-dimensional space, the divergence is zero outside of the source
• see: Inverse-square law

Entropy

• Yoneda law expresses entropy.
• Gibbs and Boltzmann interpretations. Patricia Palacios talk. Gibbs interpretation carves up the domain like Riemannian integration; Boltzmann interpretation carves up the range like Lebesgue integration. Gibbs is human (how, what) and how we think and how our physical quantities that we measure make sense, but Boltzmann is divine (why, whether) and how nature actually is. Relate to the Yoneda lemma.
• Entropy is a function of the state of a system. Change in entropy is determined in terms of the initial and final states. So change in entropy would be modeled by a pushdown automata, a context free language. If a process is reversible, then entropy stays the same, but if a process is irreversible, then entropy increases. So reversibility is crucial here and it relates to whether or not the number of input variables is greater than the number of output variables. A process is irreversible if it is not monic, if two states can lead to the same state.
• The ambiguity in a system can be thought of as the lack of information about a system.
• Fivesome expresses second law of thermodynamics.
• Sixsome expresses moral prerogative to reverse the second law - to create and not destroy.
• Is related to the global quantum - the ability to reconfigure - the existence of subsystems.
• Global quantum is related to coarse graining. Macrostates "look the same" and microstates are complete information.
• Boltzman entropy: Coarse graining is chosen subjectively.
• Related to information - how ambiguous the configurations are.
• We choose what is the observable.
• Gibbs entropy. Low entropy is high information (more spiked distribution) and high entropy is uniformly spread out probability distribution.

Global quantum

Calculate on the basis of the global quantum

• The Hierarchy Problem, the Cosmological Constant, the Vacuum Energy
• Think of the graviton as reversed, from above, thus contradictory, expressing the global quantum. Could that be related to supersymmetry?
• Think of general relativity as describing vibrations = symmetry breakings from above. And as expressing U(0).
• The classical world is in the gap between quantum from above and from below.
• Think of string theory as not refering to particles but to subsystems - vibrations.
• String theory is really a tube theory (the string is a crosssection). So we can think of it as a container for Feynman diagrams, for specific particles. Tube theory comes from above, so it typically organizes huge systems. Particle theory formulates answers but tube theory formulates questions. Measurement imposes tube theory upon particle theory.
• Opens up an algebra of gaps and cracks that descends from the top down rather than from the bottom up.
• This is an environment for number theory, probablity (correlation, and often more importantly, lack of it), statistics (related also to the Pearson family), graph theory (as relates to cliques and such), infinities.
• Conservation laws mediate changes in the constitution of a system in terms of subsystems.
• Yoneda lemma and universality, random matrices - shifting of the structure of a system to subsystems.
• Subsystems "pop out" when they are able to factor out their external relationships and act as a whole.
• Humans can choose to behave spiritually (with regard to a perspective outside the universe) or not. This happens through eternal growth, through appreciating that "God does not have to be good", "life is not fair", and thus living as an individual, ultimately not beholden to this world, one with that beyond it.
• Gravity and {$r^2$} law are consequences of the global quantum, of universality (the shift from quadratic to linear) as per Yoneda's lemma.
• Global quantization forces the system to have defects (in the form of subsystems).
• The deepest value is a fixed point among the gaps and cracks.
• The open evolution of the superposition of the system's various possible constitutions in terms of subsystems is a basis for freedom as to how it is resolved in the future.

Experiment and measurement

An experimental measurement is a very special situation because it is extreme by design. It is connecting the global quantum with the local quantum. Thus it is opening up a world in the classical domain where different resolutions are entertainable.

Building knowledge

Foursome - Yoneda lemma

• You can't accumulate knowledge without suspending the shift from how to what.
• Science is about suspension.
• Divine knowledge must come from human knowledge.
• God's question is thus a human question.
• Science is about the local bundle - acquiring partial knowledge.

Universality

Quanta magazine has published a series of interesting articles about the https://www.quantamagazine.org/search?q[s]=universality | universality principle in statistics, and also the Tracy-Widom distribution including this short video. I happened to learn about this just after my interpretation of the Yoneda lemma. I will explain the possible link that I perceive between the two.

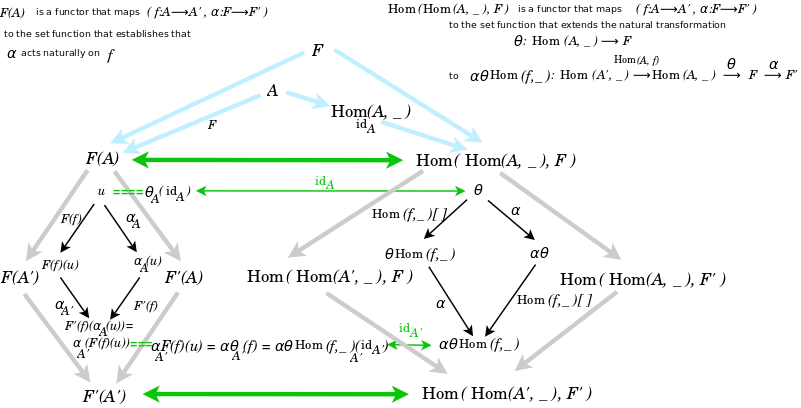
The Yoneda Lemma establishes a natural isomorphism which says that we can look at functors from a category (C) to (Set)

in two different ways. In my understanding, on the one hand, we can think of them as a calculation taking place in its own system, in which case we just look at the network of morphisms. On the other hand, we can think of them as a calculation taking place within a subsystem of a larger system, in which case we need to have initial states and final states, which is to say, we need to have objects.

What is the value of having two points of view when they are naturally isomorphic? Well, apparently, those different points of view can matter, as follows. From the network of morphisms point of view, the network grows as (n2), whereas from the systems and subsystems of objects point of view, the network grows as (n). Simply put, the number of possible binary relationships is quadratic to the number of states or nodes or objects. So as a system grows, it can be burdensome to maintain the quadratic growth, and if at all possible, one might shift perspectives to express the same system in terms of linear growth. Which is to say, if we have a cost to our perspectives, then we may shift them, yielding a phase transition. This is to say that the two points of view may have real implications. In other words, they may be real. Of course, cognitively, they are real, but they may be real not just cognitively. That makes our thinking about these things all the more interesting.

It seems possible that the Tracy-Widom distribution models precisely such a shift. On the one side it goes down (e−N) and on the other side it goes down (e−N2), and apparently it models this phase transition.

The asymmetry of the statistical curve reflects the nature of the two phases. Because of mutual interactions between the components, the energy of the system in the strong-coupling phase on the left is proportional to ( N^2 ). Meanwhile, in the weak-coupling phase on the right, the energy depends only on the number of individual components, ( N ). “Whenever you have a strongly coupled phase and a weakly coupled phase, Tracy-Widom is the connecting crossover function between the two phases,” Majumdar said. At the Far Ends of a New Universal Law

Furthermore, the identity morphisms in the Yoneda Lemma could be crucial for such transitions. Imagine a system that is a collection of interrelated actions (arrows) which satisfy a composition law, but without any objects. And imagine that the system keeps growing through the addition of new actions. The burden of keeping track of everything will grow. Now some of those actions may self-compose, which is to say, they may loop upon themselves. And some of those self-looping actions may have no effect on any other actions, upon composition, which is to say, they are identity actions, "do nothing" actions. Then what could happen is that those identity actions could anchor and define a subsystem. What does such a definition mean? It means that a phase transition takes place, where many of those identity actions, and all the related actions, may form a coherent subsystem, disjoint from the main system, that can "drop out" of it. And their dropping out is simply a matter of a shift in perspective. They can still be thought of as in the main system, but they can also be thought of as a self-standing subsystem which is incorporated into the main system, and they can also be thought of as their very own system. The Yoneda Lemma, in my interpretation, is the framework that allows for these shifts and ambiguities in perspective.

Which is to say, the Yoneda Lemma may be precisely the conceptual framework that grounds such a shift in perspective by which a growing system comes to be made up of subsystems.

As I read a bit about random matrices, which is related to this, I saw that such concepts are important in the study of topological insulators. There is a nice series of videos and lecture notes on that, Course on topology in condensed matter. I learned that "zero energy excitations" are crucial in this subject. When there are no such zero energy excitations, then certain systems aren't able to transform into other systems, and thus we get classes of systems. Well, not knowing anything, such "zero energy excitations" bring to mind the "do nothing" actions.

Another physical idea in all of this is that objects and arrows are distinguished in the way that fermions and bosons are. Two objects cannot be in the same place, and the same is true for fermions. But two arrows can be in the same place, and the same is true for bosons. I mean to say that two arrows can start at the same object and end at the same object but be entirely different arrows. So a shift from an "object point of view" to an "arrow point of view" may be like a shift from "fermion statistics" to "boson statistics".

These mathematical connections are very interesting to me because the topological insulators are classified by Bott periodicity, which I think is related to an eight-cycle of conceptual frameworks (divisions of everything) that is central in my philosophy. Also, they relate to Dysons's Threefold Way, symmetry classes of random matrices (complex Hermitian, real symmetric, or quaternion self-dual) that I think relate to the classical Lie groups, which I think are related to the cognitive frameworks that I study, including the foursome: Whether-What-How-Why.

I think the Yoneda Lemma is modeling the relationship between a system and a subsystem. That is an asymmetric relationship and so it involves an asymmetric phase transition. From my studies of the ways of figuring things out in math and physics, there is what happens before we have a system, and what happens once we have a system. And at the crucial point in between, we have in physics the establishment of a subsystem within a system (as with Faraday's pail). And in math, we have a symmetry group. Well, the Yoneda Lemma is a generalization of Cayley's theorem, whereby every group can be thought of as a permutation group. And here we see the alternatives - we can keep track of a group using (n×n) matrices, or we can allow it to keep track of itself, however it likes, using its own (n) elements.

The Tracy-Widom distribution deals with the largest eigenvalue for a random matrix. The universality principle is an apparently related but slightly different matter of the spacing between all of the eigenvalues. I just want to add that such a spacing also seems like a very important matter in emerging systems. In our universe, it is surprising and very important for physicists that the forces in nature have their effects at different orders of magnitude, because otherwise it would be impossible for us to tease them apart and make sense of any of it. Similarly, architect Christopher Alexander, in his 15 principles of life, notes the importance of Levels of Scale, typically of size 3, which are crucial so that we have gaps between the levels. Apparently, these could be mechanisms for assuring such gaps in levels of scale.

I want to conclude with the following idea from Silicon Valley on the value of networks. A single fax machine is worthless. It becomes valuable when there is a second fax machine. And with each new fax machine, the value of the network grows by that machine's possible relations with all the other machines. Which is to say, the value of the network grows quadratically. Of course, the flipside is that the cost of a network can grow quadratically, and that can drive the appearance of subsystems within the system.

Learning from Videos

Bartosz video

• You can take the logarithm of an exponential, of a hom functor, of a representable functor, of a product type but not a sum type.
• From a representable functor you can get to any other functor using a natural transformation. (One-way). If both ways, then that functor is a representable functor.
• Hom functor from C to Set.
• Category Set mixes levels of abstractions and we can compare them.

Proof of Yoneda lemma

• You have to specify where you will send the identity map - you have to make a definite choice - as with the Axiom of Choice - so this is where choice (probability) comes into the foursome - so there should be four ways of looking at this choice