- MathNotebook
- MathConcepts
- StudyMath
- Geometry
- Logic
- Bott periodicity
- CategoryTheory
- FieldWithOneElement
- MathDiscovery
- Math Connections
Epistemology
- m a t h 4 w i s d o m - g m a i l
- +370 607 27 665
- My work is in the Public Domain for all to share freely.
- 读物 书 影片 维基百科
Introduction E9F5FC
Questions FFFFC0
Software
Adjunction, Classify adjunctions, Adjunction in statistics, Category theory, Limits vs colimits, Equivalence, Sameness
Understand why there are three definitions of adjunction.
伴隨函子的定义
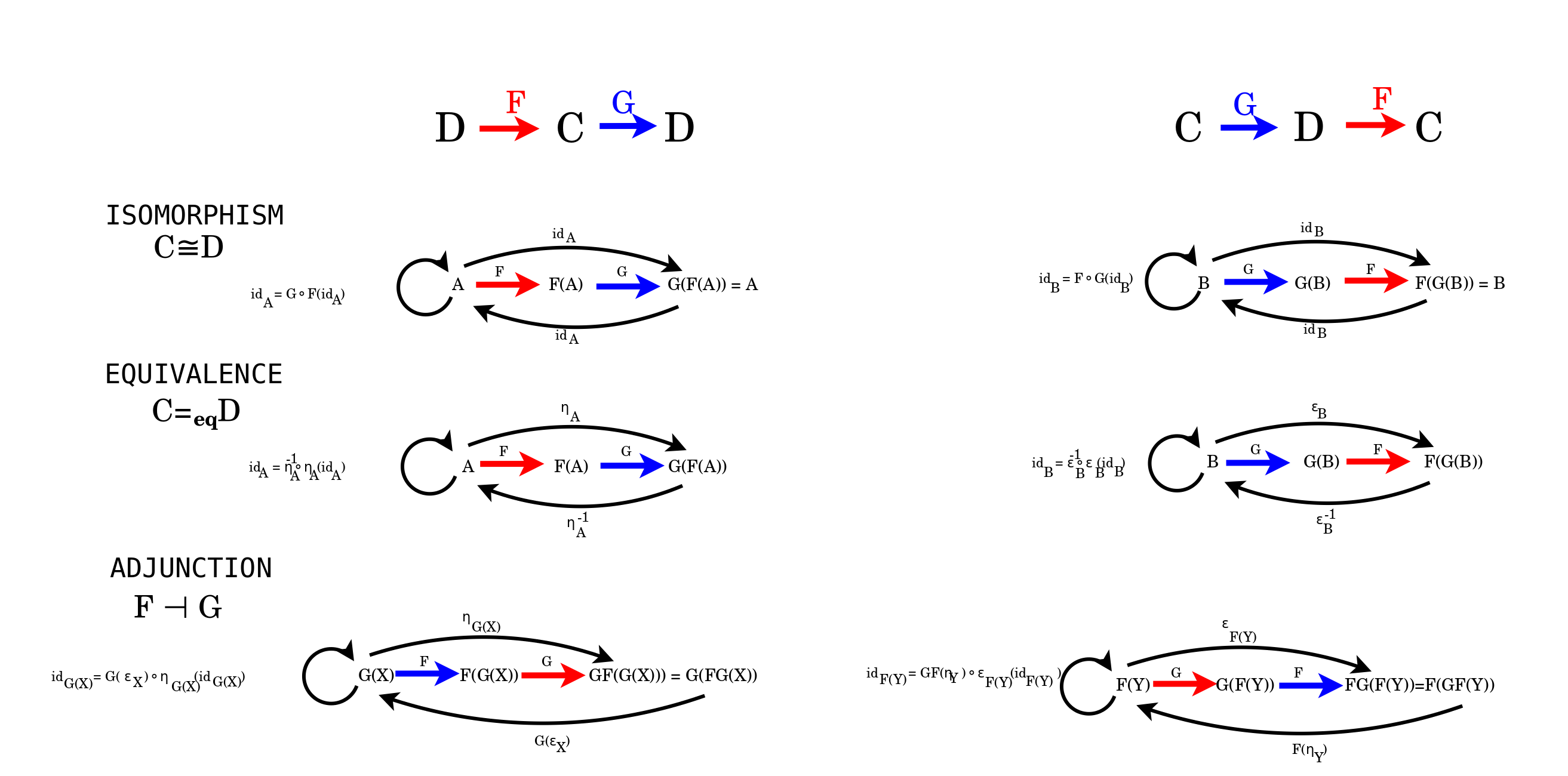
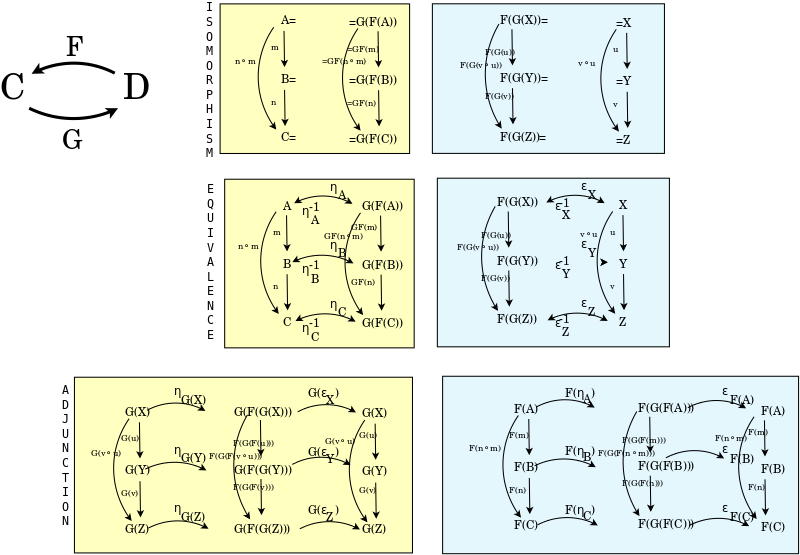
Isomorphism, equivalence, adjunction
- Correct and improve my diagram relating the definitions of isomorphism, equivalence and adjunction.
- Equivalence depends on 2 conditions. Does adjunction depend on 3 conditions? Isomorphism on 1 condition? Identity on O conditions?
Understand the three ways of thinking about (and defining) adjunction.
- Explain why there are three or more definitions of adjunction.
- How are the three ways of defining adjunctions interrelated? Is that exhaustive?
- Consider if there are four definitions which together express the formula for perspective (požiūrio lygtis)
- Understand which definition is most closely related to the Yoneda lemma and what do the other definitions say about the Yoneda lemma.
- Are the three ways of thinking about adjunction related to the Curry-Howard-Lambek correspondence?
- Think of definitions of adjunctions as ratios of differences. Compare this with {$SU(2)$} and with cross-ratios.
- How is the Lawvere definition related to the universal mapping property definition?
Understand the universal mapping property.
- What is the role of comma categories and the universal mapping property in adjunctions?
- Universal mapping property: What is the intuitive difference between a universal pair (with clashing arrows {$\rightarrow \leftarrow$}) and a couniversal pair (with compatible arrows {$\leftarrow \leftarrow $})?
- Rethink adjunction in terms of a unique morphism for all - exists - for all - exists.
- Can the definition of adjunction in terms of the universal mapping property be restated in terms of terminal objects (and the functor FG) rather than initial objects (and the functor GF)?
- Correct and improve my template for understanding adjunction in terms of the universal mapping property.
- Use the adjunction template to write out the logic by which functors have or have not adjoint functors.
- Analyze adjunctions like Awodey (videos) in terms of universal property constructions.
Understand how the various definitions of adjunction are related
- Understand how to go from one definiton of adjunction to another and gain intuition on what this means in practice for various examples.
- Check: the universal mapping property relates triangle identity to the identity.
Why there are various definitions of adjunction
Defining adjunction depends on strings of eight objects and seven morphisms. This is to show that associativity of the composition morphisms holds in the category and to show that functors respect composition.
The four definitions of adjunction arise from the order in which we describe the bijection, the functoriality of F and G, and the natural isomorphism.
- HomSet definition. Describe bijection first. In parallel, describe the functoriality of F and G. Then combine by extending the bijection as a natural isomorphism.
- Universal mapping property with regard to the functor F (alternatively, the functor G). Establish the functoriality of F. Then define G as a map by describing the desired bijection and natural isomorphism. Then demonstrate that G is a functor.
- Triangle identities. Given two functors. Define unit and counit as natural isomorphisms. Then describe the bijection by way of the triangle identities.
- Representing objects definition. nLab: representing objects. Descrbe the functor F. Then define G as a map that output representing objects. Then show that there is a natural isomorphism between the relevant homsets. And then the isomorphism yields for each object in C a bijection such that a diagram commutes with regard to c, fixing d. This asserts naturality in the first variable, which then implies naturality in the second variable.
There are four kinds of definitions for adjunction. This describes the formula for a perspective:
- Homset - balanced
- UMP for counit - step in ?
- UMP for unit - step out ?
- Triangle identities - consciousness
The triangle identities have the virtue of being entirely “algebraic” — no quantifiers, limits, Hom-sets, infinite conditions, etc. Thus anything defined by adjoints, such as free groups, product spaces, quantifiers, . . . can be defined equationally. This is not only a matter of conceptual simplification; it also has important consequences for the existence and properties of the structures that are so determined. (Awodey, 10.1)
What are the definitions of adjunction
Homset definition
Homset
- HomSet: The parenthesis establishes three zones: inside, border, outside, and likewise: outside, border, inside, and the transpose operation.
- HomSet {$\frac{A-B}{A'-B'}$}
Universal mapping definition
A functor {$F:D\to C$} is a left adjoint functor if for each object {$X$} in {$C$} there exists a universal morphism from {$F$} to {$X$}. For each object {$X$} in {$C$} there exists an object {$G(X)$} in {$D$} and a morphism {$ϵ_X: F(G(X))→X$} such that for every object {$Y$} in {$D$} and every morphism {$f: F(Y)→X$} there exists a unique morphism {$g:Y→G(X)$} with {$ϵ_X ∘ F(g) = f$}.
A functor {$G:C → D$} is a right adjoint functor if for each object {$Y$} in {$D$}, there exists a universal morphism from {$Y$} to {$G$}. Spelled out, this means that for each object {$Y$} in {$D$}, there exists an object {$F(Y)$} in {$C$} and a morphism {$η_Y:Y → G(F(Y))$} such that for every object {$X$} in {$C$} and every morphism {$g:Y→G(X)$} there exists a unique morphism {$f:F(Y)→X$} with {$G(f)∘η_Y = g$}.
- Universal mapping property: Can always create a left parenthesis in the first morphism, as close to the object as you like.
- The Universal mapping property shows the asymmetry of F and G which is based on the asymmetry inherent in composition, which is unidirectional, rooted in an object. F and eta is covariant with composition, and G and epsilon is contravariant with composition.
- Universal mapping property {$\frac{A-B}{A-F(A)}$}
- An object in a comma category consists of an analogue and a correction. An object {$Y$} in {$\mathbf{C}$} has an analogue {$G(Y)$} in {$\mathbf{D}$} and an approximation {$F\circ G(Y)$} in {$\mathbf{C}$}. The correction {$\epsilon_Y:F\circ G(Y)\rightarrow Y$} corrects the approximation to yield the object. The correction {$\epsilon :F\circ G\rightarrow I_C$} is a natural transformation from the approximation functor to the identity functor.
Lawvere definition
 Comma category Adjunctions
Comma category Adjunctions- Lawvere showed that the functors {$F:{\mathcal {C}}\rightarrow {\mathcal {D}}$} and {$G:{\mathcal {D}}\rightarrow {\mathcal {C}}$} are adjoint if and only if the comma categories {$(F\downarrow id_{\mathcal {D}})$} and {$(id_{\mathcal {C}}\downarrow G)$}, with {$id_{\mathcal {D}}$} and {$id_{\mathcal {C}}$} the identity functors on {${\mathcal {D}}$} and {${\mathcal {C}}$} respectively, are isomorphic, and equivalent elements in the comma category can be projected onto the same element of {$ {\mathcal {C}}\times {\mathcal {D}}$}. This allows adjunctions to be described without involving sets, and was in fact the original motivation for introducing comma categories.
- Relate to the definition of adjunctions in terms of the universal mapping property.
- The HomSet definition of adjunction depends on sets. This gives an alternative definition that does not depend on sets.
Triangle identity (unit-counit) definition
- Triangle identity: Can cancel left and right parentheses if there is nothing between them. And can create a pair in empty space.
- The triangle identity just prepends eta_A and ignores postpending. Which is to say, we can postpend any G(B). Then it serves to remove the G from the B, and thus reverse the functor.
- The triangle identity definition has the virtue of being entirely equational (Awodey, Chapter 10).
- Unit-counit triangle inequality {$\frac{A-F(A)}{G(F(A))-F(A)}$} and natural transformation {$\frac{A-B}{A-F(A)}$}.
- Unit-counit equations relate postcomposition and precomposition as with pushdown automata and the Yoneda lemma.
- Unit-counit adjunction defines the bar operation so as to define a triangle based on all three relevant dimensions.

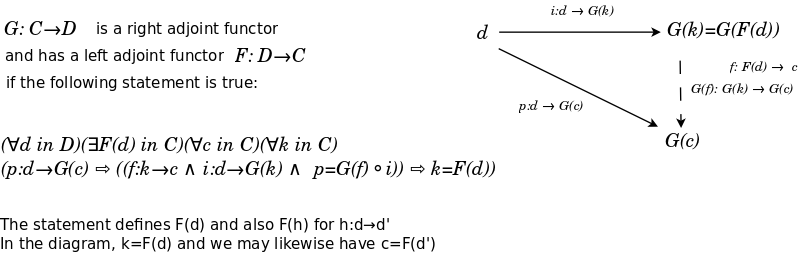
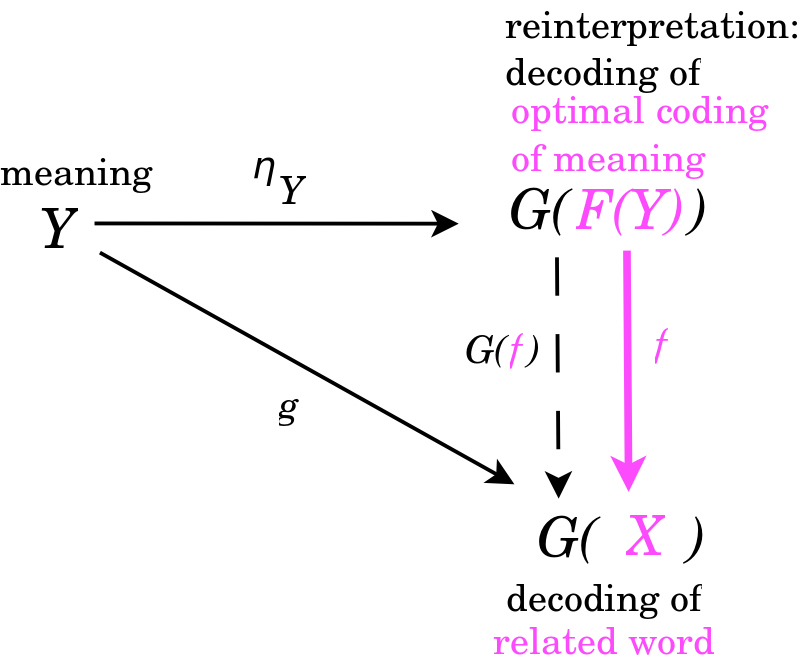
How the definitions of adjunction are related

Compare Isomorphism, Equivalence, Adjunction