Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

克利福德代数

读物

• Pete L. Clark. Quadratic Forms Chapter I: Witt's Theory Study of related orthogonal groups.
• Hovhannes M. Khudaverdian. On relation between quadratic and bilinear form
• Bilinear and quadratic forms
• https://en.wikipedia.org/wiki/Quadratic_form Classification of quadratic forms - Sylvester's signature - number of 0, 1, -1 - classification of real Clifford algebras
• Real quadratic forms
• Quadratic form is one matrix multiplied by another matrix. Or better yet it is summing over all the entries of the matrix where they are written xi xj instead of Aij.
• Whereas linear form, linear equations are described by a single matrix.
• Quadratic form with terms {$a_{ij}x_{i}x_{j}$} is expressed by an upper triangular matrix and hence, when the coefficients are real, as a symmetric matrix {$x_{T}Ax$}.

Field is nullsome

• Can think of there being a zeroth generator {$e_0$} such that {$e_0^2=1$} but also {$e_0=1$}.
• Each generator {$e_i$} can be thought of as dividing {$e_i^2$}. If the latter is {$1$}, then this is a division of everything. And in the case of {$e_0=1$} this division is trivial and we have the nullsome.

Basis elements are simplexes

• The basis elements of geometric algebras are simplexes.
• That is why the dimension is {$2^{n}$}.
• Each basis element is a "square root" of 1 or 0 or -1 - symbols of everything. And thus is a division into two.

Vertices

• Vertices express noncommutativity: {$e_ie_j=-e_je_i$}.

Center is the scalar

• Center expresses commutativity.

Totality is the pseudoscalar

• Totality expresses conditional commutativity.
• The pseudoscalar {$e_{1}e_{2}\dots e_{n}$} is an important concept for me and also for Clifford algebras.

Sign of term expresses orientation

• The sign should express what it means to add or subtract a term.
• The sign could refer to the creating or dismantling of the simplex; the inside or the outside; the center or the totality/complement.

Coefficients express addition of like terms

• The coefficient of a term should express what it means to add the same terms, and to subtract them and scale them.
• Think of a term as a simplex where the center is the origin from which the vectors go, and which is related to the self-standing scalars.

Squares are redundancies

• The square equals +1, 0 or -1.
• Think of the product {$e_ie_j=-e_je_i$} as an angle between e_i and e_j. Reordering the generators gives us the negative angle. If the vectors point in the same direction, then we can have {$e_ie_i=0$}. Or we can interpret one of them as going (say) clockwise all around the circle with regard to the previous one, so that the angle between them is {$e_ie_i=1$}, or possibly counterclockwise, yielding {$e_ie_i=-1$}. And yet {$(-1)^2=1$} so what would that mean?
• The square is the path from a vertex to itself.
• The interpretation of the square depends on the interpretation of the vertex with regard to the space. If the vertex is included in the space, then squaring it means that we have two dimensions that are the same, degenerate, and so the value is zero and the volume is zero. If the squared vertex gets removed, then if it retains the orientation (as if the needle was pulled out backwards) then we have the value as before, and if it switches orientation (as if the needle was turned around in pulling it out) then we get negative of the value.
• This loop removes the vertex and at the same time can A) keep the rest of the simplex (adjusting the edge) - letting go of the slack, B) demolish the entire simplex - by cutting it, C) or it flips the perspective on the simplex - reorienting the slack.
• Clifford algebras may be thought of as quantizations (cf. quantum group) of the exterior algebra, in the same way that the Weyl algebra is a quantization of the symmetric algebra.

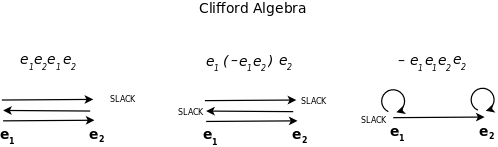
Terms are paths on simplexes

• Each terms is a simplex with the vertices ordered in a certain way.
• Thus a term may be identified with a path on a simplex that visits all of its vertices.
• A positive or negative term may be interpreted as a path for which the slack is at the end (in the positive case, infinitely increasing slack) or at the beginning (in the negative case, finite, decreasing slack).
• The slack determines the direction we associate to the path. Reversing the order of a segment switches this direction, the parity, the sign, the location and nature of the slack.
• Parentheses define slack - which is directed. And the negative signs indicate the direction.
• Slack is always directed because one end is the "center" and the other is the "void". The two directions distinguish unbounded, increasing slack, and bounded, decreasing slack.

Even subalgebra of Clifford algebra.

• The even subalgebra is generated by the edges.
• The complex numbers are generated by {$i=e_{1}e_{2}$}.
• Identify complexes with a line-segment 1-simplex; and with a point 0-simplex.
• The quaternions are generated by {$i=e_{1}e_{2}, j=e_{3}e_{1}, k=e_{2}e_{3}$}.
• Identify quaternions with a triangle 2-simplex; and with a line segment 1-simplex.
• Clifford algebra. Think of it as Field + Simplex where the extra Field dimension can be interpreted in four different ways to get the choice frameworks. For example, it can be "nonexistence of a vertex", or it can be an additional vertex e0.
• Clifford algebra has a global (zeroth) dimension-direction, a zeroth generator, given by the field R. It is the non-choosing of a vertex, as with simplexes.

Compare choice frameworks and the center of a Clifford algebra (where the pseudoscalar is the totality)

• simplex - center & totality - Clifford algebra
• crosspolytope - center, no totality - Clifford algebra
• cube - no center, totality - real form?
• coordinate systems - no center, no totality - real form?

In the Clifford algebra intepretation, the operation +1 adds a vertex (and the identity), +2 adds two vertices (and the identity and an edge), +3 adds three vertices (and the identity and three edges and one face).

Ideas

• Relate {$F_1$} with the basis element 1 in a Clifford algebra.
• R+R expresses the nullsome, the combination of the mind that knows and the mind that does not know, all is good and all is bad, leading to a collapse, a contradiction. H+H expresses the foursome, the independence of knowledge from us.
• Divisions of everything should have perspectives that are given by chains but they should also be built up out of pairs where you originally have a 1 plus a perspective and furthermore you have genealogy where you can get chains of having stepped in, stepped out and so on.
• If you have a perspective, let's say you are stepping into it and then you step into that, then the idea may be that you have stepped out. Actually, I have it backwards. When you step out, that is when the perspective is written down. If you are stepped in, then there is no stepped out. But if you step out of the same perspective twice, then that's the same as stepping into it.
• If you step out of a perspective and you step out of that same perspective with that same perspective, if the same perspective steps out of itself, then that's the same as stepping in, then why would that be 1 or -1? and I think that's the difference between God's perspective and a human perspective.
• {$+1$} perspective {$e_i$} Is this a person's perspective upon themselves? {$e_i^2=-1$}. {$+2$} perspective on a perspective, why is {$e_ie_j=-e_je_i$}? {$+3$} perspective on perspective on perspective
• Divisions of everything are given by the number of generators. {$e_1$} is {$1$}, {$e_1e_2$} is {$2$}. {$M_2(\mathbb{H})$} is the foursome.
• {$-1$} means flip orientation and {$1$} means don't.
• Generators {$R=e_i^2$} definie inner structure whereas matrices {$M_n()$} define external relationships, different perspectives for the same relationships.
• Real numbers = slack, Complex numbers = null, Quaternions = perspective

Starting point

• God does not distinguish between the nullsome and the onesome so for God they come together as {$C$}.

Intuitions

• Start from C - as the basic duality - and end up at C inverted (perhaps the conjugate) and go back. This circle is used to list the quotients of Clifford modules {$GL_{n}(\mathbb{R})/GL_{n}(\mathbb{C})$} check? etc If you multiply all the quotients together than you get the identity (?)

• The two-cycle is: the undefined (the nullsome) yields the defined (the foursome), which yields the defined undefined (the eightsome), which is the same as the undefined (the nullsome).
• Complex case: 2-periodicity - divisions having 4 (nežinojimas) or 2 (žinojimas) representations. Real case: 8-peridocity.
• Clifford algebras. Complex numbers unite divine existence. Real numbers distinguish human knowledge.

Facts

• In the complex case, there is only one nondegenerate quadratic form, for which all of the coefficients are 1.
• The Wikipedia article explains that in the complex case the quadratic form there is no signature because {$+1 = i^2(–1)$}. Whereas in the real case the signature distinguishes between the number of {$+1$} and the number of {$–1$}.
• For complex numbers there is essentially only one quadratic form {$\sum_{i=1}^{n}u_{i}^2$} because squaring a complex number can generate -1 as needed.
• Periodicity 2 in the complex case.

Here is the reason for twofold periodicity.

• The totality (the pseudoscalar) commutes with every element precisely when n is odd. That is because to move the element from the right hand side to the left hand side we need to swap with n-1 different elements (switching sign) and 1 element which is the same (thus not switching sign).
• {$e_{1}e_{2}\dots e_{n}\cdot e_{i}=(-1)^{n-1}e_{i}\cdot e_{1}e_{2}\dots e_{n}$}
• Thus the pseudoscalar is in the center of the Clifford algebra when n is odd but not when n is even. The center is the subring of elements that commute with all of the elements in the ring. The center of an algebra contains its field.
• Another reason for twofold periodicity is in terms of how the spheres grow. An axis is extended through either side of a circle, yielding two extremes, as with the suspension functor or with the axis of a crosspolytope such as an octogon. Then that axis is rotated around twice, in either direction, to create a new circle, uniting the extremes.
• This is the suspension of a topological space.
• For example, we can imagine the 3-sphere by considering the two hemispheres of a 2-sphere, along with the circle in between them, and imagine them all rotating all of the way around. We have the fourth dimension t=0 at the beginning, at first coinciding of the circle with itself, and at the final coinciding. We have t=1 at the two points in between, thus defining the two extremes, which are positive t=1 and negative t=-1. And as we rotate the 2-sphere, its radius gets smaller, vanishing when t=1 or t=-1, but then reappearing. The fourth dimension gives your distance above the point on the sphere which gives the other three dimensions.
• The 0-sphere is a tiny loop around the 1-dimensional axis.
• Suspension is separation as with space (per the fivesome). Rotation is unification as with time (per the fivesome).
• This relates discreteness (spheres generated by an odd-number of parameters) and continuity (spheres generated by an even-number of parameters).
• The twofold periodicity also relates, in an alternating way, volumes of n-spheres, and surface areas of n-spheres.

Ideas

• In the complex Clifford algebras, Bott periodicity works like a counting process, extending the (dual) chain, interpersed by having two distinct chains (forward and backwards).

I need to understand a real Clifford algebra in the following three ways:

• It is determined by its generators, where {$m$} generators {$\epsilon_1,\dots,\epsilon_m$} square to {$+1$}, and {$n$} generators {$e_1,\dots,e_n$} square to {$-1$}.
• It is expressed in terms of a matrix algebra over {$\mathbb{R}$}.
• It is expressed in terms of {$\mathbb{R}$}, {$\mathbb{C}$}, {$\mathbb{H}$} or matrices with such entries.

I need to be able to go back and forth between these three ways and explain how they are built up and related.

I need to be able to look at these representations and understand which ones are {$\mathbb{Z}_2$}-graded and what that means.

The Clifford algebras are given by their generators, how many square to {$+1$} and how many square to {$-1$}. Then we can have products of generators where they occur no more than once. This yields {$2^n$} possible terms where {$n$} is the total number of generators. Thus we have {$2^n$} basis elements.

读物

• Fuzhen Zhang. Quaternions and Matrices of Quaternions.
• Representation of Lorentz Group and Clifford algebra-I
• Andrzej Trautman. Clifford Algebras and Their Representations.
• Peter Woit. Quantum Theory, Groups and Representations.
• Peter Woit. Topics in Representation Theory: Clifford Algebras. Peter Woit author of Not Even Wrong
• Calvin McPhail-Snyder. Representations of Clifford Algebras.
• Hile, Lounesto. Matrix Representations of Clifford Algebras.
• Yingqiu Gu School of Mathematical Science, Fudan University, Shanghai. Many creative ideas!
  • Ying-Qiu Gu. A Note on the Representation of Clifford Algebra.
• Ying Qiu Gu. Representations of Clifford Algebra. Δ

The way to get a matrix representation is simply to write out a generic element of the Clifford algebra, for example, {$a + b\epsilon_1 + ce_1 + d\epsilon_1e_1$} and consider what happens when we multiply on the left by a basis element. If we write out the basis in a particular order, then we get a related matrix representation.

What ordering to use? Here are some principles that come to mind.

• Group the terms according to their highest generator. This allows us to see how the previous representations are embedded in the later ones.
• Order terms according to the number of generators in the term. This allows us to see related symmetries.

{$Cl_{0,0}=\mathbb{R}$}

{$Cl_{0,1}$} has elements of the form {$a + be_1$}. Note that {$e_1(a + be_1) = -b + ae_1$}. Thus the matrix representation is:

{$I = \begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix}$}

{$e_1 = i = \begin{pmatrix}0 & -1 \\ 1 & 0\end{pmatrix}$}

By inspection, we have {$\mathbb{C}$}.

{$Cl_{1,0}$} has elements of the form {$a + b\epsilon_1$} where {$\epsilon_1^2=+1$}. These are the split-complex numbers.

Note that {$\epsilon_1(a + b\epsilon_1) = b + a\epsilon_1$}. Thus the matrix representation is:

{$I = \begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix}$}

{$\epsilon_1 = \epsilon = \begin{pmatrix}0 & 1 \\ 1 & 0\end{pmatrix}$}

This is isomorphic to {$\mathbb{R}\oplus\mathbb{R}$}. Note from Direct sum of modules that a direct sum of algebras, such as {$\mathbb{R}\oplus\mathbb{R}$}, has product defined by {$(x_1+y_1)(x_2+y_2)=(x_1x_2+y_1y_2)$}, which means such a direct sum is actually, a categorical product, a product in the sense of category theory.

The isomorphism is given by...

Math Stack Exchange: Simple {$M_n(D)$}-module with {$D$} a division ring The third answer calculates explicitly and shows that any simple module of {$M_n(D)$} is isomorphic to a column in the matrix. This means that there is only one kind of simple module. What confuses me is that this particular module can be talked about in various ways. And each of the columns yields such a module. But the crucial point is that they all are isomorphic, and in that sense, there is only one simple module.

Husemoller, Proposition 6.4, page 162, explains that there are two irreducible modules over {$F(n)\oplus F(n)$}. They are given by the two projections {$F(n)\oplus F(n)\rightarrow F(n)$} followed by the action of {$F(n)$} on {$F^n$}. Both of these representations have dimension {$n$} over {$F$}.

Note that this has two irreducible representations, namely {$(a,b)\rightarrow (a)$} and {$(a,b)\rightarrow (b)$}.

Note that it sends

{$1=(1,1)\rightarrow\begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix}$}

{$e_1=(1,-1)\rightarrow\begin{pmatrix}1 & 0 \\ 0 & -1\end{pmatrix}$}

This means that we have one irreducible trivial representation that sends {$1\rightarrow (1)$} and {$e_1\rightarrow (1)$}, and another irreducible alternating representation that sends {$1\rightarrow (1)$} and {$e_1\rightarrow (-1)$}.

And similarly, using block matrices, for {$\mathbb{C}\oplus\mathbb{C}$} and {$\mathbb{H}\oplus\mathbb{H}$}.

{$\mathcal{Cl}(2,0)\cong M_2(\mathbb{R})$} {$1\leftrightarrow\begin{pmatrix}1 & 0\\0 & 1\end{pmatrix}, e_1\leftrightarrow\begin{pmatrix}1 & 0\\0 & -1\end{pmatrix}, e_2\leftrightarrow\begin{pmatrix}0 & 1\\1 & 0\end{pmatrix}, e_1e_2\leftrightarrow\begin{pmatrix}0 & 1\\-1 & 0\end{pmatrix} $} Note the choice of generators yields {$e_1^2=1$}, {$e_2^2=1$}, {$(e_1e_2)^2=-1$}.

{$\mathcal{Cl}(1,1)\cong M_2(\mathbb{R})$} {$1\leftrightarrow\begin{pmatrix}1 & 0\\0 & 1\end{pmatrix}, e_1\leftrightarrow\begin{pmatrix}1 & 0\\0 & -1\end{pmatrix}, e_2\leftrightarrow\begin{pmatrix}0 & 1\\-1 & 0\end{pmatrix}, e_1e_2\leftrightarrow\begin{pmatrix}0 & 1\\1 & 0\end{pmatrix} $} Note the choice of generators yields {$e_1^2=1$}, {$e_2^2=-1$}, {$(e_1e_2)^2=1$}.

{$\mathcal{Cl}(1,0)\cong\mathbb{R}\oplus\mathbb{R}$} {$1\leftrightarrow (1,1), e_1\leftrightarrow (1,-1), \frac{1+e_1}{2}\leftrightarrow (1,0), \frac{1-e_1}{2}\leftrightarrow (0,1)$}

{$\mathcal{Cl}(0,0)\cong\mathbb{R}$} Real numbers {$1\leftrightarrow 1$}

{$\mathcal{Cl}(0,1)\cong\mathbb{C}$} Complex numbers {$1\leftrightarrow 1, e_1\leftrightarrow i$}

{$\mathcal{Cl}(0,2)\cong\mathbb{H}$} Quaternions {$1\leftrightarrow 1, e_1\leftrightarrow i, e_2\leftrightarrow j, e_1e_2\leftrightarrow k$}

{$\mathcal{Cl}(0,3)\cong\mathbb{H}\oplus\mathbb{H}$} Split-biquaternions

{$1\leftrightarrow 1, e_1\leftrightarrow i, e_2\leftrightarrow j, e_3\leftrightarrow \varepsilon k , e_1e_2\leftrightarrow k, e_2e_3 \leftrightarrow \varepsilon i , e_3e_1 \leftrightarrow \varepsilon j , e_3e_2e_1 \leftrightarrow \varepsilon $}

{$(1,1)\leftrightarrow \frac{1+e_3e_2e_1}{2}, (i,i)\leftrightarrow \frac{e_1+e_3e_2}{2}, (j,j)\leftrightarrow \frac{e_2+e_3e_1}{2}, (k,k)\leftrightarrow \frac{e_1e_2+e_3}{2}, (1,-1)\leftrightarrow \frac{1+e_1e_2e_3}{2}, (i,-i)\leftrightarrow \frac{e_1+e_2e_3}{2}, (j,-j)\leftrightarrow \frac{e_2+e_1e_3}{2}, (k,-k)\leftrightarrow \frac{e_1e_2-e_3}{2} $}

The most clear and helpful exposition is Theorem 5.6 in Dale Husemoller's Fibre Bundle.

José Figueroa-O'Farrill. Spin Geometry

• Lecture 1: Clifford algebras: basic notions
• Lecture 2: Clifford algebras: the classification This gives recursion formulas for constructing the Clifford algebras. But I found it confusing and the Husemoller exposition is much more clear.

Recursion formulas

• {$\mathcal{Cl}(0,n+2)\cong \mathcal{Cl}(n,0) \otimes \mathbb{H} \cong \mathcal{Cl}(n,0) \otimes \mathcal{Cl}(0,2)$}
• {$\mathcal{Cl}(n+2,0)\cong \mathcal{Cl}(0,n) \otimes \mathbf{M}_2(\mathbb{R}) \cong \mathcal{Cl}(0,n) \otimes \mathcal{Cl}(2,0)$}
• {$\mathcal{Cl}(s+1,t+1)\cong \mathcal{Cl}(s,t) \otimes \mathbf{M}_2(\mathbb{R}) \cong \mathcal{Cl}(s,t) \otimes \mathcal{Cl}(1,1)$}

{$\mathbb{R}$}	{$\mathbb{C}$}	{$\mathbb{H}$}	{$(\mathbb{R}\oplus\mathbb{R})\otimes\mathbb{H}$}	{$\mathbf{M}_2(\mathbb{R})\otimes\mathbb{H}$}
{$\mathbb{R}\oplus\mathbb{R}$}	{$\mathbf{M}_2(\mathbb{R})$}	{$\mathbb{C}\otimes\mathbf{M}_2(\mathbb{R})$}	{$\mathbb{H}\otimes\mathbf{M}_2(\mathbb{R})$}
{$\mathbf{M}_2(\mathbb{R})$}	{$(\mathbb{R}\oplus\mathbb{R})\otimes \mathbf{M}_2(\mathbb{R})$}	{$ \mathbf{M}_2(\mathbb{R})^2$}	{$\mathbb{C}\otimes\mathbf{M}_2(\mathbb{R})^2$}
{$\mathbb{C}\otimes\mathbf{M}_2(\mathbb{R})$}	{$\mathbf{M}_2(\mathbb{R})^2$}	{$ (\mathbb{R}\oplus\mathbb{R})\otimes \mathbf{M}_2(\mathbb{R})^2$}	{$\mathbf{M}_2(\mathbb{R})^3$}
{$\mathbb{H}\otimes\mathbf{M}_2(\mathbb{R})$}	{$\mathbb{C}\otimes\mathbf{M}_2(\mathbb{R})^2$}	{$ \mathbf{M}_2(\mathbb{R})^3$}	{$(\mathbb{R}\oplus\mathbb{R})\otimes\mathbf{M}_2(\mathbb{R})^3$}
{$(\mathbb{R}\oplus\mathbb{R})\otimes\mathbb{H}\otimes\mathbf{M}_2(\mathbb{R})$}	{$\mathbb{H}\otimes\mathbf{M}_2(\mathbb{R})^2$}	{$ \mathbb{C}\otimes\mathbf{M}_2(\mathbb{R})^3$}	{$\mathbf{M}_2(\mathbb{R})^4$}

Intuitions

• The eight-cycle arises from the details: adding four perspectives yields the foursome, the defined. Then we can, dually, think of subtracting perspectives from that. But the subtraction (relaxing, removing perspectives) is defined by adding perspectives, yielding the fivesome which lets a sensor be free in time and space, the sixsome lets the conditional sensor relate to the unconditional, the sevensome lets the external unity (of the whole) match the internal unity (of slack) in a dualistic way, the eightsome has the system collapse.

读物

• https://en.wikipedia.org/wiki/Clifford_algebra#Structure_of_Clifford_algebras
• https://en.wikipedia.org/wiki/Classification_of_Clifford_algebras
• Classification of Clifford algebras
• Dexter Chua. Clifford Algebras and Bott Periodicity.
• D. Lundholm, L. Svensson. Clifford algebra, geometric algebra, and applications, 2009. Includes the classification.
• José Figueroa-O'Farrill. Course on Spin Geometry.
  • José Figueroa-O'Farrill. Lecture 2: Clifford algebras: the classification

Relevant concepts

• https://en.wikipedia.org/wiki/CCR_and_CAR_algebras
• https://en.wikipedia.org/wiki/Superalgebra
• Dual numbers
• Split-complex numbers
• 4 types of complex representations of real Clifford algebras. And the complex representation may or may not be a complexification of a real Clifford algebra, thus we multiply by 2 to get 8 types of real representations.
• Clifford algebra sequence grows by adding -1 norms. Or, in the opposite direction, by adding +1 norms.
• {$M_2(Cl_{p,q}(\mathbb{R}))=Cl_{p+1,q+1}(\mathbb{R})$}
• The Clifford algebra of U + V is isomorphic to the tensor product of the Clifford algebras of U and (−1)dim(U)/2dV, which is the space V with its quadratic form multiplied by (−1)dim(U)/2d.
• The reals discriminate real and imaginary square roots and so they have a signature {$\sum_{i=1}^{p}u_{i}^2 - \sum_{i=1}^{q}u_{i}^2$}.
• In the real case, the quadratic form q can be put into diagonal form so that it has only square terms with coefficients 1,–1 or 0.
• If all of the coefficients are 0 then we have an external algebra or Grassmann algebra. Its product is the wedge product.
• Periodicity 8 in the real case.

Ideas

• Real Clifford algebras are like negative numbers in that they have positive or negative or mixed signature. Whereas complex numbers do not respect any such distinctions. The reals expand the complexes by breaking symmetry.

The pseudoscalar is a totality as in my study of the binomial theorem, interpreting choice frameworks.

Overview

• Does the pseudoscalar commute with everything? (Is the pseudoscalar in the center?) Yes if {$n$} is odd and no if {$n$} is even.
• Is the square of the pseudoscalar {$+1$} or {$-1$} ?
  • If the pseudoscalar is in the center, then the center will be {$\mathbb{R}\oplus\mathbb{R}$} or {$\mathbb{C}$}, respectively.

If {$n$} is even, then the pseudoscalar commutes with everything (the Clifford algebra is central simple), and if {$n$} is odd, then the pseudoscalar does not commute with everything (the Clifford algebra is not central simple). Note that commuting requires {$e_i$} to switch places with {$n$} generators, one of which is itself, yielding a sign {$(-1)^{n-1}$}. Here the squares of the generators are irrelevant.

{$e_i\cdot e_1e_2\cdots e_{n} = (-1)^{n-1}e_1e_2\cdots e_{n}\cdot e_i$}

Thus the pseudoscalar commutes with all generators precisely when {$n$} is odd.

Squaring the pseudoscalar yields a fourfold periodicity.

• {$1\cdot 1=1$}
• {$e_{1}\cdot e_{1}=Q(e_{1})$}
• {$e_{1}e_{2}\cdot e_{1}e_{2}=-Q(e_{1})Q(e_{2})$}
• {$e_{1}e_{2}e_{3}\cdot e_{1}e_{2}e_{3}=-Q(e_{1})Q(e_{2})Q(e_{3})$}
• {$e_{1}e_{2}e_{3}e_{4}\cdot e_{1}e_{2}e_{3}e_{4}=Q(e_{1})Q(e_{2})Q(e_{3})Q(e_{4})$}
• {$e_{1}e_{2}e_{3}e_{4}e_{5}\cdot e_{1}e_{2}e_{3}e_{4}e_{5}=Q(e_{1})Q(e_{2})Q(e_{3})Q(e_{4})Q(e_{5})$}

This is because in the sum 0+1+2+3+4... we start with even and then have

• even + odd = odd
• odd + even = odd
• odd + odd = even
• even + even = even

Where even means "stay the same" and odd means "switch". Note that here the two are dual!

If {$Q(e_i)=+1$} for all {$i$}, then the sequence is {$1,1,–1,–1,1,1,–1,–1\cdots$}.

If {$Q(e_i)=-1$} for all {$i$}, then the sequence is {$1,-1,–1,1,1,-1,–1\cdots$}, thus advanced by one.

If we have {$p$} generators {$e_i$} for which {$Q(e_i)=+1$} and {$q$} generators {$e_j$} for which {$Q(e_j)=-1$}, then the continutation of the former sequence gets multiplied by {$-1$}. We have the following cases:

• 1,1,-1,-1 continues -1,-1,1,1,
• 1,1,–1 continues 1,-1,-1,1
• 1,1 continues 1,1,-1,-1
• 1 continues -1,1,1,-1

But in any event, we have contributions to the overall sign from the shuffling {$(-1)^{\frac{n(n-1)}{2}) and from those {$q$} generators that square to {$-1$}, yielding {$(-1)^q$}. Given {$n=p+q$} consider the signature {$p-q$}. Note that for integers {$p$}, {$q$}, we have that {$p-q$} is even iff {$p+q$} is even. Further note that {$(p+q)(p+q-1)$} is the product of an even number and odd number, thus necessarily even. But when we divide by 2, is it even or odd? Want to show that

{$\omega^2=(-1)^{\frac{n(n-1)}{2}}(-1)^q=(-1)^{\frac{(p-q)(p-q-1)}{2}}=\left\{\begin{matrix} +1 \;\;\; p-q\equiv 0,1\mod 4\\ -1 \;\;\; p-q\equiv 2,3\mod 4 \end{matrix}\right.$}

A central simple algebra over K is a matrix algebra over a (finite-dimensional) division algebra with center K. For example, the central simple algebras over the reals are matrix algebras over either the reals or the quaternions.

• If V has even dimension then
  • {$Cl(V,Q)$} is a central simple algebra over K.
  • the even subalgebra {$Cl^{[0]}(V,Q)$} is a central simple algebra over a quadratic extension of K or a sum of two isomorphic central simple algebras over K.
• If V has odd dimension then
  • {$Cl(V,Q)$} is a central simple algebra over a quadratic extension of K or a sum of two isomorphic central simple algebras over K.
  • the even subalgebra {$Cl^{[0]}(V,Q)$} is a central simple algebra over K.

The structure of Clifford algebras can be worked out:

• Suppose that the vectors space U has even dimension and a non-singular bilinear form with discriminant d, and suppose that V is another vector space with a quadratic form. The Clifford algebra of {$U+V$} is isomorphic to the tensor product of the Clifford algebras of U and (−1)^dim(U)/2dV, which is the space V with its quadratic form multiplied by {$(−1)^{\frac{\textrm{dim(U)}}{2}}d$}. Over the reals, this implies in particular the formulas below which can be used to find the structure of all real Clifford algebras and all complex Clifford algebras. Here {$p$} is the number of elements such that {$e_i^2=1$} and {$q$} the number of elements {$e_i$} such that {$e_i^2=-1$}:
• {$\textrm{Cl}_{p+2,q}(\mathbf{R}) = \mathrm{M}_2(\mathbf{R})\otimes \textrm{Cl}_{q,p}(\mathbf{R}) $}
• {$\textrm{Cl}_{p+1,q+1}(\mathbf{R}) = \mathrm{M}_2(\mathbf{R})\otimes \textrm{Cl}_{p,q}(\mathbf{R}) $}
• {$\textrm{Cl}_{p,q+2}(\mathbf{R}) = \mathbf{H}\otimes \textrm{Cl}_{q,p}(\mathbf{R}) $}

This yields the following sequences:

{$\textrm{Cl}_{0,0}(\mathbf{R})$}	{$=\mathbb{R}$}	{$=\mathbb{R}$}	{$\textrm{Cl}_{0,0}(\mathbf{R})$}	{$=\mathbb{R}$}	{$=\mathbb{R}$}
{$\textrm{Cl}_{0,2}(\mathbf{R})$}	{$\cong\mathbb{H}\otimes\mathbb{R}$}	{$\cong\mathbb{H}$}	{$\textrm{Cl}_{2,0}(\mathbf{R})$}	{$\cong M_2(\mathbb{R})\otimes \mathbb{R}$}	{$\cong M_2(\mathbb{R})$}
{$\textrm{Cl}_{0,4}(\mathbf{R})$}	{$\cong \mathbb{H}\otimes M_2(\mathbb{R})\otimes \mathbb{R}$}	{$\cong M_2(\mathbb{H})$}	{$\textrm{Cl}_{4,0}(\mathbf{R})$}	{$\cong M_2(\mathbb{R})\otimes \mathbb{H} \otimes \mathbb{R}$}	{$\cong M_2(\mathbb{H})$}
{$\textrm{Cl}_{0,6}(\mathbf{R})$}	{$\cong\mathbb{H}\otimes M_2(\mathbb{R})\otimes\mathbb{H}\otimes\mathbb{R}$}	{$\cong M_4(\mathbb{H})$}	{$\textrm{Cl}_{6,0}(\mathbf{R})$}	{$\cong M_2(\mathbb{R})\otimes \mathbb{H} \otimes M_2(\mathbb{R})\otimes \mathbb{R}$}	{$\cong M_8(\mathbb{R})$}
{$\textrm{Cl}_{0,8}(\mathbf{R})$}	{$\cong \mathbb{H}\otimes M_2(\mathbb{R})\otimes\mathbb{H}\otimes M_2(\mathbb{R})\otimes\mathbb{R}$}	{$\cong M_{16}(\mathbb{R})$}	{$\textrm{Cl}_{8,0}(\mathbf{R})$}	{$\cong M_2(\mathbb{R})\otimes \mathbb{H} \otimes M_2(\mathbb{R})\otimes \mathbb{H} \otimes \mathbb{R}$}	{$\cong M_{16}(\mathbb{R})$}

{$\textrm{Cl}_{0,1}(\mathbf{R})$}	{$\cong\mathbb{C}$}	{$\cong\mathbb{C}$}	{$\textrm{Cl}_{1,0}(\mathbf{R})$}	{$\cong\mathbb{R}\oplus\mathbb{R}$}	{$\cong\mathbb{R}\oplus\mathbb{R}$}
{$\textrm{Cl}_{0,3}(\mathbf{R})$}	{$\cong\mathbb{H}\otimes(\mathbb{R}\oplus\mathbb{R})$}	{$\cong\mathbb{H}\oplus\mathbb{H}$}	{$\textrm{Cl}_{3,0}(\mathbf{R})$}	{$\cong M_2(\mathbb{R}) \otimes \mathbb{C}$}	{$\cong M_2(\mathbb{C})$}
{$\textrm{Cl}_{0,5}(\mathbf{R})$}	{$\cong \mathbb{H}\otimes M_2(\mathbb{R})\otimes \mathbb{C}$}	{$\cong M_4(\mathbb{C})$}	{$\textrm{Cl}_{5,0}(\mathbf{R})$}	{$\cong M_2(\mathbb{R})\otimes \mathbb{H}\otimes (\mathbb{R}\oplus\mathbb{R})$}	{$\cong M_2(\mathbb{H})\oplus M_2(\mathbb{H})$}
{$\textrm{Cl}_{0,7}(\mathbf{R})$}	{$\cong \mathbb{H}\otimes M_2(\mathbb{R})\otimes\mathbb{H}\otimes (\mathbb{R}\oplus\mathbb{R})$}	{$\cong M_8(\mathbb{R})\oplus M_8(\mathbb{R})$}	{$\textrm{Cl}_{7,0}(\mathbf{R})$}	{$\cong M_2(\mathbb{R})\otimes\mathbb{H}\otimes M_2(\mathbb{R})\otimes \mathbb{C}$}	{$\cong M_8(\mathbb{C})$}

If both {$p$} and {$q$} are nonzero, then set {$r=\textrm{min}(p,q)$} and tensor {$r$} copies of {$M_2(\mathbb{R})$} to the Clifford algebra {$\textrm{Cl}_{p-r,q-r}(\mathbf{R})$}.

Note: Morita equivalence. The ring of n-by-n matrices with elements in R, denoted Mn(R), is Morita-equivalent to R for any n > 0. Notice that this generalizes the classification of simple artinian rings given by Artin–Wedderburn theory. To see the equivalence, notice that if X is a left R-module then Xn is an Mn(R)-module where the module structure is given by matrix multiplication on the left of column vectors from X. This allows the definition of a functor from the category of left R-modules to the category of left Mn(R)-modules. The inverse functor is defined by realizing that for any Mn(R)-module there is a left R-module X such that the Mn(R)-module is obtained from X as described above.

• Stack Exchange: How to prove that a ring R is Morita equivalent to {$M_n(R)$}?
• Super Brauer group

BW(R) is isomorphic to Z/8Z. The 8 super division algebras are R, R[ε], C[ε], H[δ], H, H[ε], C[δ], R[δ] where δ and ε are odd elements of square –1 and 1, such that conjugation by them on complex numbers is complex conjugation.

• Andrzej Trautman. Clifford Algebras and Their Representations.
• Susumu Okubo. Representations of Clifford Algebras and Its Applications.
• Bilge, Kocak, Uguz. Canonical bases for real representations of Clifford algebras.
• Clifford module
• Atiyah, Bott, Shapiro
• Todd Trimble. The Super Brauer Group and Super Division Algebras.
• Calvin McPhail-Snyder. Representations of Clifford algebras.
• Hile, Lounesto. Matrix Representations of Clifford Algebras
• Woit. Topics in Representation Theory: Clifford Algebras.
• Gamma matrices
• Higher-dimensional gamma matrices

A Clifford module is a representation of a Clifford algebra.

Wedderburn theorem: Let K = R, C or H and consider the ring {$K(N )$} of {$N × N$} matrices as an algebra over R. Then the natural representation {$ρ$} of {$K(N )$} on the vector space {$K^N$} is, up to equivalence, the only irreducible representation of {$K(N )$}. The algebra {$K(N ) ⊕ K(N )$} has exactly two irreducible representations given by {$ρ_1(φ_1, φ_2) = ρ(φ_1), ρ_2(φ_1, φ_2) = ρ(φ_2)$}, (2.5) where {$ρ$} is the natural representation.

Gamma matrices generate a matrix representation of {$Cl_{1,3}(\mathbb{R})$}. Higher-dimensional gamma matrices can be constructed recursively.

{$\mathbb{R}$} represented as {$(r)$}

{$\mathbb{C}$} represented as {$\begin{pmatrix}a & b \\ -b & a\end{pmatrix}\begin{pmatrix}c & d \\ -d & c\end{pmatrix}=\begin{pmatrix}ac-bd & ad+bc \\ -(ad+bc) & ac-bd\end{pmatrix}$}

{$\mathbb{R}\oplus\mathbb{R}$} represented as {$\begin{pmatrix}a & b \\ b & a\end{pmatrix}\begin{pmatrix}c & d \\ d & c\end{pmatrix}=\begin{pmatrix}ac+bd & ad+bc \\ ad+bc & ac+bd\end{pmatrix}$}

Alternatively, represented as {$\begin{pmatrix}a+b & 0 \\ 0 & a-b\end{pmatrix}\begin{pmatrix}c+d & 0 \\ 0 & c-d\end{pmatrix}=\begin{pmatrix}(ac+bd)+(ad+bc) & 0 \\ 0 & (ac+bd)-(ad+bc)\end{pmatrix}$}

Or consider this: A Clifford module {$M$} over the Clifford algebra {$\mathbb{R}\oplus\mathbb{R}$} is either the trivial representation

{$(a,b)\rightarrow (a)$} which sends both {$1=(1,1)$} and {$e_1=(1,-1)$} to {$(1)$}

or the alternating representation

{$(a,b)\rightarrow (b)$} which sends {$1=(1,1)$} to {$(1)$} and {$e_1=(1,-1)$} to {$(-1)$}

Is that wrong?

{$\mathbb{H}=\{a+bi+cj+dk\}$} represented as {$\begin{pmatrix}a+bi & c+di \\ -c+di & a-bi\end{pmatrix}$}

q mod 8	representation	dimension	irreducible representation spaces
-2	{$\mathbb{R}(2)$}	Normal	{$2^1$}	unique
-1	{$\mathbb{R}\oplus\mathbb{R}$}	Normal	{$2^0$}	two: {$\tilde\gamma_\mu=-\gamma_\mu$}
0	{$\mathbb{R}$}	Normal	{$2^0$}	unique
1	{$\mathbb{C}$}	Almost complex	{$2^0$}	unique
2	{$\mathbb{H}$}	Quaternionic	{$2^2$}	unique
3	{$\mathbb{H}\oplus\mathbb{H}$}	Quaternionic	{$2^2$}	two: {$\tilde\gamma_\mu=-\gamma_\mu$}
4	{$\mathbb{H}(2)$}	Quaternionic	{$2^3$}	unique
5	{$\mathbb{C}(2)$}	Almost complex	{$2^3$}	unique

读物

• Definition of Irreducible Graded Z2-Modules
• Dale Husemoller. Fiber Bundles. Chapter 11 presents Bott periodicity in the complex case. Chapter 12 presents Clifford algebras, and Section 6 (pages 161-166) presents Clifford modules, including graded representations.
• Math StackExchange: Definition of {$\mathbb{Z}_2$}-graded module homomorphism
• Parshall. Some Z2-Graded Representation Theory

The {$\mathbb{Z}_2$} grading is inherent because the Clifford algebra is constructed by modding out by the equation {$\phi(x)^2=-Q(x)1_A$}, which respects the even and odd distinction, but destroys the integer grading.

A module {$M$} over an algebra {$A$} is simply the module {$M$} over the ring {$A$}.

A left {$A$}-module {$M$} consists of an abelian group {$(M, +)$} and an operation {$· : A × M → M$} such that for all {$a_1, a_2$} in {$A$} and {$x, y$} in {$M$}, we have

• {$a\cdot (x+y)=a\cdot x+a\cdot y$}
• {$(a_1+a_2)\cdot x=a_1\cdot x+a_2\cdot x$}
• {$(a_1a_2)\cdot x=a_1\cdot (a_2\cdot x)$}
• {$ 1\cdot x=x $}

A {$\mathbb{Z}_2$}-graded module {$M$} over a {$\mathbb{Z}_2$}-graded algebra {$A$} is an {$A$}-module {$M$} with {$M=M^0\oplus M^1$} such that {$A^iM^j\subset M^{i+j}$} for {$i,j\in\mathbb{Z}_2$}. Thus we have even maps even to even; even maps odd to odd; odd maps even to odd; odd maps odd to even.

A Clifford module is a {$\mathbb{Z}_2$}-graded module {$M$} over a Clifford algebra {$C(f)$}.

For example, a Clifford module {$M$} over the Clifford algebra {$\mathbb{C}$} is the usual representation

{$\begin{pmatrix}a & -b \\ b & a\end{pmatrix}$} where elements {$\begin{pmatrix}a & 0 \\ 0 & a\end{pmatrix}$} are even and {$\begin{pmatrix}0 & -b \\ b & 0\end{pmatrix}$} are odd.

What does a (graded!) Clifford module {$M$} over the Clifford algebra {$\mathbb{R}\oplus\mathbb{R}$} look like?

As noted above, from Wedderburn's theorem, {$\mathbb{R}$}, {$\mathbb{C}$} and {$\mathbb{H}$} have unique irreducible representations. These are also unique {$\mathbb{Z}_2$}-graded modules.

{$\mathbb{R}\oplus\mathbb{R}$} has two irreducible representations mapping one or the other summand to zero. Likewise for {$\mathbb{C}\oplus\mathbb{C}$} and {$\mathbb{H}\oplus\mathbb{H}$}.

The inclusion {$i:C_k\rightarrow C_{k+1}$} induces a map {$i^*:M(C_{k+1})\rightarrow M(C_k)$}. This latter map means that a graded representation of {$M(C_{k+1})$} can be restricted to a graded representation of {$M(C_k)$}. It then may be that the original representation is irreducible whereas the restriction is reducible. This happens to the unique representation of {$\mathbb{C}$} when it is restricted to a representation of {$\mathbb{R}$}, as here:

{$\begin{pmatrix}a & -b \\ b & a\end{pmatrix}$} is restricted to {$\begin{pmatrix}a & 0 \\ 0 & a\end{pmatrix}$}

Thus the unique irreducible representation of {$\mathbb{C}$} gets mapped by {$i^*$} to two copies of the unique irreducible representation of {$\mathbb{R}$}.

Similarly, this happens for the unique irreducible representation (over the reals) of {$\mathbb{H}$}, which gets mapped by {$i^*$} to two copies of the unique irreducible representation (over the reals) of {$\mathbb{C}$}.

Consider the two representations of {$\mathbb{R}\oplus\mathbb{R}$}

Note that {$M(C_{k+1})\cong N(C_{k+1}^0)\cong N(C_{k})$}.

How do we make sense of a map from the ungraded representations {$N(C_{k})$} to the graded representations {$M(C_k)$}?

• Steven Lehar - website
• Steven Lehar at PhilPeople
• Syllabus: Roberto Rubio. Clifford algebras, spinors, and applications
• Course materials: Roberto Rubio. Clifford algebras, spinors and applications
• Ying-Qiu Gu. Some Applications of Clifford Algebra in Geometry.

Pierre Renaud. Clifford Algebras. Lecture Notes on Applications in Physics.

Basil Hiley

• Basil Hiley website and contacts
• Hierarchy of Clifford algebras
• Hiley expanded on the notion of a process algebra as proposed by Hermann Grassmann and the ideas of distinction[81] of Louis H. Kauffman. He took reference to the vector operators introduced by Mário Schönberg in 1957[113] and by Marco Fernandes in his PhD thesis of 1995, who had constructed orthogonal Clifford algebras for certain pairs of dual Grassmann algebras. Adopting a similar approach, Hiley constructed algebraic spinors as minimal left ideals of a process algebra built on the Kauffman's notion of distinction. http://www.birkbeck.ac.uk/tpru/BasilHiley/14MomentsANPA2001W.pdf
• Basil Hiley. Towards a Dynamics of Moments: The Role of Algebraic Deformation and Inequivalent Vacuum States.
• B.J.Hiley, R.E.Callaghan. The Clifford Algebra approach to Quantum Mechanics A: The Schroedinger and Pauli Particles.
• Basil Hiley. Mind and matter: aspects of the implicate order described through algebra.
• Basil Hiley. Process, Distinction, Groupoids and Clifford Algebras: an Alternative View of the Quantum Formalism.
• D. Bohm and B. J. Hiley. Generalisation of the twistor to Clifford algebras as a basis for geometry.
• https://en.wikipedia.org/wiki/John_Archibald_Wheeler
• https://en.wikipedia.org/wiki/Process_philosophy Whitehead's Process and Reality
• https://en.wikipedia.org/wiki/Process_calculus (computer science)
• Ying-Qiu Gu. Application of Clifford Algebra in Solving the Eigen Equations of Quantum Mechanics.
• https://johncarlosbaez.wordpress.com/2023/04/26/bosons-fermions-and-clifford-algebras/

Fermionic minimal answer is "yes or no": -1/2 (no) or +1/2 (yes). Bosonic spin-0 minimal answer is "I don't know" 0. Spin-1 has three answers. Spin-2 for the graviton has five answers, as with the fivesome. Thus spin can express divisions of everything. Study spinors and Clifford algebras. Relate to angular momentum.

• Christian Voigt: Clifford algebras, Fermions and categorification

• Wikipedia: Higher Clifford Algebras 24 periodicity of 3-categories
• Geoffrey Dixon. Division Algebras, Clifford Algebras, Periodicity "Using novel representations of the purely Euclidean Clifford algebras over all four of the division algebras, R, C, H, and O, a door is opened to a Clifford algebra periodicity of order 24 as well."

Generalized Clifford Algebra has clock-shift operators.

• Some matrices describe the 8-cycle clock (the trolley stops).
• Generalized Pauli matrices describe the 3 shifts (the trolley cars of different increments +1, +2, +3). See the "clock and shift matrices".

{$\begin{pmatrix} & & \mathbb{C}_{n} & & \\ & \mathbb{H}_{n} & & \mathbb{R}_{n} & \\ \mathbb{H}_{n} \times \mathbb{H}_{n} & & & & \mathbb{R}_{n} \times \mathbb{R}_{n} \\ & \mathbb{H}_{n} & & \mathbb{R}_{n} & \\ & & \mathbb{C}_{n} & & \end{pmatrix}$}

• Eight-cycle
  • The fourfold periodicity within the Bott periodicity is a repeating pattern (0,1,1,0 ?)
  • W: Symmetric group Note that the reverse on n elements and perfect shuffle on 2n elements have the same sign; these are important to the classification of Clifford algebras, which are 8-periodic.
  • This pattern is based on the sign of the pseudoscalar.
  • This pattern expresses whether the sum of 1+...+n is even or odd. Even + even = even; + odd = odd; + even = odd; + odd = even; and so on. This pattern is likewise the sum of the numbers mod 2. Thus 0+0=0; +1=1; +0=1;+1=0.
  • This pattern also comes up in multiplying by i. We get 1, i, -1, -i - two positives followed by two negatives.
  • A similar pattern comes up in the volumes of n-spheres. The volume of an n-sphere is {$\frac{\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)}$} where {$\Gamma(n+\frac{1}{2})=(n-\frac{1}{2})(n-\frac{3}{2})\cdots \frac{1}{2}\cdot\pi^{\frac{1}{2}}$}. Thus we have: {$\frac{2n}{2}=n, \frac{2n+1}{2}-\frac{1}{2}=n, \frac{2n+2}{2}=n+1, \frac{2n+3}{2}-\frac{1}{2}=n+1$}, and so on.
  • The pattern also comes up by two recurrences for volume and hyperarea (surface area) in terms of each other. Starting with {$V_0(R)=1, A_0(R)=2$} and continuing {$V_{n+1}(R)=\frac{R}{n+1}A_{n}(R), A_{n+1}(R)=(2\pi R) V_{n}$} we get the pattern for the factor {$\pi$}.

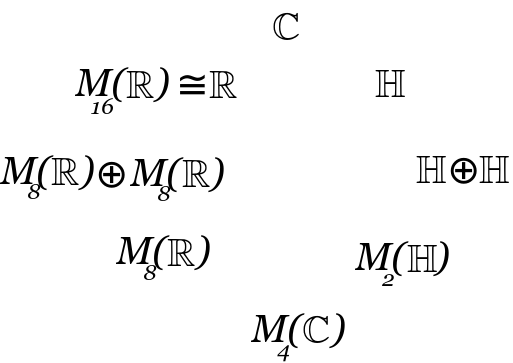
• The pseudoscalar (the product of all the basis elements) is important because it is similar to the scalar. When the dimension is odd, then the pseudoscalar commutes with everything, and so it is in the center. When the dimension is even, then the pseudoscalar does not commute with everything and so the center only consists of the identity.
• In the real case, what characterizes the Clifford algebra of signature {$(p,q)$} is the number {$p-q \text{mod} 8$}.
• There are the progressions, adding basis elements which square to {$-1$}, but likewise in the {$+1$} direction:
  • Complexification:

{$$R, C, H$$}

• Growing:

{$$R, R \bigoplus R, \begin{pmatrix} R & R \\ R & R \end{pmatrix} $$}

• Untangling:

{$$ H, \begin{pmatrix} C & C \\ C & C \end{pmatrix}, \begin{pmatrix} R & R & R & R \\ R & R & R & R \\ R & R & R & R \\ R & R & R & R \end{pmatrix} $$}

• Wedderburn's theorem states that The Artin-Wedderburn theorem generalizes this result to Artinian rings.
• Frobenius's theorem for real division algebras states that every finite-dimensional associative division algebra over the real numbers is isomorphic to the real numbers, the complex numbers or the quaternions.
• Hurwitz's theorem: The only real normed division algebras are R, C, H, and the (non-associative) algebra O.
• A division algebra is an algebra over a field in which division, except by zero, is always possible.
• C0 R
• C1 C
• C2 H
• C3 H + H
• C4 H(2)
• C5 C(4)
• C6 R(8)
• C7 R(8) + R(8)
• C8 R(16)

{$C_{n+8}$} consists of 16 x 16 matrices with entries in {$C_n$}.

• The positive and negative directions (for the signature) are related as {$R$} and {$M_8(R)$}.
• For any n=s+t (exploring how we generate the perspectives in a division of everything into n perspectives, going from 0 to n in n steps) there are two patterns:
  • even n, {$X=2^{\frac{N}{2}}$}: {$\dots R(2X), R(2X), H(X), H(X), R(2X), R(2X), H(X), H(X) \dots$}
  • odd n, {$X=2^{\frac{N-1}{2}}$}: {$\dots H(X)\bigoplus H(X), C(2X), R(2X)\bigoplus R(2X), C(2X), H(X)\bigoplus H(X), C(2X), R(2X)\bigoplus R(2X) \dots$}
• Combined, these two patterns yield for n, along the edge:
  • {$\dots R(2^N), C(2^N), H(2^N), H(2^N) \bigoplus H(2^N), H(2^{N+1}), C(2^{N+2}), R(2^{N+3}), R(2^{N+3})\bigoplus R(2^{N+3}) \dots$}

Complex structures

• We call {$J$} a complex structure on {$R^n$} if {$J\in O(n)$} and {$J^2=−I_n$}. Denote the space of complex structures {$Ω_1(n)⊂O(n)$}.
• Define {$Ω_k(n)$} to be the space of complex structures that anti-commute with fixed {$J_1,\dots ,J_{k-1}$}.
• {$Ω_0 \cong Ω_8$}
• Consider how complex structures relate to divisions of everything. Apparently, each {$J_i$} is a perspective. Anti-commutativity {$J_iJ_j = -J_jJ_i$} means that the composition of perspectives is inverted if the order is switched. So the matrix {$-I$} can be interpreted as an inversion of perspective, and thus, of chains of perspectives. A set of eight perspectives brings us back to no perspectives, which is to say, the default perspective at the origin.
• Clifford modules are representations of Clifford algebras.

Real Clifford algebra consists of roots of -1 that all anticommute. Complex Clifford algebra adds an additional root of -1 that commutes with all of those other roots.

wrong...

• R nullsome
• C nullsome
• H twosome 1+i (different) j+ij (the same)
• H+H threesome splits the twosome
• (H2) foursome - internally doubles
• (C4) foursome
• (R8) sixsome
• R+R sevensome (dividing the nullsome into two perspectives)

(S16) what would S mean? half of R? positive reals?

• For Clifford algebras we have {$e_ie_j=-e_je_i$} but what does that mean in the case {$i=j$}? It would mean {$e_i^2=0$} which is the degenerate case.
• Think of tenfold way for Standard Model (per Cohl Furey)(relating R,C,H,O by analogy to four DNA bases) as {$M_{\mathbb{R}\otimes\mathbb{C}\otimes\mathbb{H}\otimes \mathbb{O}}\cong M_{32}(\mathbb{C})\cong \mathbb{C}l(10) \cong Cl(8)\otimes \mathbb{C}l(2) \cong Cl(0,8)\otimes Cl(3,0) $} where {$\mathbb{C}l(n)$} indicates a complex Clifford algebra. Standard Model off-shell states given by {$Cl(0,8)$} and three-dimensional {$Cl(3,0)$} which grounds three-dimensionality of space.
• Combinatorial interpretation of {$+$} and {$-$} signs in Clifford algebras. Are you facing, reading right (positive) or left (negative)? Assign to each element a direction.
• For Clifford algebras, the grading, odd or even, is describing whether you include or not a generator, whether you are stepped out (if there is no generator) or stepped in (if there is a generator). Every division of everything has one perspective where it's only stepped in and another perspective which is not included where you are completely stepped out. So for example, R is completely stepped out and that's God. Everything is 1 + e_1, the complex numbers, where it is stepped out but also stepped in.
• Note that these are complementing each other, the generators that square to -1 (they are giving the divisions) and that square to +1 (that complement the divisions and are what God sees and we don't)
• Louis Kauffman. A Construction for Clifford Algebras.
• Eigenchris, Chapter 25+ of Road to Reality. 25:00. How to solve {$i^2=-1$}? By decree - internal structure - defining {$i$} as a new symbol. Or by construction, which leads to thinking of i and 1 as matrices.
• Each kth perspective in a Clifford algebra corresponds to a kth level in the hierarchy of products of n perspectives, thus chains of length k of n perspectives, which are built up from the very same n perspectives. Each level in the hierarchy has a qualititative structural meaning in terms of the perspectives and the whole.
• Clifford algebras establish perspectives. You can look at the same thing - the same algebra {$R(2)$} - from noncomparable perspectives - as Clifford algebras {$Cl_{1,1}$} and {$Cl_{2,0}$}.
• Generators {$a_j$} for which {$a_j^2=1$} are experienced directly whereas generators {$b_j$} for which {$b_j^2=-1$} express the change in direction upon reflection, thus stepped out.

Contact

• https://www.ff.vu.lt/tfai/darbuotojai/acus

Readings

• Logan Lim. Why Geometric Algebra Should be in Standard Linear Algebra Curriculum.
• Are Clifford algebras and differential forms equivalent frameworks for differential geometry?
• John Baez about Clifford algebra periodicity
• John Baez also Clifford algebra periodicity
• Attiyah, Bott, Shapiro. Clifford Modules. 1963.
• 维基百科: Clifford paralells and quaternions
• Dan Piponi. Constructing Clifford Algebras using the Super Tensor Product.
• John Baez. Clifford Algebras and the octonions
• Tammo. Representation Theory. Chapter 3 Wedderburn Theorem
• W: Classification of Clifford algebras
• Baez: Clifford algebra periodicity
• H. Blaine Lawson, Jr. and Marie-Louise Michelson, "Spin Geometry", Princeton U. Press, Princeton, 1989. (For proof)
• Dale Husemoller, "Fibre Bundles", Springer-Verlag, Berlin, 1994. (For proof)
• Jayme Vaz, Jr., Roldão da Rocha, Jr. An Introduction to Clifford Algebras and Spinors.

Questions