Math 4 Wisdom. "Mathematics for Wisdom" by Andrius Kulikauskas. | Research / BottPeriodicityForOctonionManiacs

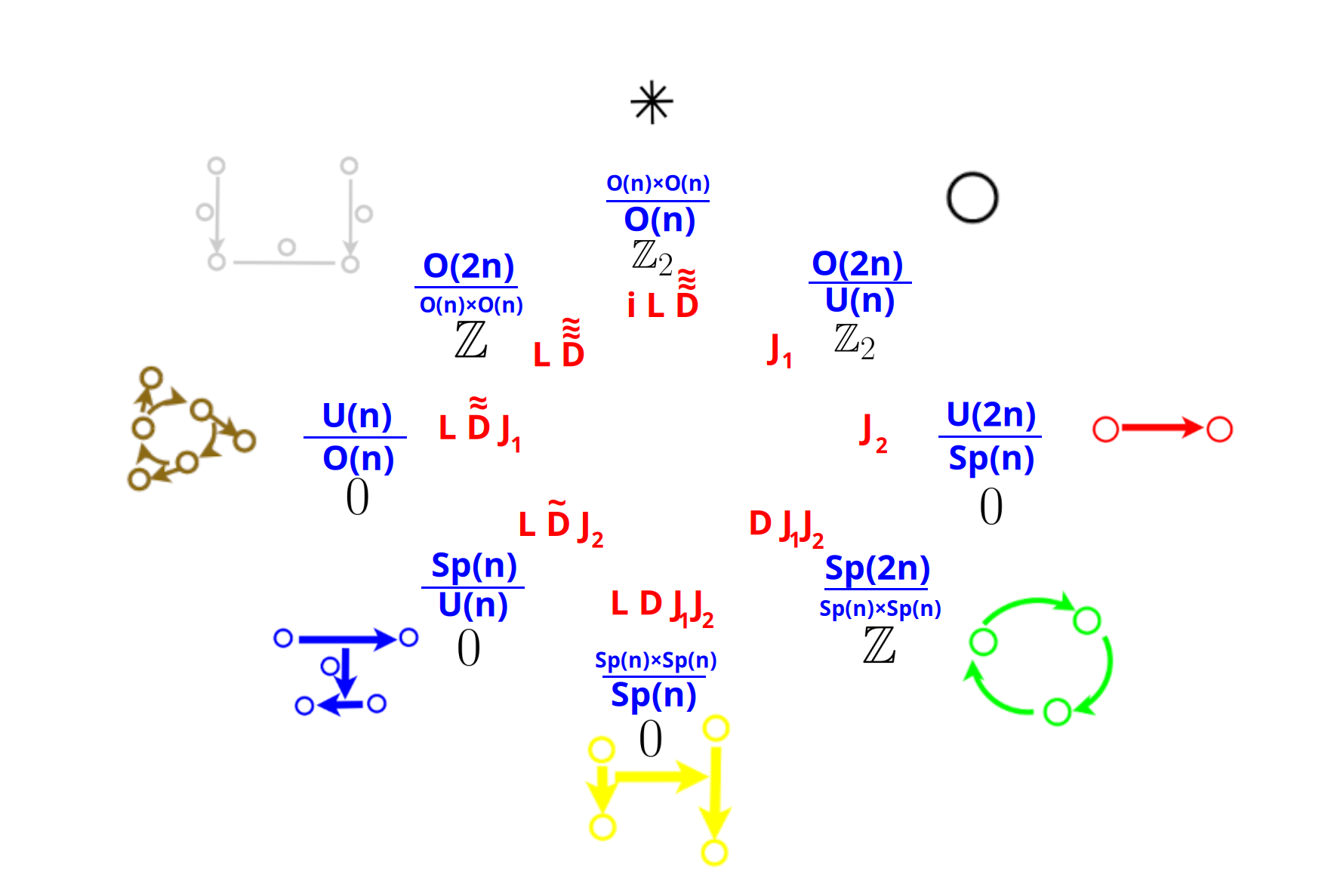
Bott periodicity, Sets of Linear Complex Structures, Artificial General Intelligence Presentation, Hamiltonians

2025.03.03 Andrius Kulikauskas. Math4Wisdom.com

Metaphysics of Bott Periodicity for Octonion Maniacs

Metaphysics	Mathematics
everything	orthogonal group {$O(16r)$}
perspective	linear complex structure {$J_\alpha$}
division of everything	set of mutually anticommuting {$J_1,J_2,J_3,\dots$}
shift in perspective	isometry {$L=J_\alpha J_\beta$} (of different sizes?)
three-cycle	quaternions {$i, j, k$} but in both directions thanks to {$D$}
foursome	isometry {$LD$} maps {$J_1J_2$} from one space to another
higher divisions	ręmove {$J_1, J_2, J_1J_2$} from the total {$LDJ_1J_2$}
collapse of everything	second isometry {$Q$}

2017. Andrius Kulikauskas. Time and Space as Representations of Decision-Making.

John Baez. The Octonions. Projective lines.

Given a vector space {$V$} over a field {$K$}. The projective space {$P(V)$} is the set of equivalence classes of {$x\in V, x\neq 0$} defined by {$x\sim y$} if there exists {$λ\in K$} such that {$x = λy$}.

A projective line is a one-dimensional projective space. All of the points lie on a single line. The line includes a point at infinity.`

{$\mathbb{RP}^1\cong S^1$}
{$\mathbb{CP}^1\cong S^2$}
{$\mathbb{HP}^1\cong S^4$}
{$\mathbb{OP}^1\cong S^8$}

{$f_\mathbb{R}:S^0\to O(1)$}
{$f_\mathbb{C}:S^1\to O(2)$}
{$f_\mathbb{H}:S^3\to O(4)$}
{$f_\mathbb{O}:S^7\to O(8)$}

{$[f_\mathbb{R}]$} generates {$\pi_0(O(\infty)) \cong \mathbb{Z}_2$}
{$[f_\mathbb{C}]$} generates {$\pi_1(O(\infty)) \cong \mathbb{Z}_2$}
{$[f_\mathbb{H}]$} generates {$\pi_3(O(\infty)) \cong \mathbb{Z}$}
{$[f_\mathbb{O}]$} generates {$\pi_7(O(\infty)) \cong \mathbb{Z}$}

{$S^0\hookrightarrow S^1\hookrightarrow S^1$}
{$S^1\hookrightarrow S^3\hookrightarrow S^2$}
{$S^3\hookrightarrow S^7\hookrightarrow S^4$}
{$S^7\hookrightarrow S^{15}\hookrightarrow S^8$}

John Baez. The Octonions. {$\mathbb{OP}^1$} and Bott Periodicity.

Real vector bundle {$E$} over {$S^n$} defines an equivalence class {$[E]\in KO(S^n)$} generating an additive monoid that yields the Grothendieck group {$KO(S^n)$}. Fixing a point in {$S^n$} and modding out by the dimension of the fiber of {$E$} at that point yields the reduced theory {$\widetilde{KO}(S^n)$}.

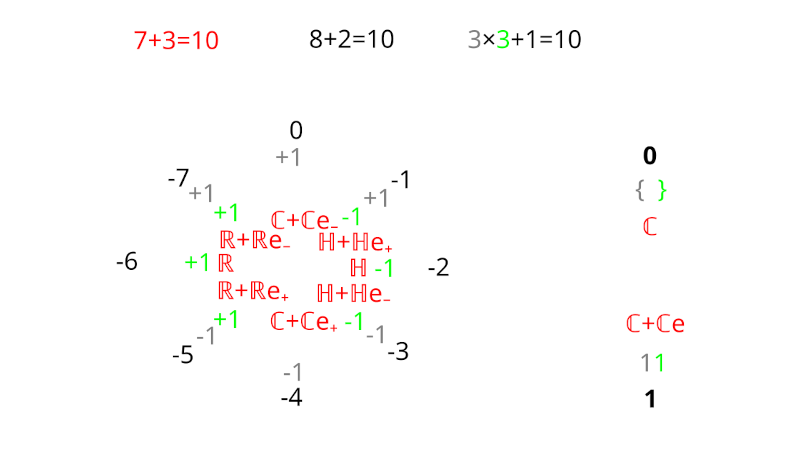
Reduced real K-theory of spheres

{$\widetilde{KO}(S^1)$}	{$\widetilde{KO}(S^2)$}	{$\widetilde{KO}(S^3)$}	{$\widetilde{KO}(S^4)$}	{$\widetilde{KO}(S^5)$}	{$\widetilde{KO}(S^6)$}	{$\widetilde{KO}(S^7)$}	{$\widetilde{KO}(S^8)$}
{$\mathbb{Z}_2$}	{$\mathbb{Z}_2$}	{$0$}	{$\mathbb{Z}$}	{$0$}	{$0$}	{$0$}	{$\mathbb{Z}$}

Projective lines

{$[L_\mathbb{R}]$} generates {$\widetilde{KO}(S^1)\cong \mathbb{Z}_2$}
{$[L_\mathbb{C}]$} generates {$\widetilde{KO}(S^2)\cong \mathbb{Z}_2$}
{$[L_\mathbb{H}]$} generates {$\widetilde{KO}(S^4)\cong \mathbb{Z}$}
{$[L_\mathbb{O}]$} generates {$\widetilde{KO}(S^8)\cong \mathbb{Z}$}

There is a graded ring {$KO$} given by {$KO_n=\widetilde{KO}(S^n)$} and the smash product of spheres.

Multiplying by {$[L_\mathbb{O}]$} gives the isomorphism {$\widetilde{KO}(S^n)\to\widetilde{KO}(S^n)$} defined by {$x\mapsto [L_\mathbb{O}]x$}.

J.-H.Eschenburg. Geometry of Octonions

Standard basis {$B_\mathbb{O} = \{1, i, j, k, l, il, jl, kl\}$}

Periodicity Theorem for Clifford modules: {$M_{n+8}=M_n\otimes \mathbb{O}^2$}

Michael Stone, Ching-Kai Chiu, Abhishek Roy. Symmetries, Dimensions, and Topological Insulators: the mechanism behind the face of the Bott clock.

{$O(16)\supset U(8)\supset Sp(4)\supset Sp(2)\times Sp(2)\supset Sp(2)\supset U(2)\supset O(2)\supset O(1)\times O(1)\supset O(1)$}

Define {$J_1, J_2, J_3, J_4, J_5, J_6, J_7, J_8, \dots$}

that are orthogonal matrices {$J_\alpha J_\alpha^T=I$}
that are independent generators
such that {$J_\alpha^2=-1$} (thus {$J_\alpha^{T}=J_\alpha^{-1}=-J_\alpha$} and so {$J_\alpha$} are skew-symmetric)
{$J_\alpha J_\beta = -J_\beta J_\alpha$} when {$\alpha\neq\beta$}.

{$(J_1 J_2)(J_1 J_2)=-1$}

{$(J_1 J_2 J_3)(J_1 J_2 J_3)=1$} Thus the operator {$J_1J_2J_3$} satisfies {$x^2–1=0$} and its eigenvalues are in {$\{1,-1\}$}.

{$K=\begin{pmatrix} I_4 & \\ & -I_4 \\ \end{pmatrix}$}, {$L=J_3J_4=\begin{pmatrix} & I_4 \\ -I_4 & \\ \end{pmatrix}$}, {$KL=\begin{pmatrix} & I_4 \\ I_4 & \\ \end{pmatrix}$},

{$K=J_1J_2J_3=\textrm{diag}[-1,-1,-1,-1,1,1,1,1]$}
{$M=J_1J_4J_5=\textrm{diag}[-1,-1,1,1,1,1,-1,-1]$}
{$N=J_2J_4J_6=\textrm{diag}[1,-1,1,-1,-1,1,-1,1]$}
{$P=J_1J_6J_7=\textrm{diag}[\hat{r},\hat{r},-\hat{r},-\hat{r},\hat{r},\hat{r},-\hat{r},-\hat{r}]$}
{$Q=J_7J_8=\textrm{diag}[\hat{i},\hat{i},\hat{i},\hat{i},\hat{i},\hat{i},\hat{i},\hat{i}]$} where

{$\hat{r}=\begin{pmatrix}1 & 0\\0 & -1\\ \end{pmatrix}, \hat{i}=\begin{pmatrix}0 & -1\\1 & 0\\ \end{pmatrix}$}

They provide a recipe for constructing mutually anticommuting linear complex structures {$J_1, J_2, J_3, J_4, J_5, J_6, J_7,\cdots$}.

{$J_1=\textrm{diag}[\hat{i}]$}

{$J_2=\textrm{diag}[j_4]$}

Suppose {$J_3$} exists. Let {$K=J_1J_2J_3$}. Then {$K^2=I$} and consequently, {$K$} satisfies {$x^2-1$}, thus posseses quaternionic eigenspaces {$V_{\pm}$} where it takes values {$\pm 1$} accordingly. {$Kv_+=v_+$} for {$v_+\in V_+$} and {$Kv_-=-v_-$} for {$v_-\in V_-$}. {$K$} can be used to define {$J_3=J_2^{-1}J_1^{-1}K$}.

To define {$J_4$} we must suppose {$V_+$} and {$V_-$} have the same dimension. Suppose {$J_4$} exists. Let {$L=J_3J_4$}. Then {$LK=-KL, L^2=-I, LJ_1=J_1L, LJ_2=J_2L$}. {$L$} preserves the quaternionic structure and is a quaternionic isometry from {$V_+$} to {$V_-$}. {$L$} can be used to define {$J_4=J_3^{-1}L$}.

Suppose {$J_5$} exists. Let {$M=J_1J_4J_5$}. Then {$M^2=I$} and {$M$} commutes with {$K$} and {$J_1$}. Thus {$M$} acts within an eigenspace of {$K$} (say {$V_+$}) and divides it into two mutually orthogonal eigenspaces {$W_\pm$} with {$W_-=J_2W_+$}. {$M$} can be used to define {$J_5=J_4^{-1}J_1^{-1}M$}.

Suppose {$J_6$} exists. Let {$N=J_2J_4J_6$}. Then {$N^2=I$} and {$N$} commutes with {$K$} and {$M$}. Thus {$N$} acts within an eigenspace of {$M$} (say {$W_+$}) and divides it into two mutually orthogonal eigenspaces {$X_\pm$} with {$X_-=J_1W_+$}. {$N$} can be used to define {$J_6=J_4^{-1}J_2^{-1}N$}.

Suppose {$J_7$} exists. Let {$P=J_1J_6J_7$}. Then {$P^2=I$} and {$P$} commutes with {$K$}, {$M$} and {$N$}. Thus {$P$} acts within an eigenspace of {$X$} (say {$X_+$}) and divides it into two mutually orthogonal eigenspaces {$Y_\pm$}. {$P$} can be used to define {$J_7=J_6^{-1}J_1^{-1}P$}.

To define {$J_8$} we must suppose {$Y_+$} and {$Y_-$} have the same dimension. Suppose {$J_8$} exists. Let {$Q=J_7J_8$}. Then {$Q^2=-I$} and {$Q$} commutes with {$K$}, {$M$} and {$N$} but anticommutes with {$P$}. Thus {$Q$} is an isometry mapping {$Y_+\leftrightarrow Y_-$}. {$Q$} can be used to define {$J_8=J_7^{-1}Q$}.

{$J_1= \begin{pmatrix} & -1 & & & & & & \\ 1 & & & & & & & \\ & & & -1 & & & & \\ & & 1 & & & & & \\ & & & & & -1 & & \\ & & & & 1 & & & \\ & & & & & & & -1 \\ & & & & & & 1 & \\ \end{pmatrix}$}	{$J_2= \begin{pmatrix} & & 1 & & & & & \\ & & & -1 & & & & \\-1 & & & & & & & \\ & 1 & & & & & & \\ & & & & & & 1 & \\ & & & & & & & -1 \\ & & & & -1 & & & \\ & & & & & 1 & & \\ \end{pmatrix}$}	{$J_3= \begin{pmatrix} & & & -1 & & & & \\ & & -1 & & & & & \\ & 1 & & & & & & \\ 1 & & & & & & & \\ & & & & & & & 1 \\ & & & & & & 1 & \\ & & & & & -1 & & \\ & & & & -1 & & & \\ \end{pmatrix}$}
{$J_1$} yields {$\mathbb{C}$}	adding {$J_2$} yields {$\mathbb{H}$}	adding {$J_3$} yields {$\mathbb{H}\oplus\mathbb{H}$}
{$J_4= \begin{pmatrix} & & & & & & & 1 \\ & & & & & & 1 & \\ & & & & & -1 & & \\ & & & & -1 & & & \\ & & & 1 & & & & \\ & & 1 & & & & & \\ & -1 & & & & & & \\ -1 & & & & & & & \\ \end{pmatrix}$}	{$J_5= \begin{pmatrix} & & & & & & -1 & \\ & & & & & & & 1 \\ & & & & -1 & & & \\ & & & & & 1 & & \\ & & 1 & & & & & \\ & & & -1 & & & & \\ 1 & & & & & & & \\ & -1 & & & & & & \\ \end{pmatrix}$}	{$J_6= \begin{pmatrix} & & & & & 1 & & \\ & & & & 1 & & & \\ & & & & & & & 1 \\ & & & & & & 1 & \\ & -1 & & & & & & \\-1 & & & & & & & \\ & & & -1 & & & & \\ & & -1 & & & & & \\ \end{pmatrix}$}
adding {$J_4$} yields {$M_2(\mathbb{H})$}	adding {$J_5$} yields {$M_4(\mathbb{C})$}	adding {$J_6$} yields {$M_8(\mathbb{R})$}
{$J_7= \begin{pmatrix} & & & & \hat{r} & & & \\ & & & & & -\hat{r} & & \\ & & & & & & -\hat{r} & \\ & & & & & & & \hat{r} \\-\hat{r} & & & & & & & \\ & \hat{r} & & & & & & \\ & & \hat{r} & & & & & \\ & & & -\hat{r} & & & & \\ \end{pmatrix}$}	{$J_8= \begin{pmatrix} & & & & \hat{i}\hat{r} & & & \\ & & & & & -\hat{i}\hat{r} & & \\ & & & & & & -\hat{i}\hat{r} & \\ & & & & & & & \hat{i}\hat{r} \\-\hat{i}\hat{r} & & & & & & & \\ & \hat{i}\hat{r} & & & & & & \\ & & \hat{i}\hat{r} & & & & & \\ & & & -\hat{i}\hat{r} & & & & \\ \end{pmatrix}$}	\begin{matrix}1=\begin{pmatrix} 1 & \\ & 1 \\ \end{pmatrix} & \hat{i}=\begin{pmatrix} & -1 \\ 1 & \\ \end{pmatrix} \\ & \\ \hat{r}=\begin{pmatrix} 1 & \\ & -1 \\ \end{pmatrix} & \hat{i}\hat{r}=\begin{pmatrix} & 1 \\ 1 & \\ \end{pmatrix}\\ \end{matrix}
adding {$J_7$} yields {$M_8(\mathbb{R})\oplus M_8(\mathbb{R})$}	adding {$J_8$} yields {$M_{16}(\mathbb{R})$}	Notation: {$1, \hat{i}, \hat{r}, \hat{i}\hat{r}$}

Can we express {$(a,b)\in M_8(\mathbb{R})\oplus M_8(\mathbb{R})$} in terms of {$2\times 2$} matrices {$\begin{pmatrix} a & \\ & b \\ \end{pmatrix}$} ? What problem do we run into if we want to define {$J_7$}?

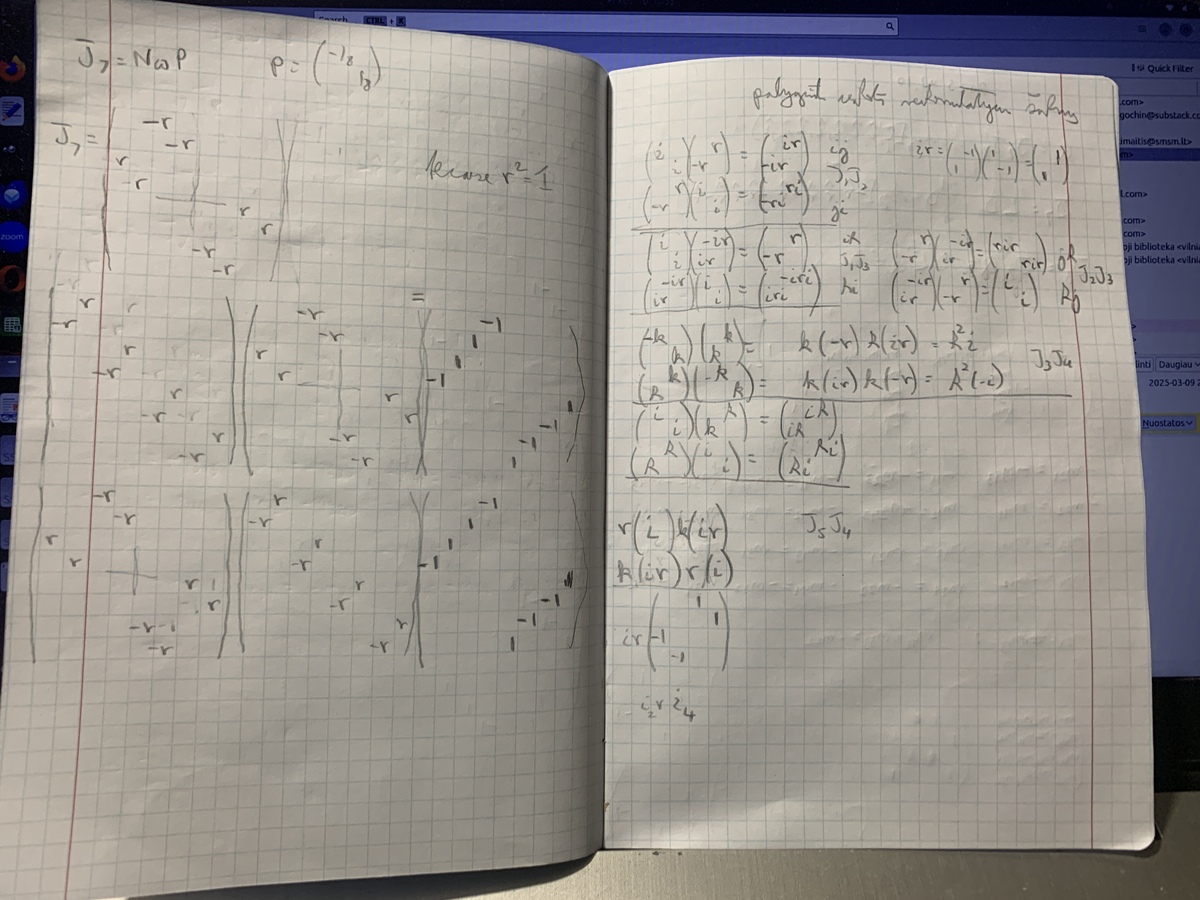{$J_4=LJ_1J_2\;\textrm{diag} \begin{bmatrix} -1 & -1 & -1 & -1 & 1 & 1 & 1 & 1 \\ \end{bmatrix}$}

{$J_5=LJ_2\;\textrm{diag} \begin{bmatrix} 1 & 1 & -1 & -1 & 1 & 1 & -1 & -1 \\ \end{bmatrix}$}

{$J_6=LJ_1\;\textrm{diag} \begin{bmatrix} 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\ \end{bmatrix}$}

{$J_7=L\;\textrm{diag} \begin{bmatrix} 1 & -1 & -1 & 1 & -1 & 1 & 1 & -1 & 1 & -1 & -1 & 1 & -1 & 1 & 1 & -1 \\ \end{bmatrix}$}

Notation

{$R_2= \begin{pmatrix} 1 & \\ & -1 \end{pmatrix}, R_4= \begin{pmatrix} 1 & & & \\ & 1 & & \\ & & -1 & \\ & & & -1 \\ \end{pmatrix}, R_8=\begin{pmatrix} 1 & & & & & & & \\ & 1 & & & & & & \\ & & 1 & & & & & \\ & & & 1 & & & & \\ & & & & -1 & & & \\ & & & & & -1 & & \\ & & & & & & -1 & \\ & & & & & & & -1 \\ \end{pmatrix}$}

The reflections {$R_2, R_4, R_8$} determine eigenspaces {$V_{+1}$} and {$V_{-1}$}.

A shift in perspective is given by an isometry between eigenspaces {$V_{+1}$} and {$V_{-1}$}.

{$L_2= \begin{pmatrix} & -1 \\ 1 & \end{pmatrix}, L_4= \begin{pmatrix} & & -1 & \\ & & & -1 \\ 1 & & & \\ & 1 & & \\ \end{pmatrix}, L_8=\begin{pmatrix} & & & & 1 & & & \\ & & & & & 1 & & \\ & & & & & & 1 & \\ & & & & & & & 1 \\ -1 & & & & & & & \\ & -1 & & & & & & \\ & & -1 & & & & & \\ & & & -1 & & & & \\ \end{pmatrix}$}

Note that

{$\begin{pmatrix} & -1 & & \\ 1 & & & \\ & & & -1 \\ & & 1 & \\ \end{pmatrix} \begin{pmatrix} & & 1 & \\ & & & 1 \\ -1 & & & \\ & -1 & & \\ \end{pmatrix} = \begin{pmatrix} & & & -1 \\ & & 1 & \\ & 1 & & \\ -1 & & & \\ \end{pmatrix}$}

{$\begin{pmatrix} 1 & & & \\ & -1 & & \\ & & 1 & \\ & & & -1 \\ \end{pmatrix} \begin{pmatrix} & & 1 & \\ & & & 1 \\ -1 & & & \\ & -1 & & \\ \end{pmatrix} = \begin{pmatrix} & & 1 & \\ & & & -1 \\ -1 & & & \\ & 1 & & \\ \end{pmatrix} = j = J_2$}

{$\begin{pmatrix} & 1 & & \\ 1 & & & \\ & & & 1 \\ & & 1 & \\ \end{pmatrix} \begin{pmatrix} & & 1 & \\ & & & 1 \\ -1 & & & \\ & -1 & & \\ \end{pmatrix} = \begin{pmatrix} & & & 1 \\ & & 1 & \\ & -1 & & \\ -1 & & & \\ \end{pmatrix} = k$}

Thus the {$2\times 2$} matrices {$M_l$} are mapped by {$L_4$} to an isometry that involves multiplying by {$M_l$} in one direction and {$-M_l$} in the opposite direction.

{$\mathbb{C}$}

{$I=1$}	{$J_1=i$}
{$\begin{pmatrix} 1 & \\ & 1 \\ \end{pmatrix}$}	{$\begin{pmatrix} & -1 \\ 1 & \\ \end{pmatrix}$}

{$\mathbb{H}$}

{$I=1$}	{$J_1=i$}	{$J_2=j$}	{$J_1J_2=ij$}
{$\begin{pmatrix} 1 & & & \\ & 1 & & \\ & & 1 & \\ & & & 1 \\ \end{pmatrix}$}	{$\begin{pmatrix} & -1 & & \\ 1 & & & \\ & & & -1 \\ & & 1 & \\ \end{pmatrix}$}	{$\begin{pmatrix} & & 1 & \\ & & & -1 \\-1 & & & \\ & 1 & & \\ \end{pmatrix}$}	{$\begin{pmatrix} & & & 1 \\ & & 1 & \\ & -1 & & \\ -1 & & & \\ \end{pmatrix}$}

{$\mathbb{H}\oplus\mathbb{H}$}

{$\begin{pmatrix} 1 & & & & & & & \\ & 1 & & & & & & \\ & & 1 & & & & & \\ & & & 1 & & & & \\ & & & & 1 & & & \\ & & & & & 1 & & \\ & & & & & & 1 & \\ & & & & & & & 1 \\ \end{pmatrix}$}	{$\begin{pmatrix} & -1 & & & & & & \\ 1 & & & & & & & \\ & & & -1 & & & & \\ & & 1 & & & & & \\ & & & & & -1 & & \\ & & & & 1 & & & \\ & & & & & & & -1 \\ & & & & & & 1 & \\ \end{pmatrix}$}	{$\begin{pmatrix} & & 1 & & & & & \\ & & & -1 & & & & \\ -1 & & & & & & & \\ & 1 & & & & & & \\ & & & & & & 1 & \\ & & & & & & & -1 \\ & & & & -1 & & & \\ & & & & & 1 & & \\ \end{pmatrix}$}	{$\begin{pmatrix} & & & -1 & & & & \\ & & -1 & & & & & \\ & 1 & & & & & & \\ 1 & & & & & & & \\ & & & & & & & 1 \\ & & & & & & 1 & \\ & & & & & -1 & & \\ & & & & -1 & & & \\ \end{pmatrix}$}
{$I=1$}	{$J_1=i$}	{$J_2=j$}	{$J_3=J_2^{-1}J_1^{-1}K$}
{$\begin{pmatrix} 1 & \\ & 1 \\ \end{pmatrix}$}	{$\begin{pmatrix} i & \\ & i \\ \end{pmatrix}$}	{$\begin{pmatrix} j & \\ & j \\ \end{pmatrix}$}	{$\begin{pmatrix} -k & \\ & k \\ \end{pmatrix}$}

{$\begin{pmatrix} & & & 1 & & & & \\ & & 1 & & & & & \\ & -1 & & & & & & \\ -1 & & & & & & & \\ & & & & & & & 1 \\ & & & & & & 1 & \\ & & & & & -1 & & \\ & & & & -1 & & & \\ \end{pmatrix}$}	{$\begin{pmatrix} & & 1 & & & & & \\ & & & -1 & & & & \\ -1 & & & & & & & \\ & 1 & & & & & & \\ & & & & & & 1 & \\ & & & & & & & -1 \\ & & & & -1 & & & \\ & & & & & 1 & & \\ \end{pmatrix}$}	{$\begin{pmatrix} & & 1 & & & & & \\ & -1 & & & & & & \\ & & & & 1 & & & \\ & & & -1 & & & & \\ & & & & & 1 & & \\ & & & & -1 & & & \\ & & & & & & & 1 \\ & & & & & & -1 & \\ \end{pmatrix}$}	{$\begin{pmatrix} 1 & & & & & & & \\ & 1 & & & & & & \\ & & 1 & & & & & \\ & & & 1 & & & & \\ & & & & -1 & & & \\ & & & & & -1 & & \\ & & & & & & -1 & \\ & & & & & & & -1 \\ \end{pmatrix}$}
{$J_1J_2$}	{$J_1J_3=J_2K$}	{$J_2J_3=-J_1K$}	pseudoscalar {$J_1J_2J_3=K$}
{$\begin{pmatrix} k & \\ & k \\ \end{pmatrix}$}	{$\begin{pmatrix} j & \\ & -j \\ \end{pmatrix}$}	{$\begin{pmatrix} -i & \\ & i \\ \end{pmatrix}$}	{$\begin{pmatrix} 1 & \\ & -1 \\ \end{pmatrix}$}

Relate {$L$} in various dimensions with the division super algebras and their markers {$e$}.

Louis Kauffman. From Hamilton's Quaternions to Graves and Cayley's Octonions

Octonions take us through the Looking Glass {$L$}.

{$LL=-I$}
{$La=-aL$}
{$(La)(Lb)=Lba$}
{$(La)b=L(ba)$}
{$a(Lb)=L(ba)$}

This yields nonassociativity (based on the "subtractiveness" of the mirror)

{$(Lb)a=L(ab)$} but in general {$L(ab)\neq L(ba)$} because of noncommutativity {$ab\neq ba$}

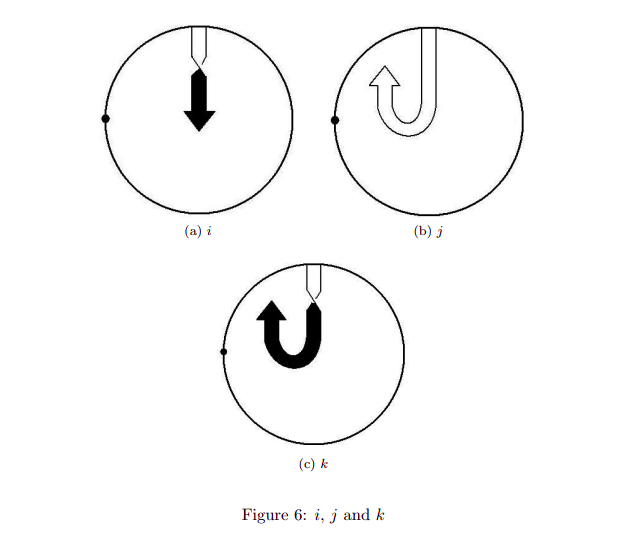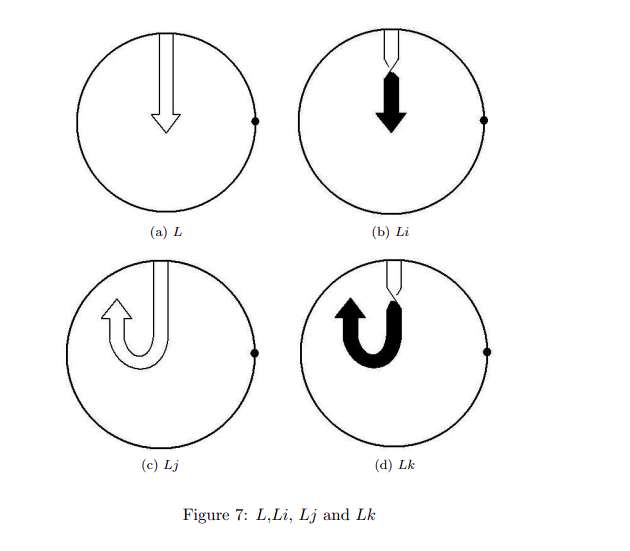Hackett, Kauffman described the belt trick for the octonions where {$L$} plays the role of a context switch or a mirror. They imagine it as a sphere around the belt trick. You can rotate the sphere 180 degrees whereas the quaternions turn at the base.

John Baez. The Octonions. The Fano plane.

The Octonions form seven copies of the quaternions, one for each copy of the circle in the Fano projective plane.

3 of the form {$j(Li)=Lk, (Li)(Lk)=j, (Lk)j=Li$} outer edges of triangle
3 of the form {$L(jL)=j, (jL)j=L,j(L)=jL$} across the center
1 of the form {$ij=k,jk=i,ki=j$} inner circle
what is missing is a line relating the three corners of the triangle {$Li,Lj,Lk$}. Their product is {$L$}.

Further calculations

Define {$A_i=J_i^{-1}J_{i+1}$}.

{$A_i^2=-I$} because {$J_i^{-1}J_{i+1}J_i^{-1}J_{i+1}=-1$}
{$A_i$} is an orthogonal matrix because {$J_i$} and {$J_{i+1}$} are.
{$A_i$} is a skew-symmetric matrix because it is orthogonal {$A_iA_i^T=I$} and {$AA=-I$} means {$A^T=-A$}.
{$A_i$} anticommutes with {$J_i$} but commutes with {$J_1,J_2,\dots,J_{i-1}$}.

Then for {$\gamma(t)=J_ie^{A_i\pi t}=J_i\cos \pi t + J_{i+1}\sin \pi t$} we have {$\gamma (0)=J_i, \gamma(\frac{1}{2})=J_{i+1},\gamma{1}=-J_i$} and {$\gamma(t)$} is a geodesic in {$G_{i-1}/G_i$}.

Think of {$A_i$} as a shift in perspective. Note that {$A_3=-J_3J_4$} and {$A_7=-J_6J_7$} are isometries between eigenspaces {$V_+$} and {$V_-$}.

{$J_1=\textrm{diag}[\begin{pmatrix} & -\hat{I} \\ \hat{I} & \\ \end{pmatrix}]$}	{$A_1=\textrm{diag}[\begin{pmatrix} & & & -\hat{ir} \\ & & -\hat{ir} & \\ & \hat{ir} & & \\ \hat{ir} & & & \\ \end{pmatrix}]$}
{$J_2=\textrm{diag}[\begin{pmatrix} & & \hat{I} & \\ & & & -\hat{I} \\ -\hat{I} & & & \\ & \hat{I} & & \\ \end{pmatrix}]$}	{$A_2=\textrm{diag}[\begin{pmatrix} & -\hat{r} \\ \hat{r} & \\ \end{pmatrix},\begin{pmatrix} & -\hat{r} \\ \hat{r} & \\ \end{pmatrix},-\begin{pmatrix} & -\hat{r} \\ \hat{r} & \\ \end{pmatrix},-\begin{pmatrix} & -\hat{r} \\ \hat{r} & \\ \end{pmatrix}]$}
	{$A_3=\textrm{diag}[\begin{pmatrix} & -\hat{I_8} \\ \hat{I_8} & \\ \end{pmatrix}]$}
	{$A_4=\textrm{diag}[\begin{pmatrix} & \hat{ir} \\ -\hat{ir} & \\ \end{pmatrix}]$}
	{$A_5=\textrm{diag}[\begin{pmatrix} & & & -\hat{I} \\ & & \hat{I} & \\ & \hat{I} & & \\ -\hat{I} & & & \\ \end{pmatrix}]$}
	{$A_6=\textrm{diag}[\begin{pmatrix} & -\hat{r} \\ \hat{r} & \\ \end{pmatrix}]$}
	{$A_7=\textrm{diag}[-\hat{i}]$}