Introduction E9F5FC

Questions FFFFC0

• View
• Edit
• History
• Print

Clifford algebras, Clifford modules

Bott Clock for Clifford Algebras

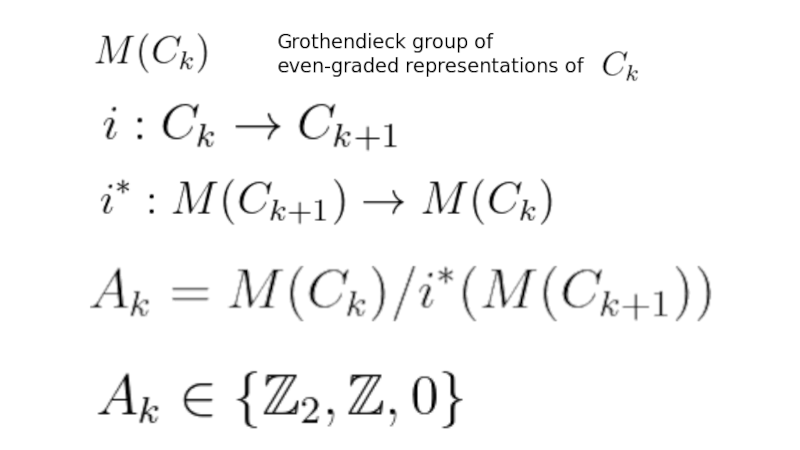
{$A_1$}

{$\mathbb{C}=Cl_{0,1}$} and {$\mathbb{H}=Cl_{0,2}$}

Inclusion by adding a generator {$i:Cl_{0,1}\rightarrow Cl_{0,2}$}

A {$\mathbb{Z}_2$}-graded module of a Clifford algebra is also a {$\mathbb{Z}_2$}-graded module of its Clifford subalgebra where we ignore one generator. {$i^*:M(Cl_{0,2})\rightarrow M(Cl_{0,1})$}

For {$\mathbb{H}$} we have

{$a + be_1e_2 + ce_1 + de_2\Leftrightarrow \begin{pmatrix} a & -b & -c & -d \\ b & a & d & c \\ c & -d & a & -b \\ d & -c & b & a \end{pmatrix}$}

Set {$b=d=0$}. We get

{$a + ce_1 \Leftrightarrow \begin{pmatrix} a & 0 & -c & 0 \\ 0 & a & 0 & c \\ c & 0 & a & 0 \\ 0 & -c & 0 & a \end{pmatrix}$}

which is isomorphic to

{$\begin{pmatrix} a & -c & 0 & 0 \\ c & a & 0 & 0 \\ 0 & 0 & a & c \\ 0 & 0 & -c & a \end{pmatrix}$}

which is two copies of the simple {$\mathbb{Z}_2$}-graded module for {$C$}. Thus the simple module {$\mathbb{Z}_2$}-graded module for {$H$} is mapped to two copies to the simple module for {$C$}. And if we consider all of the simple modules for {$H$}, they are multiples of the unique simple module. So these are mapped to all multiples of two copies of simple modules for {$C$}.

Thus we get {$\mathbb{Z}/2\mathbb{Z}\cong \mathbb{Z}_2$}.

{$A_2$}

{$\mathbb{H}=Cl_{0,2}$} and {$\mathbb{H}\oplus\mathbb{H}=Cl_{0,3}$}

For {$\mathbb{H}\oplus\mathbb{H}=Cl_{0,3}$} we have

{$a + be_1e_2 + ce_2e_3 + de_1e_3 + ee_1 + fe_2 + ge_3 + he_1e_2e_3 = $}

{$a + bk + c(-j\omega) + d(i\omega) + ei + fj + g(k\omega) + h(-\omega)$}

{$\Leftrightarrow \begin{pmatrix} a & b & c & d & e & f & g & h \\ -b & a & d & -c & f & -e & -h & g \\ -c & -d & a & -b & -g & h & e & -f \\ -d & c & b & a & -h & -g & f & e \\ -e & -f & g & -h & a & -b & d & c \\ -f & e & h & g & b & a & c & -d \\ -g & -h & -e & -f & -d & -c & a & b \\ h & -g & f & -e & -c & d & -b & a \end{pmatrix}$}

Set {$c=d=g=h=0$}. This gives:

{$\Leftrightarrow \begin{pmatrix} a & b & 0 & 0 & e & f & 0 & 0 \\ -b & a & 0 & 0 & f & -e & 0 & 0 \\ 0 & 0 & a & -b & 0 & 0 & e & -f \\ 0 & 0 & b & a & 0 & 0 & f & e \\ -e & -f & 0 & 0 & a & -b & 0 & 0 \\ -f & e & 0 & 0 & b & a & 0 & 0 \\ 0 & 0 & -e & -f & 0 & 0 & a & b \\ 0 & 0 & f & -e & 0 & 0 & -b & a \end{pmatrix}$}

which is isomorphic to

{$\Leftrightarrow \begin{pmatrix} a & b & e & f & 0 & 0 & 0 & 0 \\ -b & a & f & -e & 0 & 0 & 0 & 0 \\ -e & -f & a & -b & 0 & 0 & 0 & 0 \\ -f & e & b & a & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & a & -b & e & -f \\ 0 & 0 & 0 & 0 & b & a & f & e \\ 0 & 0 & 0 & 0 & -e & -f & a & b \\ 0 & 0 & 0 & 0 & f & -e & -b & a \end{pmatrix}$}

which is two copies of the module for {$\mathbb{H}$} (?)