Math 4 Wisdom. "Mathematics for Wisdom" by Andrius Kulikauskas.

Read p. 71-84. Exercises 2, 4.

Exercise 2

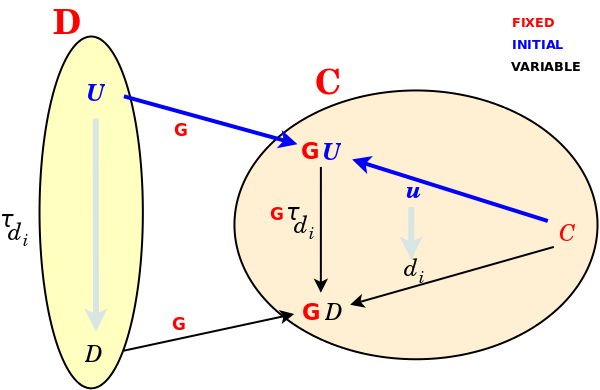
Let {$\Delta :\mathbf{C}\Rightarrow \mathbf{C}\times\mathbf{C}$} bet the diagonal functor, which sends an object {$C$} of {$\mathbf{C}$} to the ordered pair {$(C,C)$} and a morphism {$f:C\rightarrow C'$} to the morphism {$(f,f):(C,C)\rightarrow (C',C')$}. Show that we can view the product as couniversal for this functor.

The statement that the object {$(S,v:FS\rightarrow D)$} is terminal in the comma category {$(F\rightarrow D)$} is the following:

Couniversal mapping property (CMP): For every {$f:FC\rightarrow D$}, there is a unique {$\mu_f :C\rightarrow S$} for which

{$f=v\circ F_{\mu_j}$}

In this case, the pair

{$\nu =(S,v :FS\rightarrow C)$}

is a couniversal pair for {$(D,F)$}, the object {$S$} is the couniversal object, the morphism {$v$} is the couniversal morphism and {$\mu_j$} is the mediating morphism for {$f$}.

For a fixed {$D\in\mathbf{D}$}, the map

{$\mu_{C,D}:\textrm{hom}_D(FC,D)\rightarrow\textrm{hom}\mathbf{C}(C,S)$}

that sends each {$f:FC\rightarrow D$} to its unique mediating morphism {$\mu_f:\mathbf{C}\rightarrow S$} is called the comediating-morphism map for the pair {$(D,C)$} with respect to the couniversal pair {$\nu$}.

Exercise 4

Let {$G$} be a group and let {$R$} be a commutative ring with identity. The group ring {$RG$} is the {$R$}-algebra of formal finite sums {$\sum r_i g_i$}, where {$r_i\in R$} and {$g_i\in G$}. Multiplication is done using the product in {$G$} and linearity over {$R$}. Show that {$RG$} is a universal object.