• View
• Edit
• History
• Print

Research Program

Today I will tell you about the threesome, which is the three-cycle of taking a stand, following through and reflecting. You're probably familiar with it as the scientific method of stating a hypothesis, conducting an experiment and considering the results. In general, this is the mental framework for participation, and in particular, for learning. Thus I may sometimes call it the learning cycle. In math, it shows up in the zig-zag lemma, which is a cornerstone of homological algebra by which a long exact sequence of homology groups is constructed from a short exact sequence of chain complexes. It also shows up in the Jacobi identity for Lie algebras. In such situations, I am curious what kind of learning the threesome, the learning cycle, is modeling?

Initial examples

Definitions

• In terms of ever more fundamental concepts
• Axioms are conditional. What is unconditional?
• Holistic way of looking - consider math holistically

Example: One-all-many

• One-all-many based on constancy

Other representations

• Necessary, actual, possible - logic - truth is "obvious", trivial (as mathematicians say)
• Object, process (morphism), subject - category theory (missing subject)
• One, many, all
• Being, doing, thinking - group theory (action)

In fact, all of the arrows in this diagram correspond to some hidden context involving people: the prediction is dependent on who analyzes the hypothesis, the specification of an experiment is dependent on who is motivated to specify it, and experiments may result in different observations by different observers. ... By choosing a monad we can make explicit (and then hide from discourse) our implicit assumption that “of course this is all dependent on which human is doing the science”. (David Spivak, Category Theory for Scientists (old version), pg.242.)

12 categories

• Kant's categories - why they differ
• Kant's categories - logical form (A -> B) - much like category theory
• perhaps related: Gian-Carlo Rota's twelvefold way counting f:X balls -> Y boxes - but will consider the three columns (any f, injective (balls in separate boxes), surjective (all the boxes have balls) - and the four rows are (distinguishable vs. indistinguishable (equal up to a permutation)) x (boxes vs. balls). Relate to divisions. Compare with one-all-many and then the other representations. Which is human or divine - distinguishable or indistinguishable?
  • Consider instead the category of pointed sets. It has zero objects (pointed singletons). It is equivalent to the category of sets and partial functions. It supports adjoint seven-tuple from the constant functor from C to its arrow category. (Whereas the Yoneda embedding and homsets ground a special role for the Set category.) Pointed set relates to the Axiom of Choice.
• Mind games
• Vocabulary of the imagination
• Example of conceptions - representations

Deeper example: Three-cycle

• Even deeper: three-cycle because based on self-relationship.
  • Where is the constancy? In taking a stand (one), following through (all), reflecting (many).

How I came upon it at the University of Chicago. What is happiness?

Philosophy

• Scientific method
• Sesame street
• Army action review

Roger Penrose His book "The Road to Reality" is a thousand page survey the mathematics used in physics. He has made it available online for free. He begins with a self-analysis of his prejudices that he encapsulates in this picture.

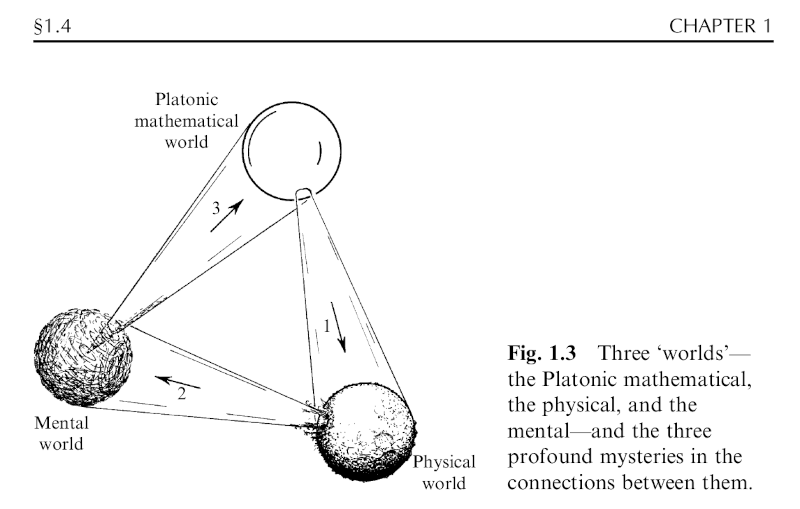
mathematical laws, actions of the universe, the scope of reason

• "everything in the physical universe is indeed governed in completely precise detail by mathematical principles"
• "all of mentality has its roots in physicality"
• "there are no mathematical truths that are beyond the scope of reason"

He concludes, "How can it be that, in accordance with my own prejudices, each world appears to encompass the next one in its entirety? I do not regard this issue as a reason for abandoning my prejudices, but merely for demonstrating the presence of an even deeper mystery that transcends those which I have been pointing to above."

What more could he do with these ideas? Who could he talk with about them? The goal of Math 4 Wisdom is to present and develop ways to meaningful approach such ideas.

He tried to connect them with Plato's values of truth, beauty and good. There was not clear connection. However, we can assert one with the scientific method.

The hypothesis is formulated in the mathematical world, the experiment takes place in the physical world, the observation is perceived in the mental world.

Scientific method basis for agreement

• Prophet Daniel - eating vegetables
• Jesus: judge the tree by the fruit - otherwise sin against the Holy Spirit
• McMaster Institute leader change of mind
• judge my ideas by their fruits - that is why I'm focusing on math
• mathematicians and physicists have blindspots

Note that others consider the scientific method to have more steps.

• Repeats twice: "analyzed by a person yields", "analyzed by a person produces"
• Three are actually relevant: "When, in an experiment, the observation matches the hypothesis—success!—that is agreement." Spivak, Category Theory for Scientists (free version) pg.7 Note that here he conveys the entire sense with only three terms: hypothesis, experiment, observation. And we see that hypothesis is stating before the experiment and observation is stating after the experiment. Experiment is as if the tensor product of the other two.

David Spivak. Categorical interaction in the polynomial ecosystem.

Khan Academy. The Science of Biology The scientific method has five basic steps, plus one feedback step:

• Make an observation.
• Ask a question.
• Form a hypothesis, or testable explanation.
• Make a prediction based on the hypothesis.
• Test the prediction.
• Iterate: use the results to make new hypotheses or predictions.

Wikipedia: Scientific Method describes a four step or six step process.

• diagram

Double loop learning

• Working to uncover a language of truth for deep agreement.
• Uncover the deep structures and then explain the variants that arise.
• Math can help provide a status of a deeper truth

Give math examples:

• SU(2) - Pauli matrices, quaternions
• Triangulation - learning about a surface - not reversible
• Cross product - learning the surface ?
• Jacobi identity - Lie algebra is learning the Lie group
• ABC=CAB linear Turing machine - tangential
• Curry-Howard-Lambek programming languages, type theory, category theory (directionality unclear)(and also considered as a tetralogy)(but note eight levels of logic)
• Long exact sequence - derived functors, learnability - injective resolutions (exhibits directionality)
  • explain relation to the existence of holes, what is not
• Compare with injective - any - surjective function in Stanley's twelvefold way, and try to give examples of short exact sequences.
• Fiber sequences, Fiber bundle, Mapping cone (cofiber)
• F → E → B (take a stand -> follow through -> reflect) examples: cylinder (exact), Moebius strip (not exact for line segment - get leftover space - so use double line segment).
• {$\cdots\to\pi_n(F)\to\pi_n(E)\to\pi_n(B)\to\pi_{n-1}(F)\to\cdots \to \pi_{0}(F) \to \pi_{0}(E)$}
• "the long exact sequence of homotopy groups follows from the fact that the homotopy groups can be obtained as suspensions, or dually, loop spaces."
• Puppe sequence
• Triangulated category and, in particular, Derived category But some experts suspect that triangulated categories are not really the "correct" concept.
  • Wisdom is a guide for deep mathematical insights. Pythagoras, Descartes, Pascal, Leibniz, Frege, Whitehead. And if a philosopher's insights aren't providing mathematical insight, then in what sense is their thinking sound, solid, applicable, verifiable, fruitful? Or perhaps they are providing metaphysical insight, then let us show where and how that expresses itself in mathematics. Metaphysics is conceptual mechanics - where by concepts not meaning so much the formal sense but moreso the issues they refer to.
• four ways of looking at a triangle - four geometries
• Goedel's theorem - and a three-cycle as a state which can be contradictory yet inhabitable

Accountability

• Practical example: Who caused the Holocaust in Lithuania?
• Practical example: Who is causing climate change?