• View
• Edit
• History
• Print

Research Program

Foursome

• Another example: foursome
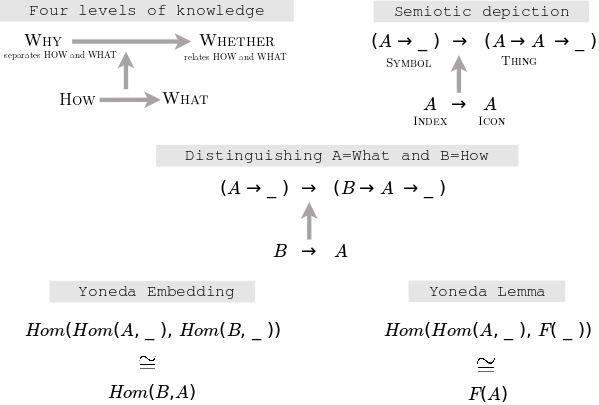
  • Levels of knowledge.
  • Example: the bottle
  • Plato, Aristotle
  • Idealism vs. materialism
• Peirce's signs
  • progression in evolution
  • natural transformations distinguish - icon, index
  • thing - identity morphism = object (object is what has an identity morphism - whether it is an object)
  • symbols - absolutely any relationship
• Yoneda Lemma, embedding
  • functions like knowledge switch

Consider also the case where F is the identity I, and thus A is a set. Look at the natural isomorphism.

• global quantum - Maxwell's demon operates the knowledge switch - Bible story - how physicists talk about the global quantum - that you run out of tape - Rolf Landauer - but they don't specify the cut off
• automata theory Chomsky hierarchy.

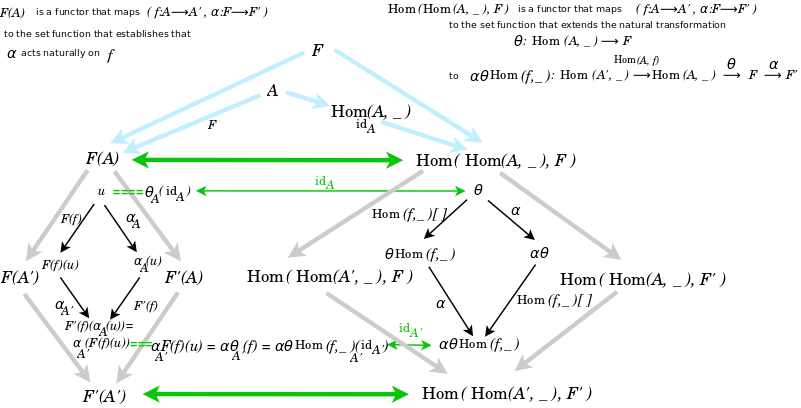
In his comment at Math Stack Exchange, Nex describes the two functors {$ R $} and {$ L $} thusly:

• {$ R $} is {$ ((α,f):(F,A)→(F′,A′))↦(x↦α_{A′}(F(f)(x))) $} and the objects are mapped {$ (F,A)↦F(A) $}
• {$ L $} is {$ ((α,f):(F,A)→(F′,A′))↦(θ↦(α⋅θ⋅\textrm{Hom}(f,−))) $} and the objects are mapped {$ (F,A)↦\textrm{Nat}(\textrm{Hom}(A,−),F) $}
  • • Consider the distribution of the largest eigenvalue for a random matrix. The peak is at {$\sqrt{2N}$}. The distribution drops as {$e^{-N^2}$} to the left and as {$e^{-N}$} on the right.
    • Finite automata - strong coupling - scale as N^2. Push-down automata - subsystems - weak coupling - scale as N.
    • How could the largest eigenvalue be larger than expected? There are not many ways and thus it drops down quickly. How could it be smaller than expected? There are many more ways, mixing positive and negative, and thus it drops down slowly.
    • Quanta Magazine. Beyond the Bell Curve - A New Universal Law Satya Majumdar, Grégory Schehr. The critical point at √2N separates a stable phase of weakly coupled species, whose populations can fluctuate individually without affecting the rest, from an unstable phase of strongly coupled species, in which fluctuations cascade through the ecosystem and throw it off balance. In general, Majumdar and Schehr believe, systems in the Tracy-Widom universality class exhibit one phase in which all components act in concert and another phase in which the components act alone. The asymmetry of the statistical curve reflects the nature of the two phases. Because of mutual interactions between the components, the energy of the system in the strong-coupling phase on the left is proportional to N2. Meanwhile, in the weak-coupling phase on the right, the energy depends only on the number of individual components, N
    • Universality principle " as the phase transition is approached, the scale-dependent parameters play less and less of an important role, and the scale-invariant parts of the physical description dominate. Thus, a simplified, and often exactly solvable, model can be used to approximate the behaviour of these systems near the critical point. "
  • Two objects cannot be in the same place, and the same is true for fermions. But two arrows can be in the same place, and the same is true for bosons. I mean to say that two arrows can start at the same object and end at the same object but be entirely different arrows. So a shift from an "object point of view" to an "arrow point of view" may be like a shift from "fermion statistics" to "boson statistics".
  • Univalence Axiom {$(A=B)\simeq(A\simeq B)$}
  • Yates index theorem, the jump hierarchy.
    • Unconscious, conscious, consciousness
  • 4 sheave functors
  • Feynman diagrams with 4 fields

Nigel Goldenfeld: Seeing Emergent Physics Behind Evolution

• Condensed matter physics: collective effects. Horizontal gene transfer - network of life - exponential growth. But perhaps this hit a global quanta limit and that is why the cell arose as a subroutine.

Everything

Four properties of everything

• Russell's paradox