Math 4 Wisdom. "Mathematics for Wisdom" by Andrius Kulikauskas.

Andrius Kulikauskas: This is where I jot down my notes. In general, in this Exposition, any grey areas are for my personal notes.

I need to delete, move, organize these notes

Such concepts are typically defined in terms of simpler concepts and yet we neglect to define the simplest concepts.

These are mathematical structures which I am working to interpret as frameworks for how cognitive perspectives fit together.

I have in mind a very particular set of mathematical structures which I believe express cognitive frameworks for wisdom that also serve as keys for making sense of all of abstract math.

Can I provide wonderful insights into mathematics and related subjects? If so, then perhaps you will make an effort to learn my language and make it your own. We can work together to find connections between wisdom and mathematics, to draw insights from mathematics, to express wisdom accurately, to overview the whole of mathematics and make sense of it, and ultimately to apply wisdom in all of life, and foster a shared culture of wisdom. This is why I'm creating Math 4 Wisdom.

What is a perspective?

No perspective (God), perspective (I), perspective upon perspective (You), perspective upon perspective upon perspective (Other).

Category theory - composition
Octonions - nonassociative
Projective geometry
Carving out mental space - thinking holistically.
Bott periodicity

Thinking-in-parallel

Thinking in parallel - the three basic ways

Thinking-in-parallel is a key property of experiencing life and being aware of the thinking-in-parallel which proceeds inside of you is key for your own wisdom.
We can grow aware of thinking-in-parallel by respectfully listening to another's perspective while maintaining one's own independent perspective.
We grow further aware by having internal dialogue.
We grow more aware by studying the nature of that dialogue, how perspectives fit together as cognitive frameworks to flesh out existential issues.
Two-track mind for existence, three-track mind for participation, notably for learning, and a four-track mind for knowledge.
The basics for wisdom - look for them in mathematics.

Abbreviations

"My analysis" ...
"My vocabulary" ...

If it helps to be more sympathetic, you can consider this as my own private language, as science fiction...

More questions of interest

I will keep switching back and forth between mathematics and wisdom so as to maintain interest among those of you who are primarily interested in advanced mathematics and those who may not understand any of it but are very keen to investigate wisdom.

Here are some more subjects in math that are relevant for how perspectives can fit together.

Understanding the Schroedinger equation and quantum field theory in terms of the combinatorics of orthogonal polynomials.
The Chomsky hierarchy in automata theory.
The arithmetic hierarchy in computability theory.
Universality principle, random matrices, in statistics and dynamical systems,
Univalence axiom in homotopy type theory.
Entropy.
Sequences, hierarchies, networks.
Random walks on binary trees.

Goals that relate math and wisdom

Show mathematicians structures to be on the look out for.
Show my philosophy as a work-in-progress that is coming together.

What is wisdom - knowing everything

Wisdom - knowing everything - knowing something or anything about everything - what can we say about how everything is organized?

Mental chambers - arguing various issues
Guide through a mental prison - understanding the limits of the imagination - venture into the mathematical caves.
Relate the language of wisdom and the language of math.
I speak the language of wisdom - I have fluency, as a personal language - I want to convey that - with the help of the language of mathematics - so this research program is a Rosetta stone.
Intuition - extra dimension - depth perception instead of time.
My approach is to observe the limits of my imagination, to document the cognitive frameworks by which I and others live and think, to

math includes ...

By knowing everything, I mean a Godly, perfect, total, complete, absolute knowledge of the vantage point from which everything makes sense, from which we have the big picture. Of course, from the heights of that Olympus my human-sized brain and my nearsighted eyes will not penetrate through all the clouds below, will not engage all the details at once. Therefore by knowing everything, I also mean the further ability to descend into the details, to readily find the answer to any particular question we may have, including any mathematical question, and then to climb back up to that perfect vantage point. Certainly, I would want to be able to explain where all of math comes from, and how it unfolds, all of the branches, concepts, structures, theorems, questions, ideas, challenges, opportunities, in all their possible directions and subdirections. And if I did do that, if I laid out all of mathematics before you, so that you could see with childlike fascination, at every step, the options by which it proceeds, up through the most impossibly profound results, all of the mathematics that there could every possibly be, as if you were exploring a miraculous fractal world, zooming through a Mandelbrot set of ideas, then I would feel comfortable, I would feel emboldened to tell you that my findings about the wisdom of life may likewise be valid. The goal of knowing everything, the proper, useful, beautiful application of that knowledge, is for independent thinkers to foster a community, nurture a science, develop a conceptual language, not just for a map of mathematics but for all of human life, especially that wisdom by which we grow ever more mature, here and now. Math for wisdom is a call around the world to those who are working towards this goal from every imagineable world view. If we want to be sure of exactly what we mean, and be confident that we have uncovered a conceptual language of well formed, well connected and well functioning ideas, and hope that others will trouble themselves to understand, then we should express ourselves in terms of mathematics, or rather, in terms of mathematical ideas, those ideas that mathematics researchers know from their work. Math is the gold standard for utility of expression, which true philosophy should meet, and which sincere poetry admiringly concedes.

Math for Wisdom is my way of engaging you with the topics in advanced mathematics that are relevant for expressing to others the conceptual language that I seek for my own thinking but ultimately for thinking along with you.

In this very first video, I am providing an overview for myself to make clear why and how I personally take up and pull together a variety of mathematical investigations. For my sake and for your sake I believe that I should start with such a straightforward approach. In the future, depending on what you find interesting, I expect to present my investigations in ways that ...

The universal conceptual language that I seek is, like math, an alternative to words. We may use a word like "tree" pragmatically, simply because we want to refer to the chair next to the tree, and so we need not agree as to what we actually mean by tree. If we were to take a tree and make it smaller, then at some point we would surely disagree as to whether it is still a tree or has become a bush. We simply don't need to know or care to know exactly what we mean by tree.

End of Introduction

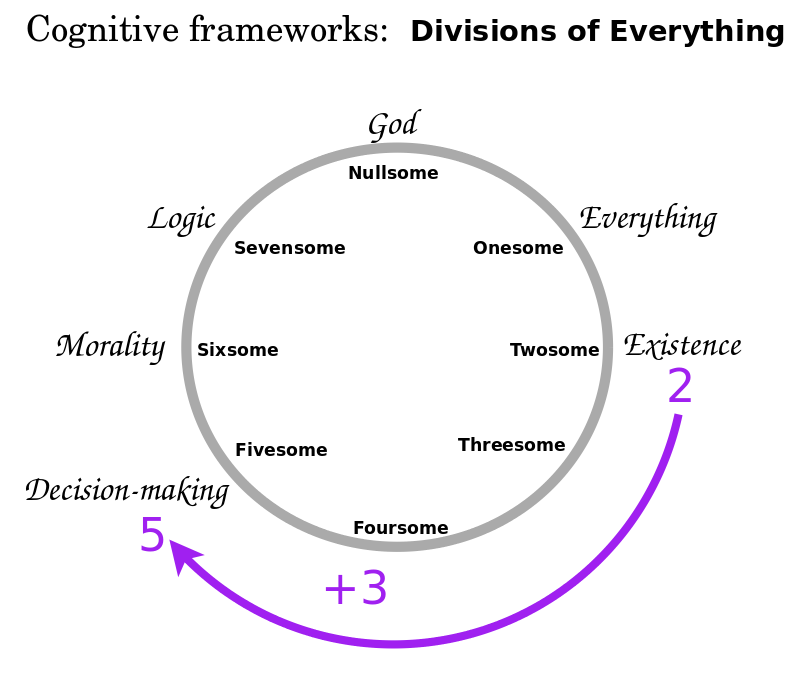
ABC's - twosome, threesome, foursome
See how they come up in more comprehensive and elaborate structures
Consider a more sophisticated structure, the fivesome.

ABC's of Thinking-in-Parallel

3-Track Mind for Learning. Derived functors.

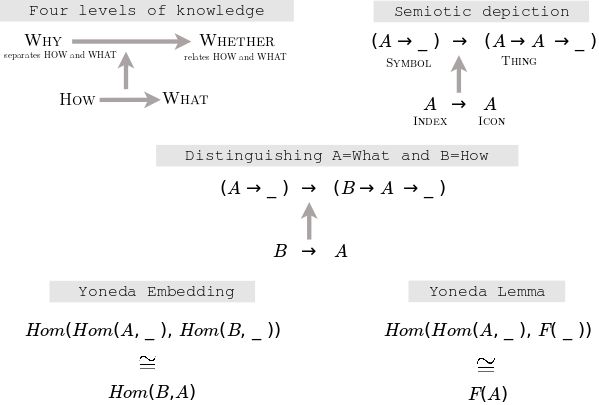
4-Track Mind for Knowledge. Yoneda Lemma.

https://en.m.wikipedia.org/wiki/Grothendieck%27s_relative_point_of_view

Global quantum

Hierarchy problem, dark matter...

2-Track Mind for Existence

Divisions, Conceptions, Circumstances

Six representations

Grothendieck's six operations

The natural bases of the symmetric functions

Hopf algebras.

comultiplication Δ(hk) = 1 ⊗ hk + h1 ⊗ hk−1 + ... + hk−1 ⊗ h1 + hk ⊗ 1.
antipode S(hk) = (−1)k ek

Twelve circumstances

One, all, many

Twelvefold way

Principles of life - Christopher Alexander - Mandelbrot set - Catalan numbers - Dyck words - push down automata.

SU(2) normal form

The cube 8 divisions, 6 conceptions, 12 circumstances.

Divisions - carving mental space

Spin
Exact sequences
Adjunctions

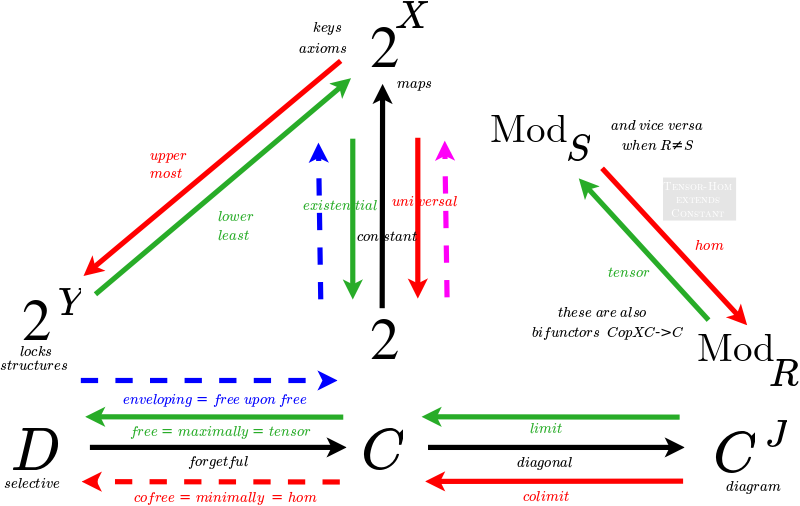
Divisions of everything

Onesome

Division of everything into zero perspectives

4 representations generate nullsome
Foursome negates them
All fits together

More Sophisticated Thinking-in-Parallel

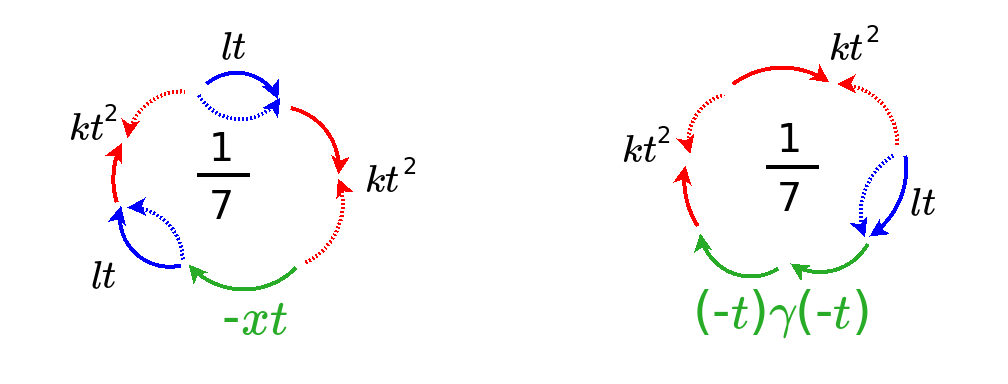
5-Track Mind for Deciding. Dual causality and QFT.

The five conics - Fivesome
Logical connectives - Fivesome
Fivefold classification of Sheffer polynomials of A-type zero - Fivesome

6-Track Mind for Morality. Snake Lemma.

7-Track Mind for Logical System. Logic.
Logical square (and related logic - nonempty (closed) vs. empty (open) system - entropy) - Sevensome-eightsome

Special kind of logic related to Aristotle.

I want to be able to describe the cognitive foundations that account for logic.
Understand the Basics of Logic and Truth. I have made some progress in describing such foundations for truth: Truth as the Admission of Self-

Contradiction. Which is to say, truth is inherently unstable and tentative, the relation of a level with a metalevel.

Shu-Hong's equation for the meaning of probability words in context. {$R=M_p + a^+(C-C_p)$}. Rewritten as {$a^+=\frac{R-M_p}{C-C_p}$}. Where {$R$} is the subject's response (their judgement on the meaning), {$M_p$} is the prototypical meaning, {$C_p$} is the prototypical confidence, {$C$} is the contextual confidence. "The prototypical meaning provides a reference point for the range of meaning, and the range of meaning provides a reference point for confidence, which is compared to the contextual confidence." (pg.143) "Every probability word has a prototypical confidence associated with it." (pg.117) Confidence deals with what we don't know, meaning with what we know?

Mobius transformations. {$f(z) = \frac{a z + b}{c z + d}$}

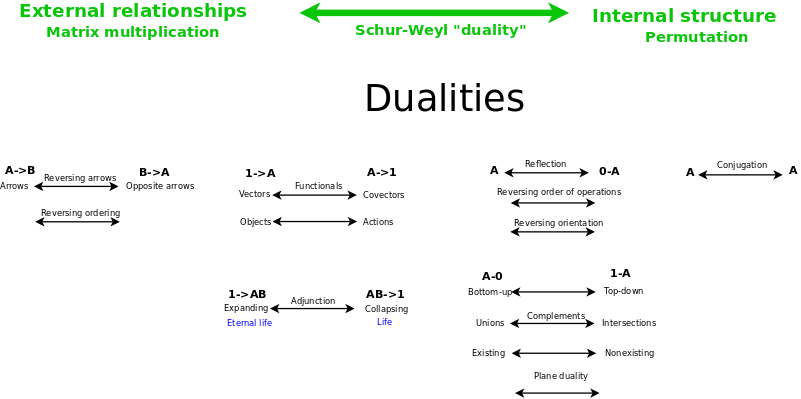
Dualities

Seven-eight kinds of duality. Reps of Sn and GLn. Schur-Weyl duality.

I would like to understand the various kinds of opposites in math and classify them.

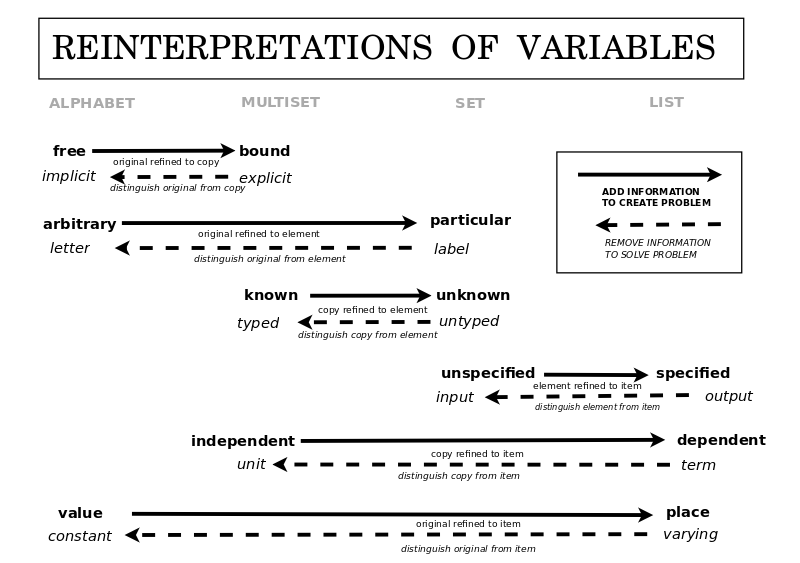
24 Keys For Solving Math Problems

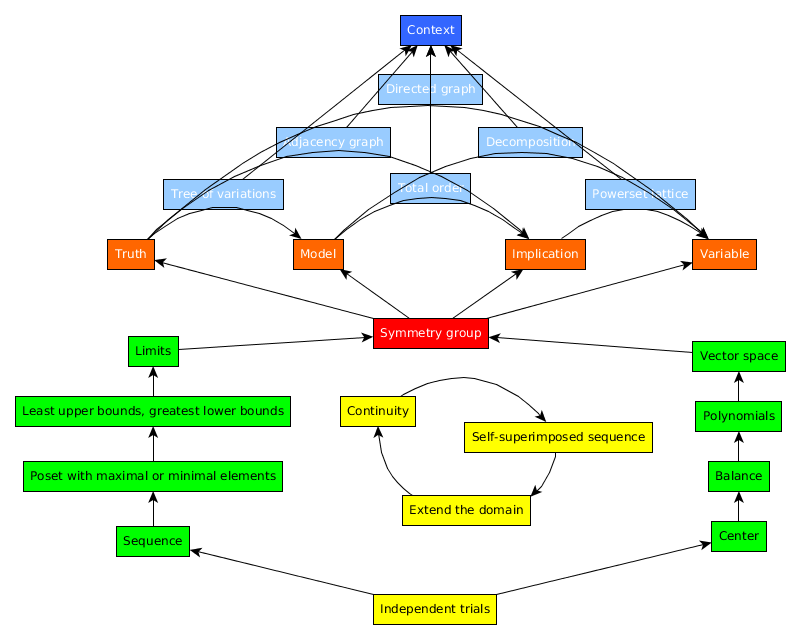
Collecting and analyzing such examples could be a collaborative effort. Here is a database I made of almost 200 examples of figuring things out in math.

I used my philosophical structures to systematize the recurring patterns. This yielded the following diagram. I would like to sharpen the results.

The lower half of the diagram grounds the mathematical thinking which is pre-systemic. The upper half of the diagram grounds that which takes place within a mathematical system.

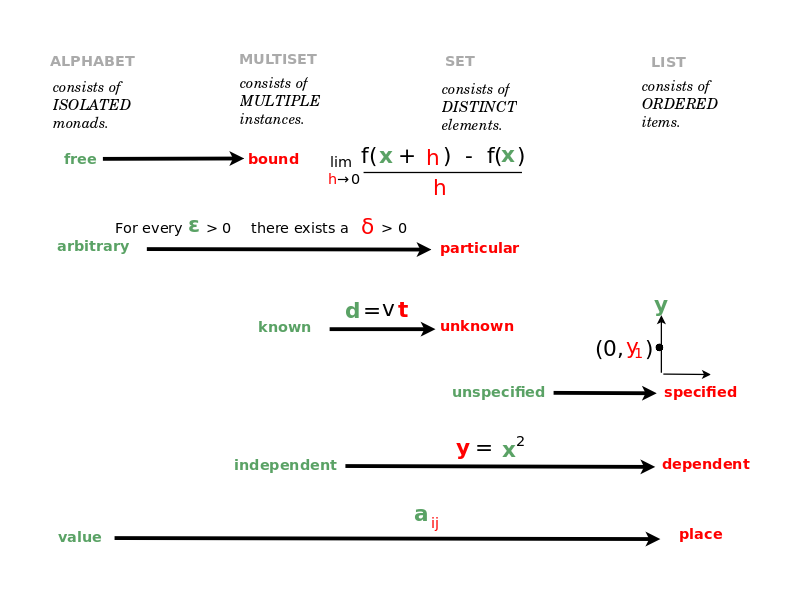
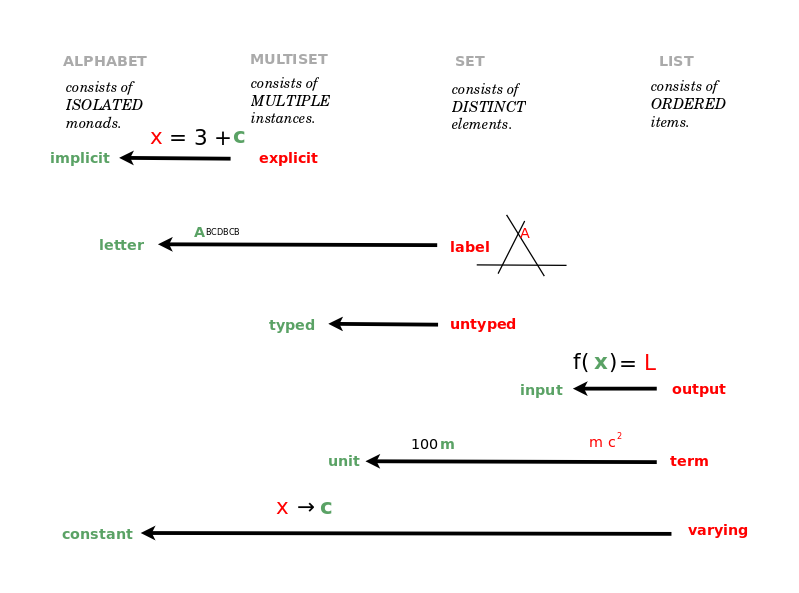
Map of Math: Affine, Projective, Conformal, Symplectic Geometry

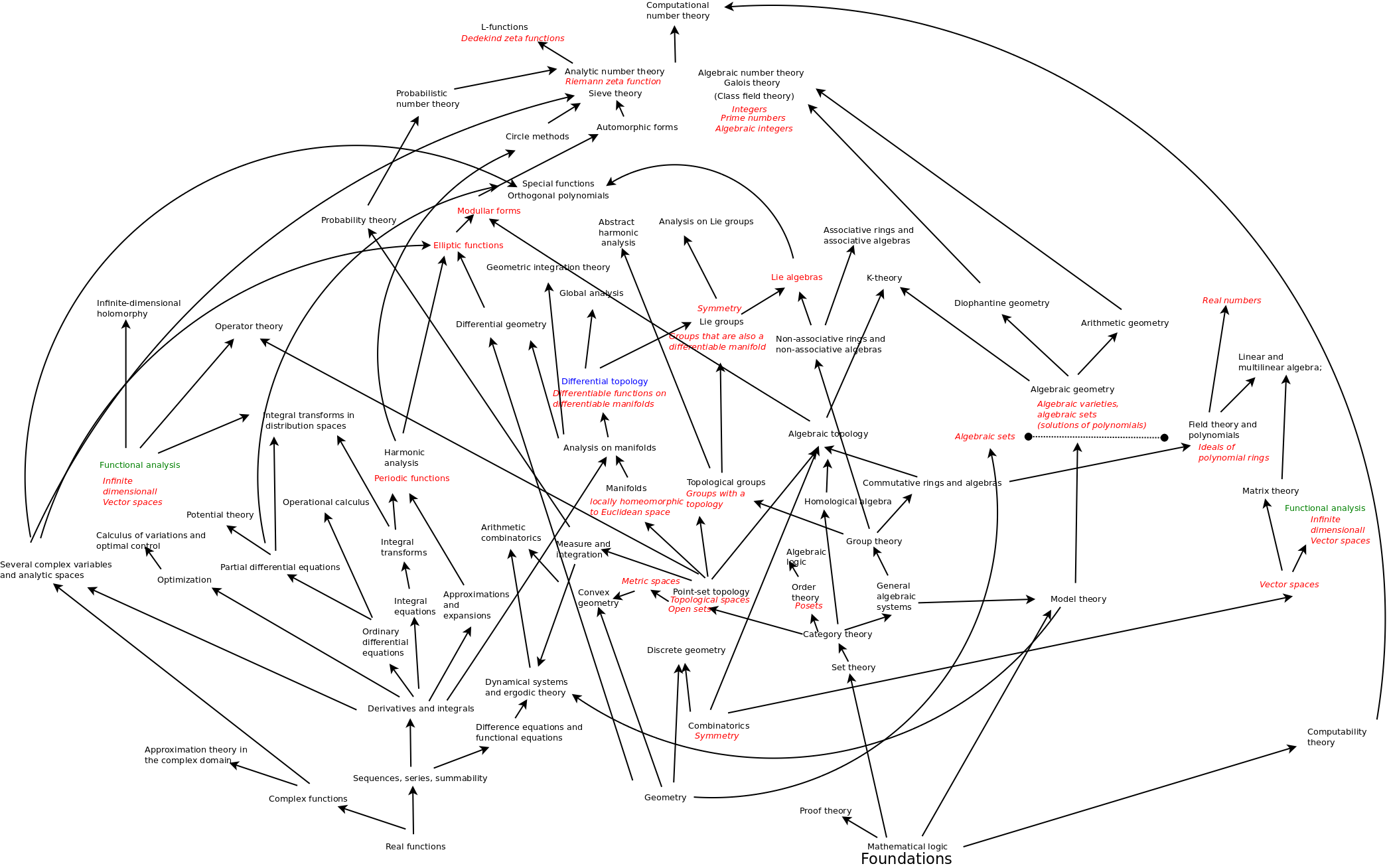
Map of Areas of Mathematics

Based on journal classification
There are two wings, algebra and analysis, related by geometry.
Look at Lie groups-algebras which are at the center and relate the two wings.
Note that they are very concrete and very foundational, ordinary, ubiquitous.
Then look at four classical families.

Algebra and geometry

adjunction: tensor product (geometry) - homset (algebra)
two wings in the house of knowledge
Comparing the price of a sandwich {$\frac{4}{3}\frac{2}{3}=\frac{8}{9}$} as illustrating that algebra is thinking step-by-step.
Geometry as homogeneous space, uniform choices.

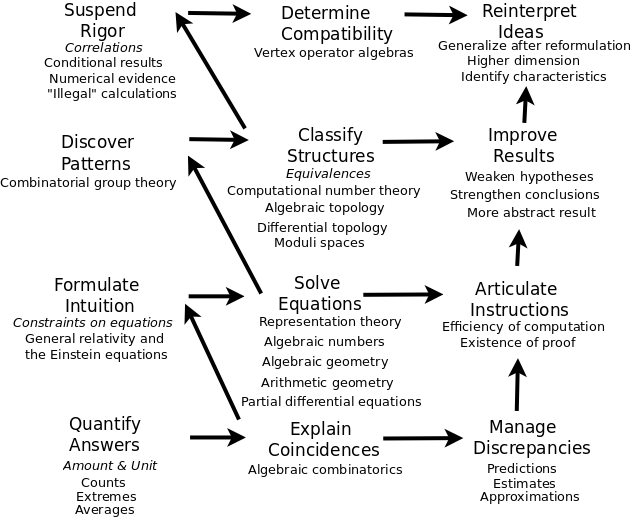
One of my goals is to be able to make a map of how mathematical subjects, concepts and objects become relevant. Such a map would systematize existing mathematics, identify overlooked mathematics, and show the directions in which math can evolve in the future.

I started by organizing the subjects listed in the Mathematics Subject Classification by trying to show which areas depend on which other areas. Acknowledging my general ignorance, I was able to draw several conclusions.

As expected, there do seem to be two major areas, algebra and analysis. The capstone of math seems to be number theory, which makes use of tools from all of math. Lie theory seems especially central as a bridge between algebra and analysis.

Surprisingly for me, geometry seems to be a well spring for math. I studied algebraic combinatorics as "the basement of math" from which I thought mathematical objects arose. Geometry thus seemed rather idiosyncratic. But from the map it seems that geometry is a key ingredient in math, in terms of its content, perhaps in the way that logic is, in terms of its form.

Dualities - note external relationships and internal structures
Dualities - sevensome
Dualities - relate to adjoint string of length seven for pointed sets - carving up the space between geometry and algebra

Yates Index Set Theorem

Arithmetic hierarchy

{$\Pi_1$} Induction {$\forall x P(x)$}
{$\Sigma_2$} Maximum or minimum {$\forall x \exists y (P(x)\Rightarrow P(y))$}
{$\Pi_3$} Least upper bound or greatest lower bound {$\forall x \exists y \forall z ((x \leq y) \wedge (x \leq z \Rightarrow y \leq z))$}
{$\Sigma_4$} Limit {$\forall \delta \exists \epsilon \forall x \exists x_0 (|x-x_0|<\delta \Rightarrow |F(x)-F(x_0)|<\epsilon )$}

Yates Index Set Theorem. (1966) Given r.e. sets C and D such that {$C<_T D$} and {$S\in\Sigma_3^C$} there is a recursive function {$g(k)$} such that for all {$k$}

i) {$D\leq_T W_{g(k)}\leq_T C$}
ii) {$k\in S\Leftrightarrow W_{g(k)}\equiv_T C$}

Corollary (Yates). If C is r.e., then {$\{x:W_x\equiv_T C\}$} is {$\Sigma_3^C$}-complete.

Corollary. The set of indices of Turing complete r.e. sets, Comp = {$x:W_x\equiv_T K$} is {$\Sigma_4$}-complete.

Map based on the Companion

Do the three columns relate to the twelve circumstances? or to the three-cycle in the classification of adjunctions?

Classifying adjunctions and adjoint strings

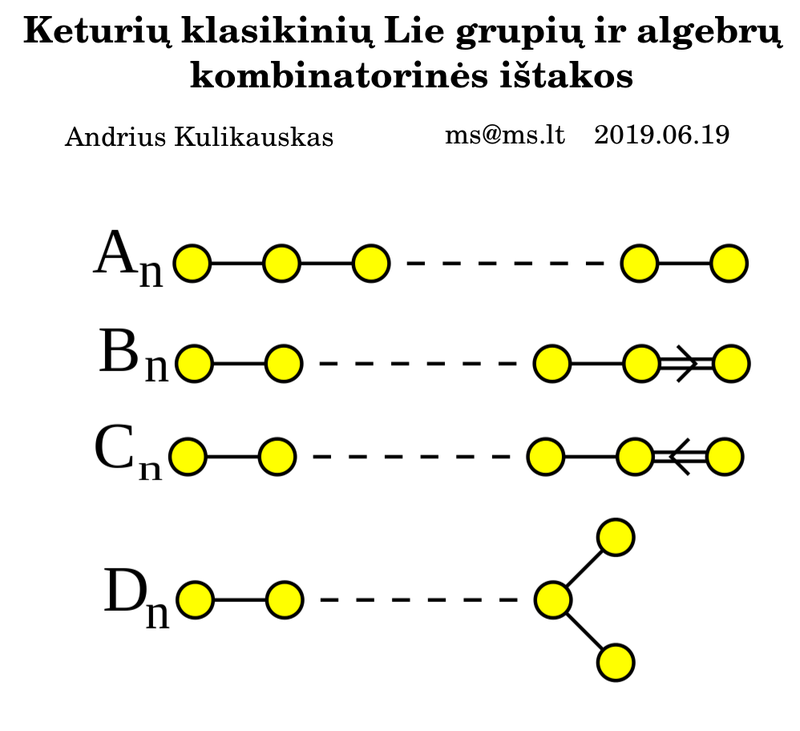
Four classical Lie families - Four levels of geometry and logic

In particular, I am interested in understanding, intuitively, the cognitive foundations for the four classical Lie groups/algebras. I have been learning about the classification through the Dynkin diagrams. But that does not explain intuitively the qualitative distinctions. So instead I have been working backwards, from the Cartan diagrams, trying to understand concretely how to imagine the growth of a chain (how it ever adds a dimension via an angle of 120 degrees) and the possible ways that chain might end.

Polytopes - Choice frameworks

I am encouraged that I myself have made some mathematical discoveries by focusing on these questions. I have thought a lot about the regular polytopes which the Weyl groups are symmetries of.

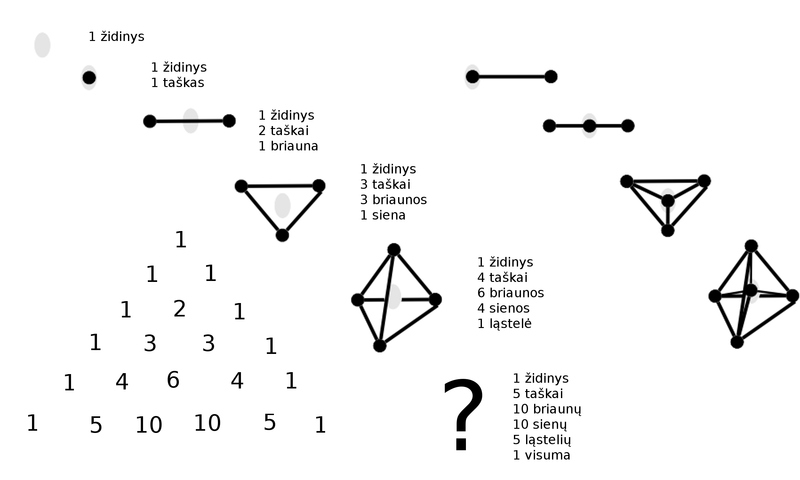
I was able to come up with an interpretation for the -1 simplex and a novel q-analogue of the simplex.

I am also seeing how the polytopes can be thought to a rise by a "center" which ever generates vertices (for simplices), pairs of vertices (for cross-polytopes), planes (for hypercubes) and "coordinate systems". Three infinite families of regular polytopes and an additional family of coordinate systems make for four families of choice frameworks.

In a choice framework, God as center, everything as totality.

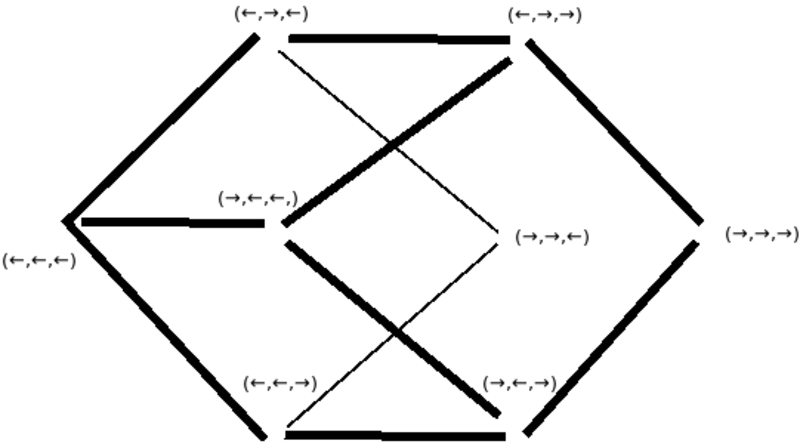
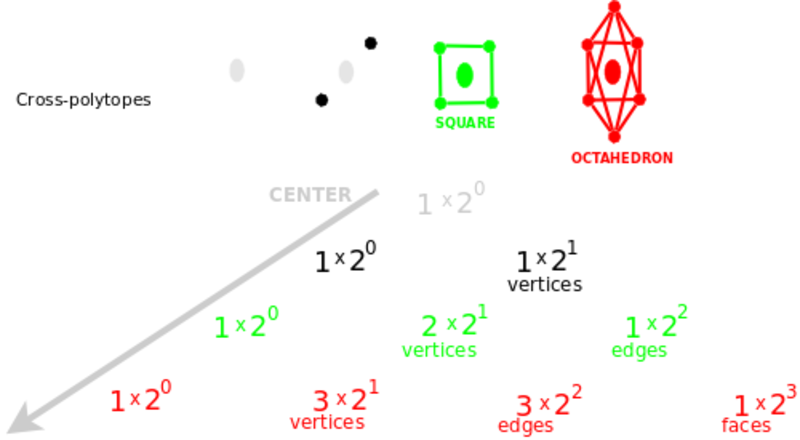
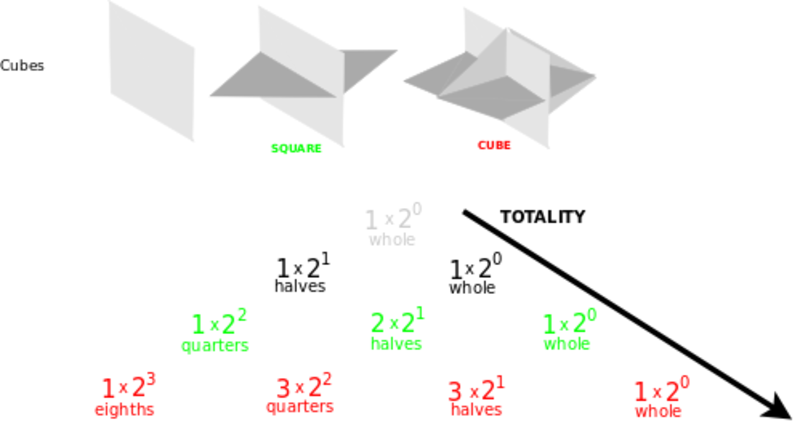
Classical Lie families

Investigation: 4 classical Lie families, 4 geometries, 4 choice frameworks.

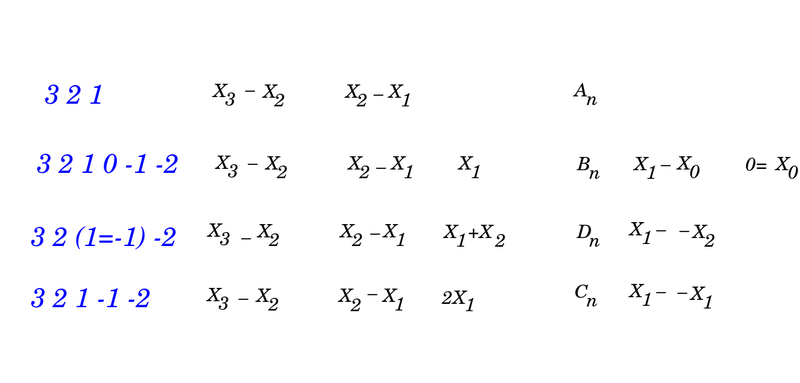
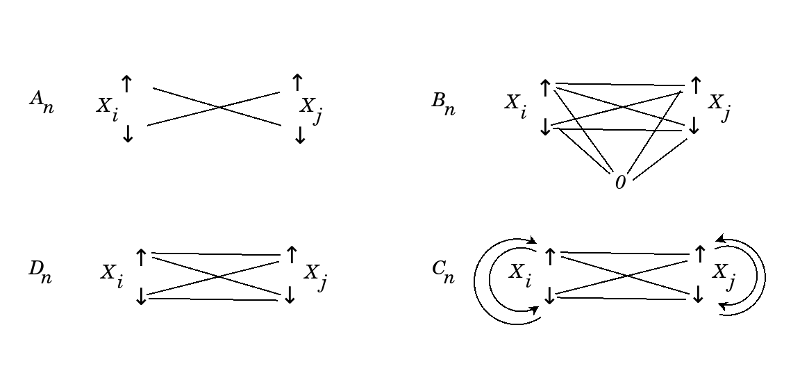
Discover Cognitive Foundations for the Classical Lie Groups/Algebras. It is surprising that in mathematics there is a small collection of structures which seem most rich in content. This is a point that Urs Schreiber keeps returning to. Thus one task is to make a list of such structures and try to relate them with a map, and indeed, understand how they fit in a map of all math.

Four geometries John Baez and others have pointed out that the classical Lie algebras ground different geometries.

Odd orthogonal, even orthogonal (distances, volumes)(orientation), unitary - conformal (angles), symplectic (oriented areas).
I would like to learn the basics of affine, projective, conformal and symplectic geometries so that I could understand how they relate to the four classical groups.

Perspectives

One place to look for the cognitive foundations of mathematics is to develop models of attention, for example, in terms of category theory.

6 visualizations and 6 paradoxes

6 layers in mammalian cortical minicolumns

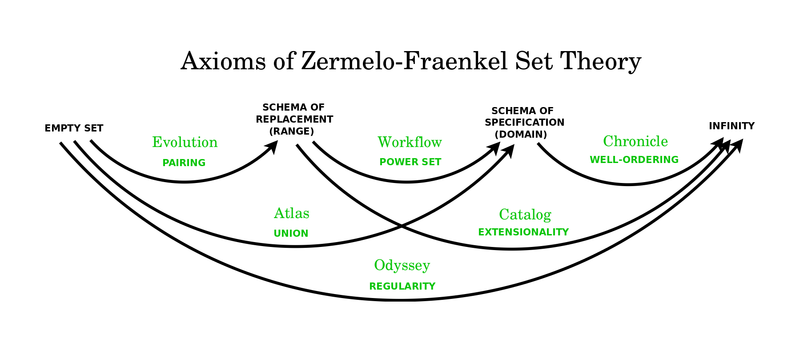
10 axioms of set theory

The axioms of Zermelo Frankel set theory (except for the Axiom of Infinity) and the Axiom of Choice are all present in the above system and so I would like to work further to clarify their role. Of special interest to me, currently, is to study the four concepts (in orange) that seem to ground logic but also geometry. These methods apply the concepts of truth (argument by contradiction), model (solving an easier version), implication (working backwards) and variable (classifying the problem).

4 plus 6 generators of the Poincare group, the symmetries for quantum field theory

Map of Math

Another way to build a map is to use the tags from MathOverflow. The idea is to make a list of the, say, X=100 most popular tags, and also to make a list of the most popular pairs of tags, where pairs are created for any two tags that are used for the same post. In the map, for each popular tag, I would show a link to its most popular pair, and also include, say, the most popular 2X links overall.

Study the Process of Abstraction. Thus it is important to study the process of abstraction. One approach is to try to describe, in an elegant way, a theory that is practically complete, such as the geometry of triangles in the plane. Norman Wildberger's book and videos are very helpful for this. It may be that a matrix approach might be insightful. Having stated a theory it may be possible to see in what directions it develops further.

Another approach is to identify classic theorems in the history of mathematics and consider how abstraction and generalization drove them to arise and develop further.

I would like to learn more about the kinds of equivalences in math - I know that Voevodsky, etc. have studied that deeply - and draw on that and perhaps contribute.

Bott Periodicity: Unfolding of Thinking-in-Parallel

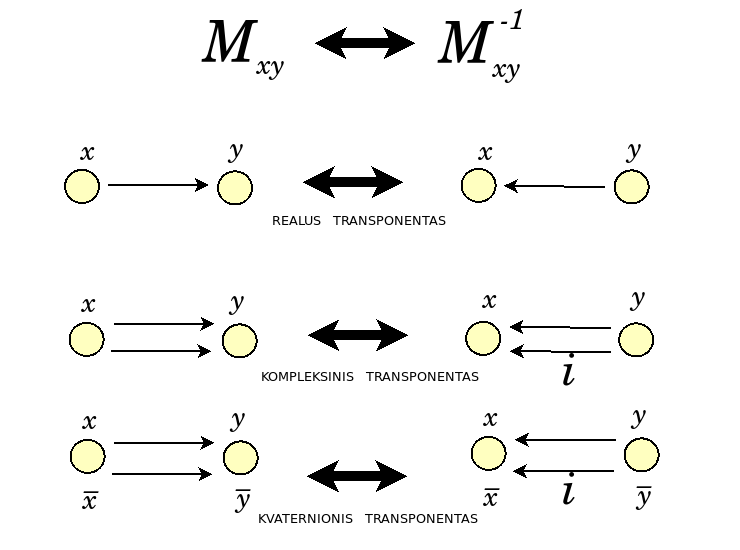
Adjoint string of length N - Division of everything into N perspectives

Exact strings.

Understand intuitively

How could finite exact sequences or perhaps finite strings of adjoint functors model mental chambers, which is to say, holistic cognitive frameworks, divisions of the brain's global workspace, or simply metaphysical divisions of everything?
How could we classify strings of adjoint functors?
How could the eightfold Bott periodicity and/or the classification of real Clifford algebras model how our mind proceeds from one mental chamber to another? Walking through the chambers of the mind.
Why are there four classical families of Lie groups and Lie algebras? and how might they ground four kinds of geometry: affine, projective, conformal, symplectic?
In any system, how could the Poincare group model the relations between such four geometries? And how could we model the additional conditions by which a system comes into being?
How might the degrees of freedom in the gauge theories of the Standard Model

Bott periodicity - Eight-cycle of divisions

Clifford algebras - clock shifts - consciousness

Divisions of everything: Exact Sequences

Divisions of everything: Adjunctions

Exact sequences of length n <=> Divisions of everything into N perspectives

Divisions of everything: Spin

Elementary particles

Higgs - spin 0 - onesome
Matter (leptons, quarks) - spin 1/2 - twosome
Force carrying bosons - spin 1 - threesome
spin 3/2 - not known to exist - foursome (knowledge)
Graviton - spin 2 - fivesome

Divisions of everything: Bott periodicity

Bott Periodicity <=> The eight-cycle of divisions of everything

Operations

Norman Anderson's theory and modeling thinking fast and slow.

Investigating examples of what the operations model.
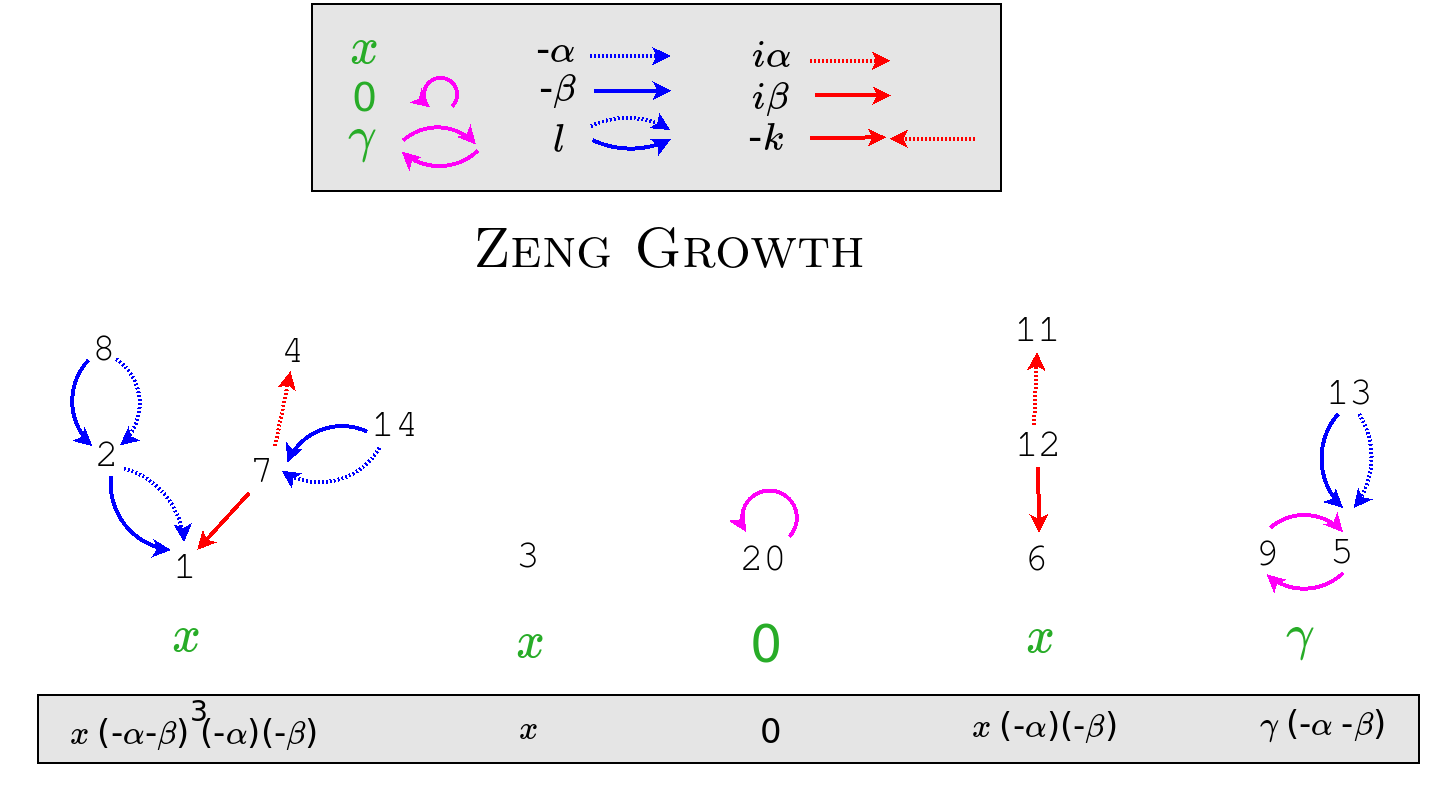
Shu-Hong Zhu and the sevensome

Visualizations - unconscious and conscious

Poincare Group: Organizing Structures and Perspectives

Generation of structures

Not-wishes

{$SU(2)$} - Emotional transformations

Snake lemma

Unclear

Narration

3 Languages

Map of Deepest Values

Antiwishes: Emotional responses: SU(2)

Study the Geometry of Moods

In my study of emotions and moods, I have successfully linked my philosophical and mathematical research. My model of basic emotions is based on whether our expectations are satisfied. Of special importance is the boundary between self and world. For example, if we discover that we are wrong about the world, or anything peripheral, then we may feel surprised, but if we learn that we are wrong about ourselves, or something deeply important, then we may feel distraught. See my talk: A Research Program for a Taxonomy of Moods.

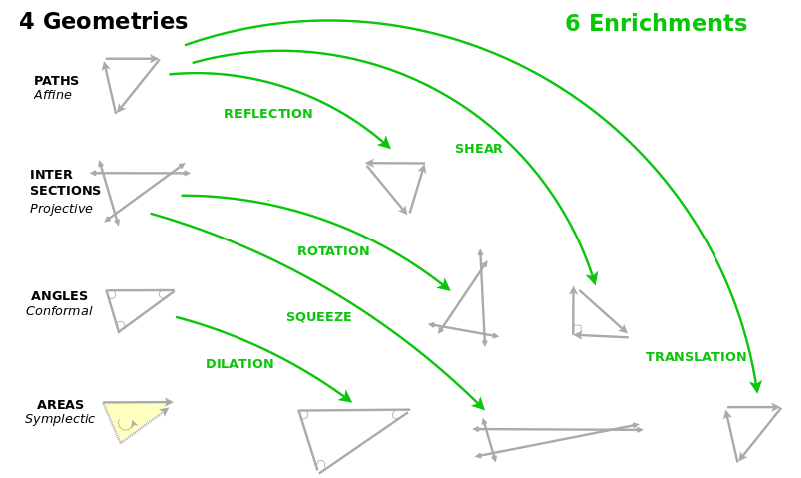
I did a study of some thirty classic Chinese poems from the Tang dynasty to explain the moods they evoked. (In Lithuanian: Nuotaikų aplinkybės: Tang dinastijos poezija ir šiuolaikinė geometrija.) I discovered that the mood depended on how the poem transformed the boundary between self and world. Each of them applied one of six transformations (reflection, shear, rotation, dilation, squeeze, translation) which shifted the geometry from a cognitively simpler one to a cognitively richer one (path geometry - affine, line geometry - projective, angle geometry - conformal, area geometry - symplectic).

20) I would like to better understand these geometries by learning about the math but also by seeing what they should be given the data from intepreting such poems. I made a related post at Math Stack Exchange: Is this set of 6 transformations fundamental to geometry?

21) This emotional theory describes beauty as arising upon the disappearance of one's inner self whereby disgust becomes impossible. It would be meaningful to study what is beautiful in mathematics and why.

4 geometries & 6 transformations between them <=> The Ten Commandments (4 positive and 6 negative)

Nonwishes: Eightfold way: Snake lemma

The Snake Lemma <=> The eightfold way

Nonwishes: Eightfold way: Octonions

The octonions <=> The eightfold way.

Big Picture: From Indefinite to Unimaginable

{$F_1$} - Division of everything into 0 perspectives

Spinor - Going beyond oneself into oneself

Perturbation - Intervention, intercession, miracle

Map of deepest values

Persons

The application of the pumping lemma (Hopcroft & Ullman, p.57) is expressed as a dialogue with an adversary where the adversary chooses the existential quantifiers and we choose the universal quantifiers. Thus this is an example of a division of perspectives and the use of persons such as You and I.

Standard model - gauge theories - Indefinite / Definite / Imaginable / Unimaginable

Operations -1, +1, +2, +3 correspond to time (-1) and three dimensions of space (+1,+1,+1).

Gravity - r2 law - Yoneda lemma - Universality - Global quantum

Symmetry breaking from unstable symmetry - Higgs particle is the vibration that breaks the symmetry
Gaps and cracks - fixed points - deepest values
Walks on binary trees (labeled by the threesome)
might handle: renormalization, inflation, expansion (dark energy), dark matter, quantum computing
harmonization through prayer
after life through clarity of deepest value
configures like an avalanche or like a lightning bolt
orthogonal bases arise like order out of chaos
Maxwell's demon - Bible story - how physicists talk about the global quantum - that you run out of tape
Experiment connects global questions and local answers, it is highly contrived.

God's going beyond himself: {$F_1$}

The state of contradiction <=> God

The Field with One Element <=> God

The "field with one element" as being interpretable as 0, 1 and infinity.
Moebius transformations.

Contradiction: Godel's Incompleteness Theorem

I would like to learn more what logic is all about, in practice. I have taken the mathematical logics course, am familiar with Goedel's theorems and have done graduate study in recursive function theory.

God's Dance: SU(2)

Goals for Math4Wisdom

Goals for Math 4 Wisdom

Express my concepts in terms of math.
Show that my concepts are relevant and fruitful in math.
Present a language for
Foster a community.
Overview all of math - the areas, concepts, questions, results...
Identify and appreciate the key concepts behind mathematics.
Understand and apply the nature of mathematical beauty.
Address the shortage of materials for appreciating, contemplating, exploring advanced mathematical topics and especially, gaining a sense of the big picture.
- A sort of guide for mountain climbers (or cave explorers or mental prison explorers).
Show the usefulness of wisdom as a guide in making sense of mathematics and the relevance of various mathematical topics to expressing wisdom.
- A bit like an alternative reality for wizards except its real - Jesus, Buddha, Mohammed, Harry Potter.
Show the reality of cognitive frameworks.
Way to engage those who might work together.

General idea of my philosophy

Relate the definite and the indefinite.
Math is most definite. So show how the indefinite relates.
For example, how axiomatic mathematics is inspired by nonaxiomatic premathematics.

General approach

Ways of figuring things out in math.

Theory regarding the Facts

Search for Definition ultimately leads to the Indefinite
The Indefinite, Definite, Imaginable, Unimaginable
Something like God
- Recommend Carroll's video "Why God is not a good theory"
- Omniscient vantage point - important for gaining intuition about knowing everything - including how I relate to God and how others relate to God
- the spirit of everything - everything is the structure of God
- The zeroth person.
- The vantage point of the one who loves us more than we love ourselves.
The state of contradiction - God
Proof by contradiction - how can anything come from God
God goes beyond himself into himself
Goedel's theorems
General question - how can a consistent system arise from inconsistency - that is where Bott's periodicity comes in
Another model: F1 - zero, one, infinity
Fixed points
SU(2) relates zero, one, infinity

Relevance of God - source for mathematical intuition

Peacemaking - "love your enemy" (unconditionality allows for negative numbers)
Check oneself (myself) when one challenges another to grow, am I doing it for selfish reasons?
Be able to live closer to the edge, thus learn more about life, not in an ivory tower - economically, socially.

Not math for its own sake

but stay open minded
Baez 5, 8, 24 - favorite numbers - will talk about them
Projective geometry for octonions, magic square
Albert R+C+H
R+C+H+O and octonions
E8
cellular automata

Summary of wisdom

Eternal life
Overview of theological purpose - God does not have to be good
Longer summary at the end of the series

Goals for wisdom

Goals for wisdom

Main ways the indefinite is important.
Solve technical issues.
Relate different houses of knowledge.

Goals for language

Create a language for working together as a scientific community.
I look to math as a standard of truth for such expression, for such a language.

Goals for community

Support inclusive harmony of self-realization of all people - "meaningful inclusion".
Shared question, "How to love each other more"
Sharing life experiences, deepest values, investigatory questions, etc.
My personal goal is to express myself fully as I wish for others as well.
So I am expressing myself through arts and with examples from all of life.

Personal goals

Find support and income to get by.

Credits

''He gave it to me - started a fire burning in me - he gave it to me -

Nuotraukas draugų, kurie padėjo.

Introduction. Research Program.
ABC's of Thinking-in-Parallel
- 3-Track Mind for Learning. Derived functors.
- 4-Track Mind for Knowledge. Yoneda Lemma.
- 2-Track Mind for Existence.
Divisions, Conceptions, Circumstances
More Sophisticated Thinking-in-Parallel
- 5-Track Mind for Deciding. Dual causality and QFT.
- 6-Track Mind for Morality. Snake Lemma.
- 7-Track Mind for Dualities
24 Keys For Solving Math Problems
Map of Math: Affine, Projective, Conformal, Symplectic Geometry
Bott Periodicity: Unfolding of Thinking-in-Parallel
Poincare Group: Organizing Structures and Perspectives
Big Picture: From Indefinite to Unimaginable