• View
• Edit
• History
• Print

Research Program Fivesome, Meixner polynomials, Charlier polynomials, Laguerre polynomials, Hermite polynomials, MeixnerPollaczek polynomials

Moments

This paper has complete information about the moments of the orthogonal Sheffer polynomials: Jiang Zeng. Weighted Derangements and the Linearization Coefficients of Orthogonal Sheffer Polynomials. Note that in Chihara's book {$(\beta)_n$} is the rising factorial and I think Zeng follows this same convention used in the theory of special functions, whereas in combinatorics it signifies the falling factorial.

Weights (Distributions)

Polynomial	Weight {$w(x)$}	Moments	Moment generating function
Meixner	step function {$\frac{\lambda^t(\beta)_t}{t!}$} on interval {$[t,t+1)$}	ordered Bell numbers {$\frac{1}{(1-c)^n}\sum_{\sigma\in S_n}c^{\textrm{dec}\;\sigma}\beta^{\textrm{cyc}\;\sigma}$}	{$(\frac{1-c}{1-ce^t})^\beta$} or {$\frac{1}{1-\lambda(e^t-1)}$}
Charlier	step function {$e^{-\lambda}\frac{\lambda^t}{t!}$} on interval {$[t,t+1)$}	Bell numbers {$\sum_{\pi\in\mathcal{P}_n}a^{\textrm{bloc}\;\pi}$}	{$e^{\lambda(e^t-1)}$}
Laguerre	{$x^\alpha e^{-x}$} from {$[0,\infty)$}	permutations {$(\alpha + 1)_n$}	{$\frac{1}{(1-t)^{\alpha + 1}}$}
Hermite	{$e^{-x^2}$} from {$(-\infty,\infty)$}	perfect matchings {$(n-1)!!=1\cdot 3 \cdots (2n-1)$}	{$e^{\frac{1}{2}t^2}$}
Meixner-Pollaczek	{$\frac{|\Gamma(\frac{\eta+ix}{2})|^2}{|\Gamma(\frac{\eta}{2})|^2}e^{x\;\textrm{tan}^{-1}\delta} $} or {$e^{(2\phi-\pi) x}|\Gamma(\lambda + ix)^2|$} from {$(-\infty,\infty)$}	alternating permutations {$\delta^n\sum_{\sigma\in S_n}(1+\frac{1}{\delta^2})^{\textrm{max}\;\sigma}\eta^{\textrm{cyc}\;\sigma}$}	{$(\cos t - \delta\sin t)^{-\eta}$}

The leftmost formula for the Meixner-Pollaczek weight function is given by Zeng 1997, and the rightmost formula is from Wikipedia.

For a positive even integer {$n=2N$} we have

{$$\frac{|\Gamma(\frac{n+ix}{2})|^2}{|\Gamma(\frac{n}{2})|^2}e^{-x\textrm{tan}^{-1}\delta} = \frac{\pi}{2}x \;\textrm{csch}(\frac{\pi x}{2}) \prod_{k=1}^{N-1}(1+\frac{x^2}{4k^2})e^{-x\textrm{tan}^{-1}\delta}$$}

and for a positive odd integer {$n=2N+1$} we have

{$$\frac{|\Gamma(\frac{n+ix}{2})|^2}{|\Gamma(\frac{n}{2})|^2}e^{-x\textrm{tan}^{-1}\delta} = \textrm{sech}\;(\frac{\pi x}{2})\prod_{k=1}^{N}(1+\frac{x^2}{(2k-1)^2})e^{-x\textrm{tan}^{-1}\delta}$$}

Note that in the case of the Charlier polynomials there arises in the Poisson distribution a factor {$e^{-\lambda}$} which I think comes from the norm over the whole space. So I have to look for such factors in each case.

Math Stack Exchange. Exponential generating function of the falling factorial.

Levent Kargın. Some formulae for products of Fubini polynomials with applications.

Khan. Some Results on q-Analogue Type of Fubini Numbers and Polynomials

Josef Meixner: His life and his orthogonal polynomials

---

Moments

The {$k$}th moment {$\mu_k$} of an orthogonal polynomial is gotten by integrating {$x^k$} against the weight {$\textrm{dw}$}.

{$$\mu_k=\int x^k \textrm{dw}$$}

In the case of the various Sheffer polynomials, these moments are fundamental numbers in combinatorics which count the most basic objects.

Meixner	ordered Bell number	ordered set partitions of n (weak orderings)
Charlier	Bell number {$B_n$}	set partitions of n (equivalence relations)
Laguerre	n!	permutations of n (strict orderings)
Hermite	(n-1)!! or 0	permutations of n where each cycle is a pair
Meixner-Pollaczek	Secant number {$A_{2n}$}	alternating permutations of 2n

I need to check the secant numbers... A relevant paper is P.Njionou Sadjang, W.Koepf, M.Foupouagnignia. On moments of classical orthogonal polynomials. 2015. I'm also curious about the Jacobi polynomials and other polynomials.

Meixner moments are {$\mu_n(\beta,c)=(1-c)^{-\beta}\sum_{k\geq 0}k^nc^k\frac{(\beta)_k}{k!}$}.

{$\mu_n(\beta,c)=(1-c)^{-n}\sum_{\sigma\in S_n}\beta^{\textrm{cycle}(\sigma )}c^{\textrm{non-excedances}(\sigma)}$}

where the non-excedances of a permutation are the number of elements {$i\in \{1,\dots,n\}$} such that {$i\geq \sigma(i)$}.

The Bell numbers also count permutations that avoid patterns of the form 1-23.

Other non-Sheffer polynomials have interesting moments:

Chebyshev I	{$\binom{2n}{n}$}	ways of choosing half from {$2n$}
Chebyshev II	Catalan {$C_n = \frac{1}{n+1}\binom{2n}{n}$}	{$n$} well formed parentheses

The Hankel determinants of the Catalan numbers are always equal to {$1$}.

Anne de Medicis. The Combinatorics of Meixner Polynomials: Linearization Coefficients

According to Chihara, the moments of the Meixner-Pollaczek polynomials, in the special case {$\eta=0, \zeta=k=1,2,3,\dots$} are given by {$\textrm{sech}^kt=\sum_{m=0}^{\infty}E_m^{(k)}\frac{t^m}{m!}$}, the generating function for the Euler numbers.

Xavier Viennot. Une Theorie Combinatoire des Polynomes Orthogonaux Generaux

Interpreting Permutations as Moments

Zeng has an interpretation of the moment

{$$L(x^n)=\sum_{\sigma\in S_n}u_1^{ad\sigma} u_2^{da\sigma} u_3^{aa\sigma} u_4^{dd\sigma} a_1^{fix\sigma} b_1^{cycle\sigma}$$}

Here {$ad\sigma$} means number of ascents-descents, {$da\sigma$} – descents-ascents, {$aa\sigma$} – ascents-ascents, {$dd\sigma$} descents-descents, {$fix \sigma$} – fixed points, and {$cycles \sigma$} – cycles.

For us we have {$k=u_1u_2$} but also {$k=(-\alpha)(-\beta)$}. And we have {$l=u_3+u_4$} but also {$l=(-\alpha)+(-\beta)$}. Note that the variables in the equation above are simply placeholders. So we can choose to set {$u_1=-\alpha$}, {$u_2=-\beta$}, {$u_3=-\alpha$}, {$u_4=-\beta$}. We also note that descents {$d\sigma=da\sigma + dd\sigma$} and ascents {$a\sigma=aa\sigma + ad\sigma$}. And we can also set {$a_1$}=0, which means that we have no fixed points in our permutations, which means they are all derangements. (Note that cycles include fixed points.) And we have {$c=(b_1-1)k$}, which means {$b_1=\frac{k+c}{k}=\frac{-\gamma}{\alpha\beta}$}. Thus we have:

{$$L(x^n)=\sum_{\sigma\in S_n}(-\alpha)^{a\sigma} (-\beta)^{d\sigma} 0^{fix\sigma}(\frac{-\gamma}{\alpha\beta})^{cycle\sigma}$$}

But I should work with the formula given by Zeng. The paper by Kim and Zeng explains how to interpret this for each of the five orthogonal Sheffer polynomials.

Note that, with my variables, we can write {$-\alpha=u_1=u_4$} and {$-\beta=u_2=u_3$}.

Meixner {$\alpha, \beta$}

Chihara's formula for the Meixner distribution, in my notation: {$\omega(x)=\omega((\alpha -\beta)n) = \left(\frac{\alpha}{\beta}\right)^n\binom{c+n-1}{n}$} at {$x=(\alpha-\beta)n\;\;\;n=0,1,2,\dots$}

Set {$a=u_1=u_4=-\alpha=\frac{v}{1-v}, u_2=u_3=-\beta=\frac{1}{1-v}$}. We can think of the mean as moving with regard to the step {$\frac{\beta}{\alpha}$}. Then

{$\mathcal{L}(x^n)=(\frac{v}{1-v})^n\sum_{\sigma\in\mathcal{S}_n}b^{\textrm{cyc}\;\sigma}v^{-\textrm{exc}\;\sigma}$}

{$\mathcal{L}(x^n)=(-\alpha)^n\sum_{\sigma\in\mathcal{S}_n}b^{\textrm{cyc}\;\sigma}(\frac{\beta}{\alpha})^{\textrm{exc}\;\sigma}$}

Charlier {$\beta=0$}

Set {$-\alpha=a=u_1=u_4=u$}, {$-\beta=u_2=u_3=1$}, {$b=s/u$}

{$\mathcal{L}(x^n)=\sum_{\sigma\in\mathcal{S}_n}(-\alpha)^{\textrm{fix}\;\sigma + \textrm{dec}\;\sigma}b^{\textrm{cyc}\;\sigma}$}

Set {$u=0$} and the sum reduces to the generating function of permutations of which each cycle contains only one decadence or is a singleton. Such a permutation is in bijection with a partition of {$[n]$} by identifying each cycle with the underlying set (block).

{$\mathcal{L}(x^n)=\sum_{\pi\in\Pi_n}s^{\textrm{bloc}\;\pi}$}

where {$\Pi_n$} is the set of partitions of {$[n]$}. {$\textrm{bloc}\;\pi$} is the number of blocks in a partition of {$[n]$}.

Laguerre {$\beta=\alpha$}

Set {$-\alpha=-\beta=1=a=u_1=u_2=u_3=u_4$} Then

{$\mathcal{L}(x^n)=\sum_{\sigma\in\mathcal{S}_n}b^{\textrm{cyc}\;\sigma}$}

Hermite {$\beta=\alpha=0$}

Set {$u_1=u_2=\sqrt{u}$}, {$u_3=u_4=0$}, {$b=u^{-1}$}. Then

{$\mathcal{L}(x^n)=\sum_{\sigma\in\mathcal{D}_n^*}b^{\textrm{cyc}\;\sigma-\textrm{ad}\;\sigma} $}

{$\mathcal{D}_n^*$} is the set of derangements of {$[n]$} without double-descents or double-ascents. Let {$u\rightarrow 0$}, the sum reduces to {$0$} when {$n$} is odd, and is the number of involutions without fixed points when {$n$} is even.

{$$L(x^n)=(-\gamma)^{\frac{n}{2}}\sum_{\sigma\in \textrm{Involutions}}$$}

Meixner-Pollaczek {$\beta = \bar{\alpha}$}

Set {$-\alpha=u_1=u_4=a+i, -\beta=u_2=u_3=-\bar\alpha = a-i$}. We have

{$\mathcal{L}(x^n)=\sum_{\sigma\in\mathcal{S}_n}(a + i)^{\textrm{dec}\;\sigma}(a - i)^{\textrm{exc}\;\sigma}a^{\textrm{fix}\;\sigma}c^{\textrm{cyc}\;\sigma}$}

Kim and Zeng show combinatorially that this complex expression equals the real expression

{$\mathcal{L}(x^n)=\sum_{\sigma\in\mathcal{S}_n}a^{n-2\;\textrm{ad}\;\sigma}(a^2+1)^{\textrm{ad}\;\sigma}c^{\textrm{cyc}\;\sigma}$}

where {$\textrm{ad}$} stands for ascents-descents, which is to say, peaks {$\sigma^{-1}(i)<i>\sigma(i)$}. This formula shows that these moments are real. Whereas I think that globally the mean moves by an angle in the complex plane.

Narrative of moments

Consider how the narrative of particle scattering manifests itself in the moments.

Suppose that {$\alpha$} and {$\beta$} are real numbers.

---

Distributions

Meixner

{$\omega(x)=\left(\frac{\alpha}{\beta}\right)^n\binom{c}{n}$} at {$x=(\alpha-\beta)n\;\;\;n=0,1,2,\dots$}

Charlier

{$\omega(x)=e^{-\frac{\alpha}{\beta}}\left(\frac{\alpha}{\beta}\right)^n\frac{1}{n!}$} at {$x=(\alpha-\beta)n\;\;\;n=0,1,2,\dots$} This doesnt make sense because {$\beta=0$}

Laguerre

Hermite

Meixner-Pollaczek

Calculating distributions from moments

Consider the Fourier transform on finite groups and calculating the inverse Fourier transform.

Meixner

{$\mu_n(\beta,c)=(1-c)^{-\beta}\sum_{k\geq 0}k^nc^k\frac{(\beta)_k}{k!}$}

{$M_x(t)=\mathbb{E}[e^{tX}]=\sum_{n=0}^{\infty}\frac{1}{(1-c)^{\beta}}\sum_{k\geq 0}k^nc^k\frac{(\beta)_k}{k!}\frac{t^n}{n!}$}

{$=\frac{1}{(1-c)^{\beta}}\sum_{k\geq 0}\sum_{n=0}^{\infty}k^nc^k\frac{(\beta)_k}{k!}\frac{t^n}{n!}$}

{$=\frac{1}{(1-c)^{\beta}}\sum_{k\geq 0}\frac{c^k}{k!}(\beta)_k\sum_{n=0}^{\infty}\frac{(kt)^n}{n!}$}

{$=\frac{1}{(1-c)^{\beta}}\sum_{k\geq 0}\frac{c^k}{k!}(\beta)_k e^{kt}$}

Charlier

Math Stack Exchange. Given Bell numbers as moments, derive the Poisson distribution.

Laguerre

Math Stack Exchange. How to integrate...

Hermite

Meixner-Pollaczek

{$\textrm{sech}^kt=\sum_{m=0}^{\infty}E_m^{(k)}\frac{t^m}{m!}$} gives the moments {$E_m^{(k)}$} where {$k$} is a variable.

{$\hat{w}(\xi)=\sum_{n=0}^{\infty}\frac{(-2\pi i)^n}{n!}E_n^{(k)}\xi^n = \sum_{n=0}^{\infty}E_n^{(k)}\frac{(-2\pi i\xi)^n}{n!} = \textrm{sech}^k(-2\pi i\xi)$}

{$=(\frac{2}{e^{-2\pi i\xi}+e{2\pi i\xi}})^k=(\frac{2}{2\cos (2\pi\xi)})^k=\textrm{sec}^k(2\pi\xi)$}

{$w(x)=\int_{\infty}^{\infty}\textrm{sec}^k(2\pi\xi)e^{i2\pi\xi x}d\xi$}

Given the moments, I want to calculate a distribution. I am trying to understand how the distribution expresses the combinatorics inherent in the moments.

The moment generating function {$M_X(t)$} encodes the moments. It is related to the two-sided Laplace transform of its probability density function {$f_X(x)$} in this way: {$M_X(t)=\mathcal{L}\{f_X\}(-t)$}. This follows from the definition {$\mathcal{L}\{f_X\}(s)=\int_{-\infty}^{\infty}e^{-sx}f_X(x)dx$} and the expression {$M_X(t)=E[e^{tX}]=\int_{-\infty}^{\infty}e^{tx}f_X(x)dx$}.

I can use the inverse Laplace transform to get:

{$f(t)=\mathcal{L}^{-1}\{F(s)\}(t)=\frac{1}{2\pi i}\lim_{T\rightarrow\infty}\int_{\gamma -iT}^{\gamma +iT}e^{st}F(s)ds$}

where the integration is done along the vertical line {$\textrm{Re}(s)=\gamma$} in the complex plane such that {$\gamma$} is greater than the real part of all singularities of {$F(s)$} and {$F(s)$} is bounded on the line. If all singularities are in the left half-plane or if {$F(s)$} is an entire function, then we can set {$\gamma = 0$} and the formula becomes the inverse Fourier transform.

For discrete distribution we need the Z-transform.

Math Stack Exchange. Bell numbers and moments of the Poisson distribution

{$x^n=\sum_{k=0}^n(x)_k \begin{Bmatrix}n\\k\end{Bmatrix} = \sum_{k=0}^n x(x-1)\cdots (x-n+1) \begin{Bmatrix}n\\k\end{Bmatrix}$}

Note that the distribution for the Meixner polynomials includes a falling factorial which should relate to the Touchard polynomials. Bell numbers count set partitions and Touchard polynomials break them up by the number of parts in the partition. Note also that the Touchard polynomials have a contour integral representation:

{$T_n(x)=\frac{n!}{2\pi i}\oint \frac{e^{x(e^t-1)}}{t^{n+1}}dt$}

Stirling numbers of the second kind {$\begin{Bmatrix} n \\ k \end{Bmatrix}$} count set partitions of an n-element set into k parts. The ordered Bell numbers {$a_n$} can be counted in terms of them.

{$a_n=\sum_{k=0}^{n}k!\begin{Bmatrix} n \\ k \end{Bmatrix}$}

We have

Math Stack Exchange. Generating function with stirling numbers of the second kind. Note the poles.

For ordered Bell numbers, the generating function {$f(z)=\frac{1}{2-e^z}$} has only simple poles, namely at the points {$\log 2 ± 2kπi$} for all integer {$k$}.

---

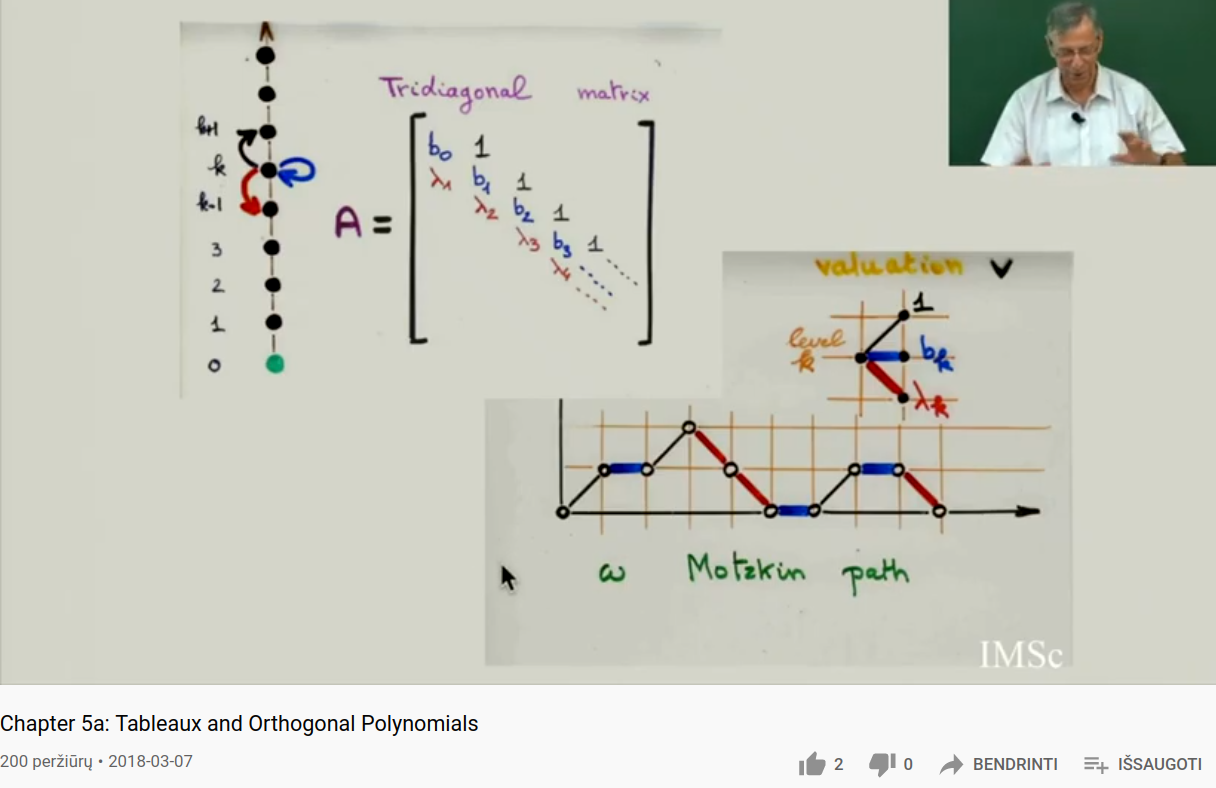
Motzkin paths

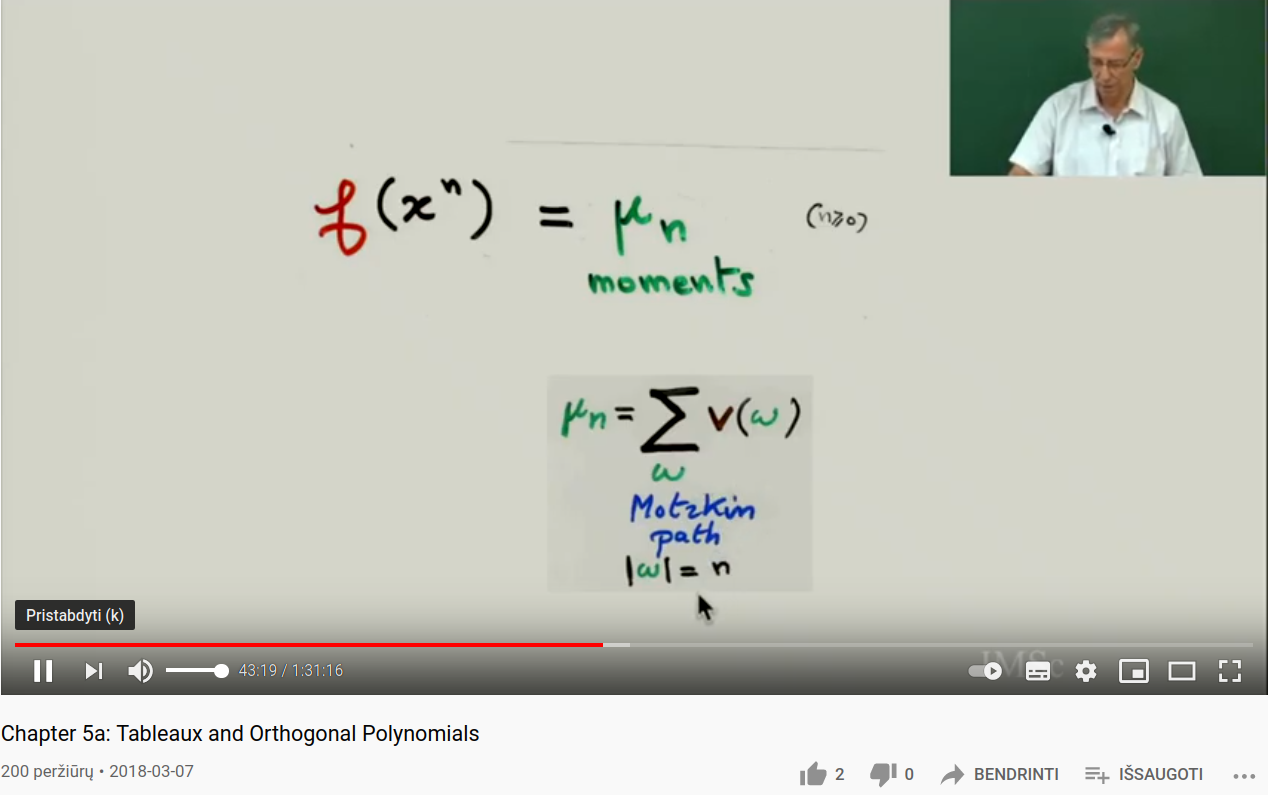
Consider the recurrence relation {$P_{n+1}(x)=(x-b_n)P_n(x)-\lambda_nP_{n-1}(x)$}.

The moments {$\mu_n$} are given by the sum of the weights {$1$}, {$b_k$}, {$\lambda_k$} on the Motzkin path length {$n$}. Here {$k$} is the altitude of the path at a particular point. Each step along the path is given by the application of the tridiagonal matrix. The Motzkin path of length {$n$} arises from multiplying the matrix {$n$} times and considering those paths that "do nothing" in that they start and end at {$k=0$}.

Note that for Sheffer polynomials we furthermore have that {$b_k=ak+b$} and {$\lambda_k=k(ck+d)$} where {$c\geq 0$}, {$c+d>0$}.

Then the classification is:

• Hermite {$a=0$}, {$c=0$} thus {$b_k$} constant, {$\lambda_k$} constant
• Charlier {$a\neq 0$}, {$c=0$} thus {$b_k$} linear in {$k$}, {$\lambda_k$} constant
• Laguerre {$a\neq 0$}, {$a^2-4c=0$} thus {$(b_k^2~4\lambda_k$}
• Meixner {$a\neq 0$}, {$a^2-4c>0$}
• Meixner-Pollaczek {$a\neq 0$}, {$a^2-4c<0$}

Imagine the graph as representing motion in time (horizontally) up and down the vertical axis. The weight {$b_k$} signifies staying in place and the weight {$\lambda_k$} signifies taking a step down (alternatively, a step up). Then as we move away, we need to worry about returning. Squaring the movement away from the origin gives added weight to this deviation, as in the method of least squares.

---

---

---

The Hankel Determinant

I think the Hankel determinant indicates whether the moments are valid in that they are linearly independent.

From Chihara's book:

---

---

---

Automata

The moments of the Hermite polynomials can be understood to encode Dyck paths, which is to say, valid sequences of left and right parentheses. Thus they may be understood as the valid strings for a pushdown automata accepting a context free grammar. Interpret the moments of other polynomials in this way! And how do the involutions relate to the Catalan numbers? Note also how the Motzkin paths for involutions do not have lateral movements, which is where everything interesting happens, the inside of the moment's analogue to the tree or clock.

Unrelated

Jacobi polynomials have weight: {$(1-x)^{\alpha}(1+x)^\beta$}