- Recently changed pages
- News Archive
- Math4Wisdom at Jitsi
- News at BlueSky
- News at Mathstodon
- Research Notes
Study Groups
Featured Investigations
Featured Projects
Contact
- Andrius Kulikauskas
- m a t h 4 w i s d o m @
- g m a i l . c o m
- +370 607 27 665
- Eičiūnų km, Alytaus raj, Lithuania
Thank you, Participants!
Thank you, Veterans!
- Jon and Yoshimi Brett
- Dave Gray
- Francis Atta Howard
- Jinan KB
- Christer Nylander
- Kirby Urner
Thank you, Commoners!
- Free software
- Open access content
- Expert social networks
- Patreon supporters
- Jere Northrop
- Daniel Friedman
- John Harland
- Bill Pahl
- Anonymous supporters!
- Support through Patreon!
Combinatorial alternative to wave function, Research program fivesome, Kim Zeng trees, Moments
These are my notes for the
Kim Zeng involution
The Linearization formula
{$\mathcal{L}(P_n(x)^2)=n!(c)_n(\alpha\beta)^n$} where {$(c)_n$} is the rising factorial
Combinatorially, Kim and Zeng's formula for linearization coefficients yields
{$\mathcal{L}(P_n(x)^2)=(\alpha\beta)^n\sum_{\sigma\in\mathcal{D}_{(n,n)}}c^{\textrm{cyc}\;\sigma} $}
{$\sum_{\sigma\in\mathcal{D}_{(n,n)}}c^{\textrm{cyc}\;\sigma}=n!(c)_n$}
For example, if we define our generalized derangements on the odds {$\{1,3,5,7,\dots\}$} and the evens {$\{a,b,c,d,\dots\}$}, and consider all permutations of the evens, we have:
| {$c$} | {$(1 a)$} |
| {$2c(c+1) = 2(c^2 + c)$} | {$(1 a)(3 b),(1 a 3 b)$} |
| {$6c(c+1)(c+2) = 6(c^3 + 3c^2 + 2c)$} | {$(1 a)(3 b)(5 c), (1 a 3 b)(5 c), (1 a 5 b)(3 c), (1 a)(3 b 5 c), (1 a 3 b 5 c), (1 a 5 b 3 c)$} |
| {$24c(c+1)(c+2)(c+3) = 24(c^4 + 6c^3 + 11c^2 + 6c)$} | {$(1 a)(3 b)(5 c)(7 d),$} |
| {$(1 a 3 b)(5 c)(7 d), (1 a 5 b)(3 c)(7 d), (1 a 7 b)(3 c)(5 d), (1 a)(3 b 5 c)(7 d), (1 a)(3b 7c)(5 d), (1 a)(3 b)(5 c 7 d), $} | |
| {$(1 a 3 b 5 c)(7 d), (1 a 5 b 3 c)(7 d), (1 a 3 b 7 c)(5 d), (1 a 7 b 3 c)(5 d), (1 a 5 b c 7)(d 3),(1 a 7 b 5 c)(3 d), (1 a)(3 b 5 c 7 d), (1 a)(3 b 7 c 5 d)$} | |
| {$(1 a 3 b)(5 c 7 d), (1 a 5 b)(3 c 7 d), (1 a 7 b)(3 c 5 d), $} | |
| {$(1 a 3 b 5 c 7 d), (1 a 3 b 7 c 5 d), (1 a 5 b 3 c 7 d), (1 a 5 b 7 c 3 d), (1 a 7 b 3 c 5 d), (1 a 7 b 5 c 3 d)$} |
If {$c=1$}, then we get {$n!n!$} terms. In other words, {$(1)_n=n!$}
Moments
The formula can be interpreted by calculating the moments {$\mathcal{L}(x^n)$}.
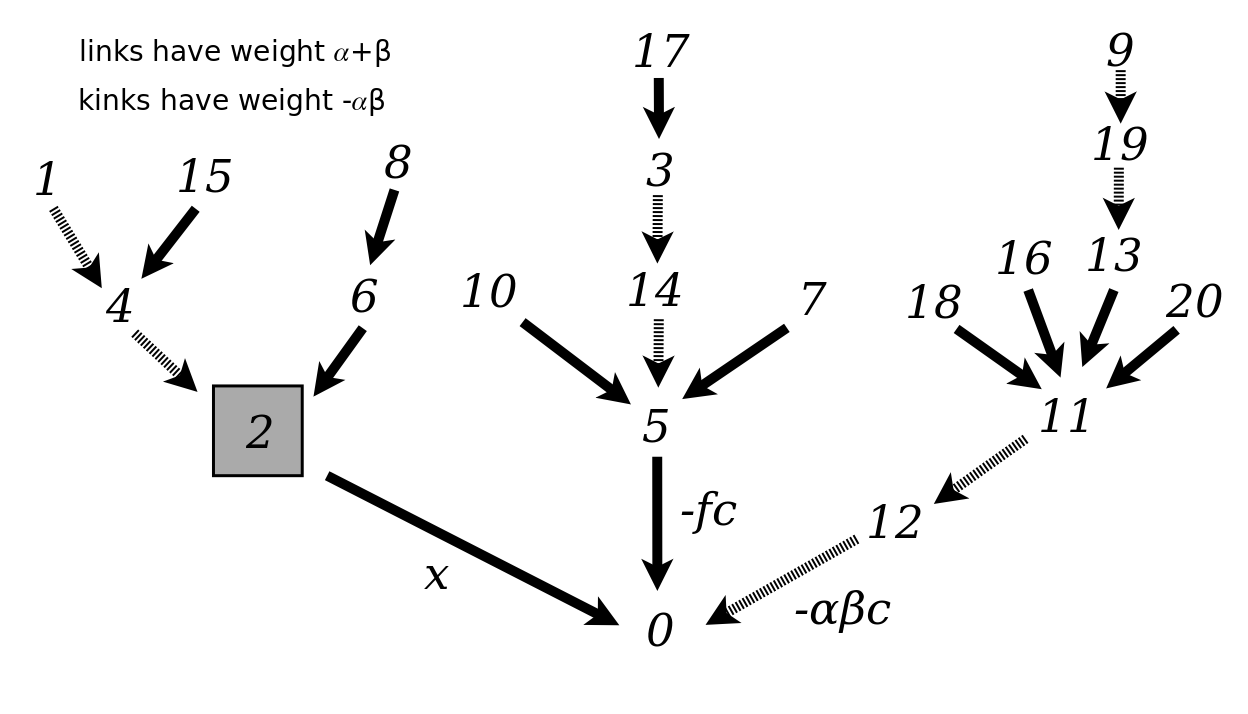
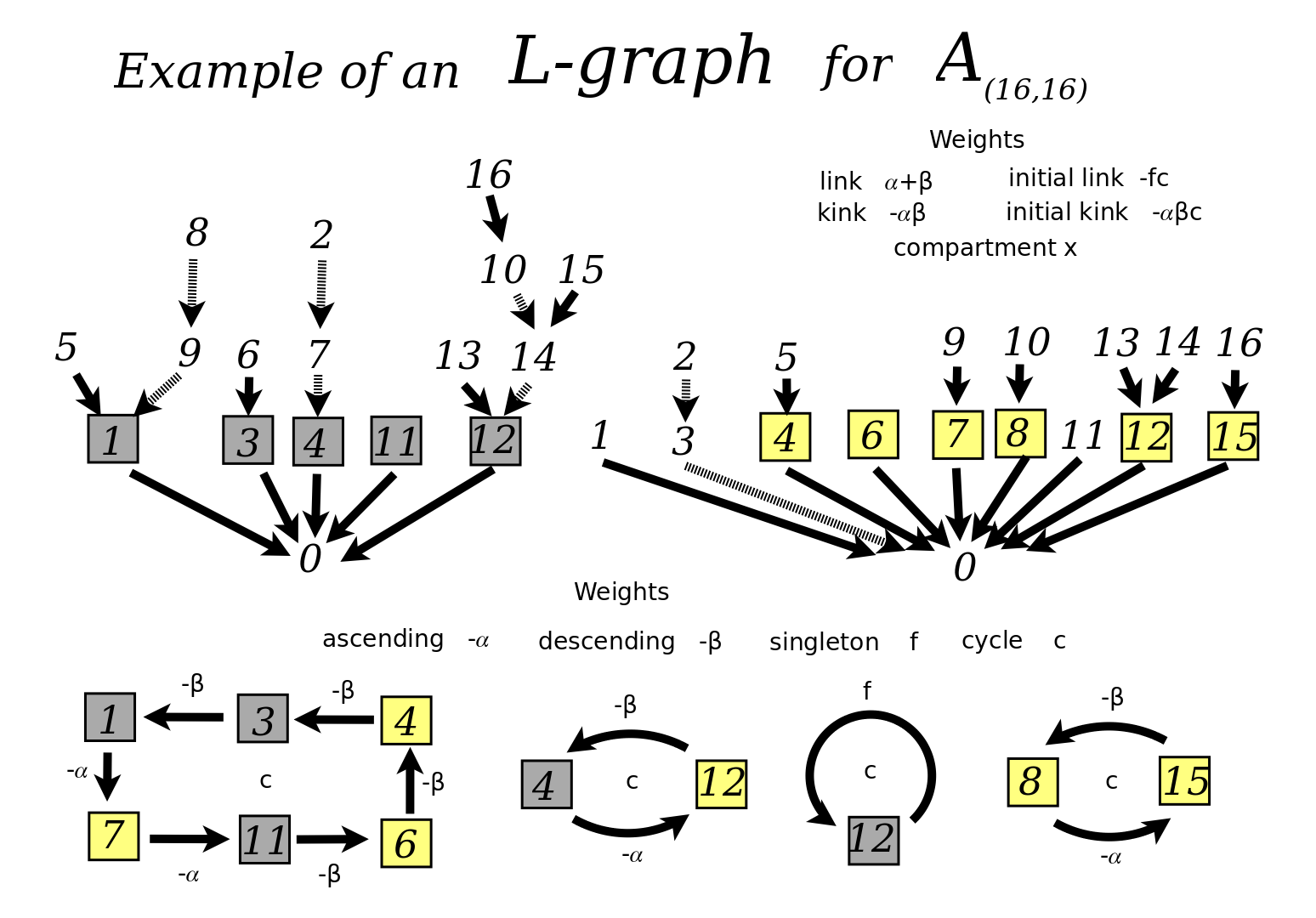
{$\mathcal{L}(x^n)=\sum_{\sigma\in S_n} (-\alpha)^{\textrm{asc}\;\sigma} (-\beta)^{\textrm{desc}\;\sigma} f^{\textrm{fix}\;\sigma} c^{\textrm{cyc}\;\sigma} $}
For {$A_{(n,n)}$}, skew derangements and generalized derangements are the same
Any generalized derangement without color matches is a skew derangement. Note that in the case of {$A_{(n,n)}$} there are no double ascents (and no double descents) and so there are no color matches.
A skew derangement is a permutation {$\pi$} of {$A_{(n,n}$} that has no color matches, and for which if {$c(a)=c(\pi(a))$}, then {$c(\pi^{-1}(a))\neq c(a)$}, {$c(\pi(a))\neq c(\pi^2(a))$} and the smaller of {$\{a,\pi(a)\}$} is a valley and the larger is a peak. But this case supposes that there are three colors:
{$c(\pi^{-1}(a)) > c(a)=c(\pi(a)) > c(\pi^2(a))$} and {$a <\pi(a)$}
or
{$c(\pi^{-1}(a)) < c(a)=c(\pi(a)) < c(\pi^2(a))$} and {$a > \pi(a)$}
Consequently, since we have two colors, then we simply have that {$c(a)\neq c(\pi(a))$} for all {$a\in (n,n)$}, which means that the skew derangements of {$A_{(n,n)}$} are the generalized derangements of {$A_{(n,n)}$}.
Causal trees
L-graphs