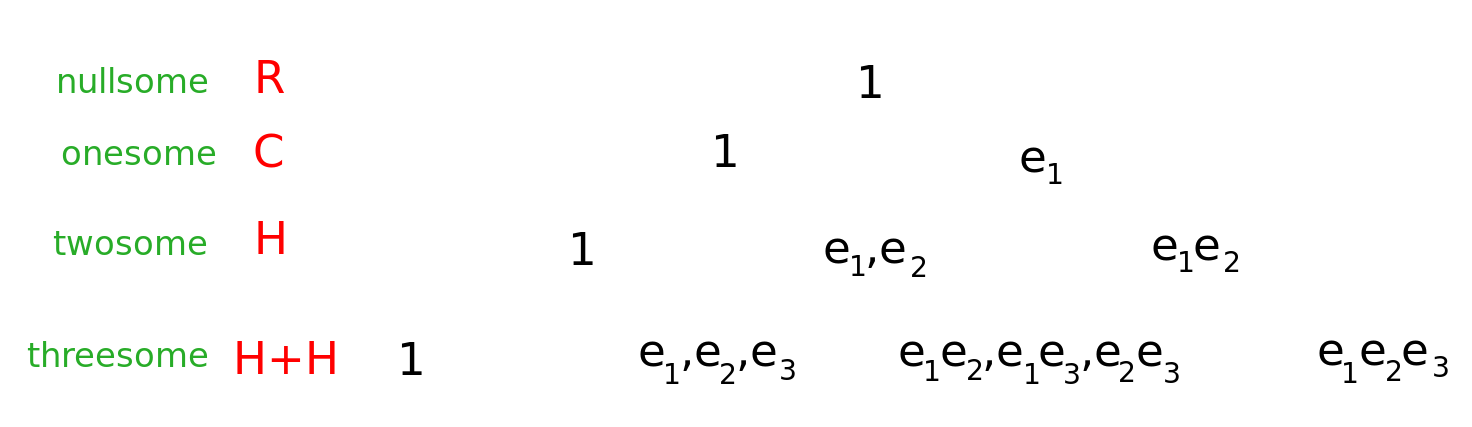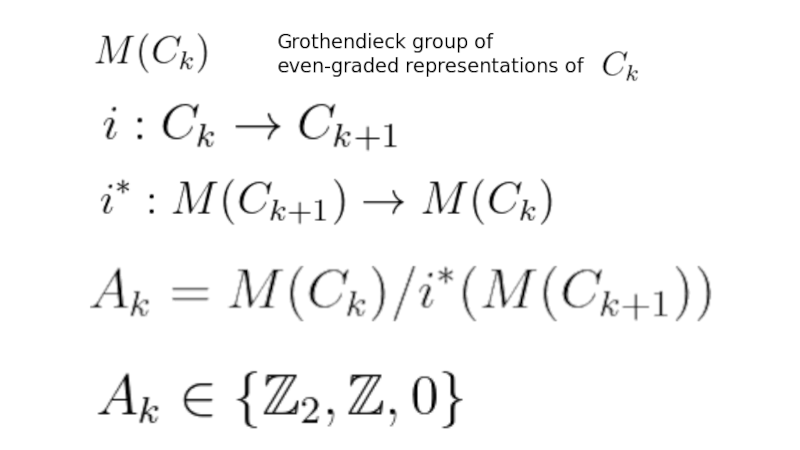Math 4 Wisdom. "Mathematics for Wisdom" by Andrius Kulikauskas.

Bott Periodicity Models Consciousness? Preliminary Exploration

Does Bott periodicity have metaphysical significance? The divisions of everything, the cognitive frameworks which define mental states in Wondrous Wisdom, likewise form an eight cycle.

I, Andrius Kulikauskas, present to John Harland my understanding of Bott periodicity, how to calculate the eightfold pattern using Clifford algebras, and what clues suggest that indeed this may express my model of the mental states on which the Unconscious, Conscious and Consciousness operate.

October 20, 2023.

Presentation about Divisions of everything

I hope this video helps you understand this challenging phenomenon and encourages you to reach out to us so that we can study together! Thank you for leaving comments!

Transcript (edited and improved for clarity, brevity and correctness)

I am Andrius Kulikauskas. This is Math 4 Wisdom, a meeting of our study group on the mathematics of the divisions of everything which are the fundamentals of wondrous wisdom. I am with John Harland of Palomar College. Hello, John.

John: Hello.

Today I will explain to John my best effort to understand Bott periodicity. I've gotten close enough to where I can maybe say something of what I'm trying to do and really, this is about asking for your help! Maybe you know something about Bott periodicity more than I do, and that's quite possible, but maybe this is a milestone in where our research is going. Maybe it'll be interesting. Maybe it'll shine some light for you.

{$\pi_{n}(O(\infty))\simeq\pi_{n+8}(O(\infty))$}

The first 8 homotopy groups are as follows:

{$\begin{align} \pi_{0}(O(\infty))&\simeq Z_2 \\ \pi_{1}(O(\infty))&\simeq Z_2 \\ \pi_{2}(O(\infty))&\simeq 0 \\ \pi_{3}(O(\infty))&\simeq Z \\ \pi_{4}(O(\infty))&\simeq 0 \\ \pi_{5}(O(\infty))&\simeq 0 \\ \pi_{6}(O(\infty))&\simeq 0 \\ \pi_{7}(O(\infty))&\simeq Z \end{align}$}

0:50 Bott periodicity was discovered by Raoul Bott and published in 1957-1959.

Bott periodicity was discovered in 1959 or published in 1959 by Bott. He used Morse Theory. It's an eight-fold periodicity that he described in homotopy theory.

I'll go through these notes. These are for me to talk and so they may be rather scattered.

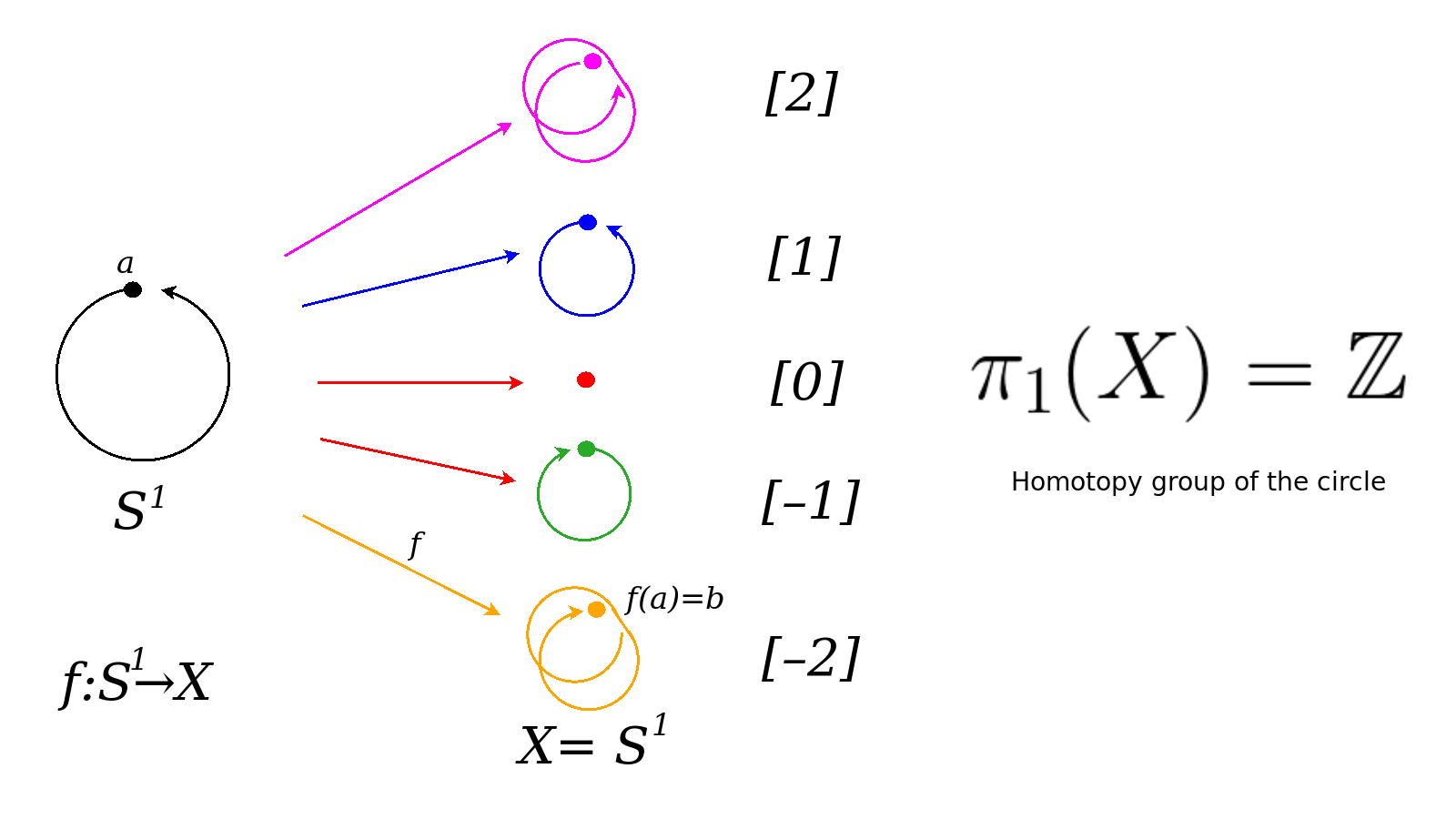
1:20 Homotopy theory is a tool kit in algebraic topology. Homotopy group of a circle.

Bott periodicity in homotopy theory, which is in algebraic topology. You have this whole tool kit of investigating a topological space {$X$} by looking at maps from various types of spheres, which could be simply a loop, for example. A map from a circle {$S_1$} into the space {$X$} yields a loop. That would be a one-dimensional loop but you could look at a two-dimensional sphere, you could look at a three-dimensional sphere, four-dimensional sphere and so on. And when you study these loops you get what are called homotopy groups. Basically, the way it works is you need to choose a point. So you'll choose a point in your space X called a base point and you'll choose a point in the, let's say, circle. You're mapping from the circle, the base point {$a$} and then {$F(a)$} will be a point {$b$} in the space that you're studying. When you do this, you'll map a loop. You'll have lots and lots of loops but basically they'll come into equivalence classes. So, for example, if you're looking at maps from a loop to the circle itself, well, the loops may go on and on and on in that loop. But basically, when you stretch them, when you modify them, they'll give you winding numbers. So maybe it'll just all shrink to a point but maybe it'll wrap around once or twice or three times and so those would all be given different classes. Or you could go in the opposite direction. Those would be, let's say, the negatives. This gives you the group, which would be {$\mathbb{Z}$}, the integers.

3:10 Definition of stable orthogonal group.

John: Can I interrupt you just a moment. {$O(\infty)$}. You're saying, the inductive limit of orthogonal groups. Can you unpack that a little bit.

Yes. So we've been studying Lie groups and the key one that relates to the real numbers is the orthogonal group, which tells you, let's say, for a sphere, it would tell you the rotations but also the reflections, so that you can reflect across. Basically, the things you can do to a sphere that would map the sphere into itself. And so then for the special orthogonal group you would not do the reflections. You can define the orthogonal group in two dimensions {$O(2)$}, three dimensions {$O(3)$}, four dimensions {$O(4)$} for the analogous real sphere. Now these things sit inside each other. Like rotating a circle is sitting inside rotating a sphere, which is sitting inside rotating a four-dimensional sphere. You know, basically what would be a three-dimensional sphere in four dimensions and so on and so on and so on. You could take that whole limit of all these structures and unify them that way. And there may be advantages to that because you could think of them all in one fell swoop. So that would be called {$O(\infty)$}.

4:35 Homotopy groups of O(∞).

So now you can ask yourself, I have this humongous {$O(\infty)$}, all these rotations and all these possible dimensions. What would their homotopic groups be? So {$\pi_0$} would be the number of pieces of it. {$\pi_1$} would be what you get in terms of the classes of loops.

John: You're saying there's two pieces because there's reflections and rotations?

There's two. That's my guess, that's your guess. I think that must be, that's probably what they're saying, but you know I'm talking way above my head. Okay, I think that those are the two, including the reflection or not. And then if you reflect twice you're back to where you started so the reflection goes away. For {$\pi_1$} there's something similar... in terms of the loops somehow there will be two kinds of loops. And this may be related, I'm just guessing, but to like the whole notion of spinors right where you could be going once around or you could be going twice around. If you go run once around then you get a change of state, from state {$+1$} to state {$-1$}. Whereas if you go twice around you will go from {$+1$} back to {$+1$}. So going once around and going twice around let's say would be different but going three times around would be the same as going around once. You know, it's an odd or even type of thing. I'm not sure but that's kind of like the guess. But somehow when you get to talking not about loops mapping into this wonderful creature but when you talk about spheres, two dimensional spheres, three dimensional, and you map those in, then everything collapses to a point. When you throw it up to another dimension you'll get {$\mathbb{Z}$}. So {$\mathbb{Z}$} is something like that winding number right where it's wrapping around, wrapping around, wrapping around, wrapping around somehow in one direction and in the other direction. So you get this very remarkable pattern {$\mathbb{Z}_2, \mathbb{Z}_2, 0, \mathbb{Z}, 0, 0, 0, \mathbb{Z}$}. Someday maybe it'll be a children's song, or the days of the week. What Bott showed was that it repeats, and this was a hugely unexpected thing and very miraculous and stunning.

7:30 Homotopy groups of spheres. 8-fold Bott Periodicity appears there.

And it connects to a lot of things in math very difficult problems. One of the huge difficult problems of the time, and I think this was just as homotopy theory was being invented, like in the 1930s and 40s. This is 1959. They were trying to look at the homotopy groups of spheres which would be basically saying, how do you continuously map {$m$}-dimensional spheres into {$n$}-dimensional spheres? (What is the homotopy group {$\pi_m(S^n)$}?) What does that all look like? How do these spheres wrap around each other? That turns out to this day to be an intractable problem. It's very very difficult and it's especially difficult if {$m \geq 2n-1$}, it's just completely chaotic. (See: Table of homotopy groups) But if you look where {$m < 2n-1$}, it turns out then there is this {$J$}-homomorphism which deals with the case of the special orthogonal group. That's half of these rotations, I presume, and then the ones that don't reflect. It turns out that in those conditions {$\pi_m(S_n)$} is periodic in {$(m-n)\mod 8$}. There's an eightfold pattern and so that'll give you either a cyclic group or a trivial group or instead of this {$\mathbb{Z}$} it will give you a cyclic group with order related to the Bernoulli numbers {$B_{2m}$} which are related to ways of writing out alternating permutations. Bernoulli invented them to calculate sums of powers and so they end up being related to the Riemann zeta function. So something very basic like that is just popping in there, which will yield these very large numbers, in particular cases {$3, 7\mod 8$}. That's just an introduction just to say, this was a big deal in math.

John: It solved the homotopy kind of embedding problem in certain cases you're saying.

Andrius: We can look at the Wikipedia page, Homotopy groups of spheres. I don't understand this but here's this chart. I'm not exactly sure where this is coming in. I think it may come into when one of the dimensions is large. You can see it's a very complicated messy thing. You see the pattern {$\infty, 2, 224, 2, 240$}. See these would be related to the Bernoulli numbers. You get this noise when you get here, this utter chaos. But if you are big enough you get order. So this is some context.

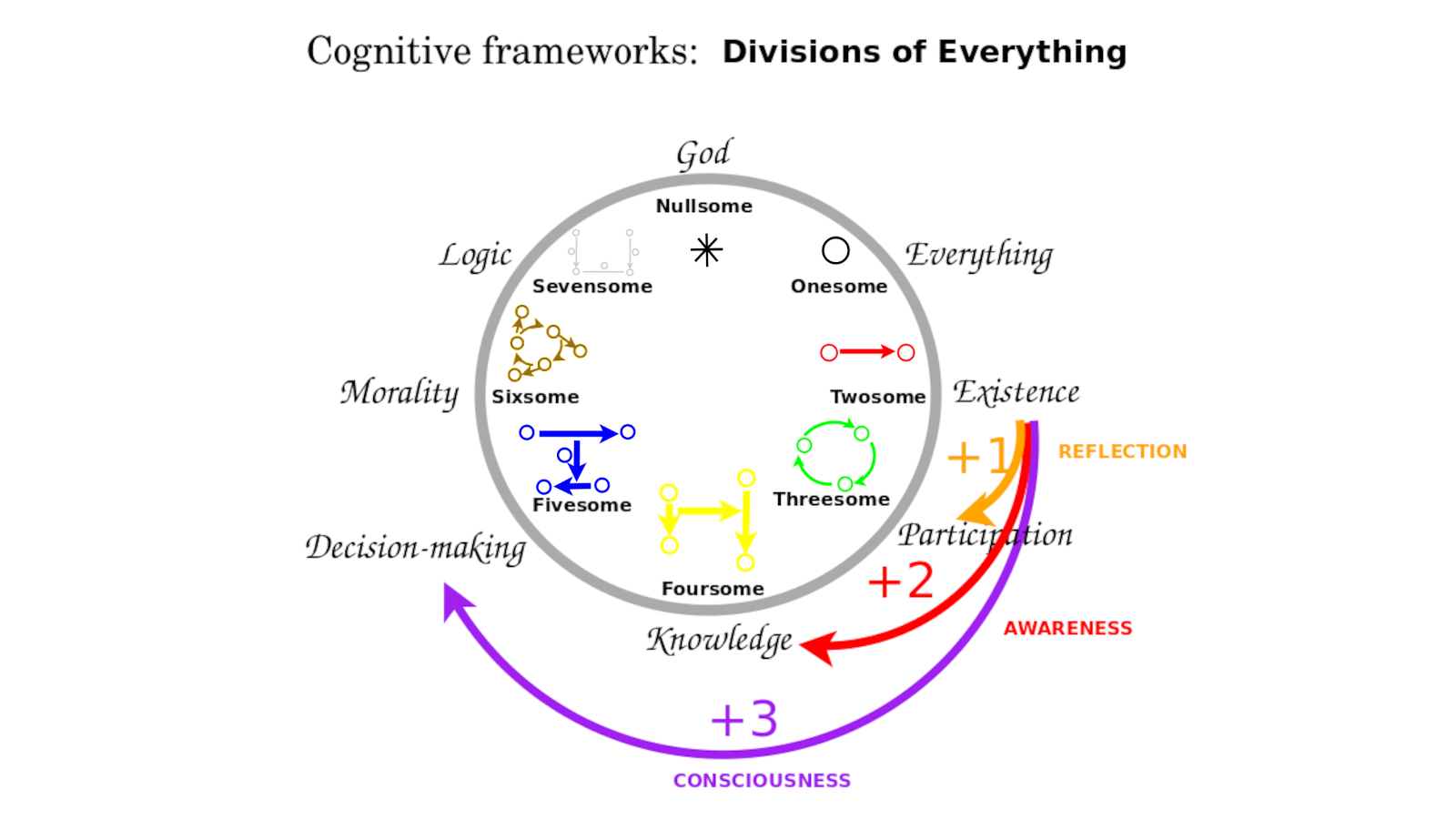
10:55 In 1989, I discovered an eight-cycle of cognitive frameworks. In 2016, I learned of Bott Periodicity.

Why did I become interested? This was 2016. Since childhood, but certainly since 1982, I've been developing this language of Wondrous Wisdom. This resulted in a language of cognitive frameworks I call divisions of everything. When I was 24 years old, was back in 1989, I realized that they form an 8-cycle and that these are basically mental states. If you reflect directly, then you would add one perspective. If you reflected on the reflection that'd be like the Conscious mind, you get two perspectives. You try to balance those, you get three perspectives, Consciousness. So you end up with these shifts that form this periodic system. How would that relate possibly to Bott periodicity? When I found about this eight-fold thing, what is the evidence that this could be more than a coincidence?

12:15 Divisions of everything. Their eightfold periodicity.

This page starts with the division of everything into five perspectives.

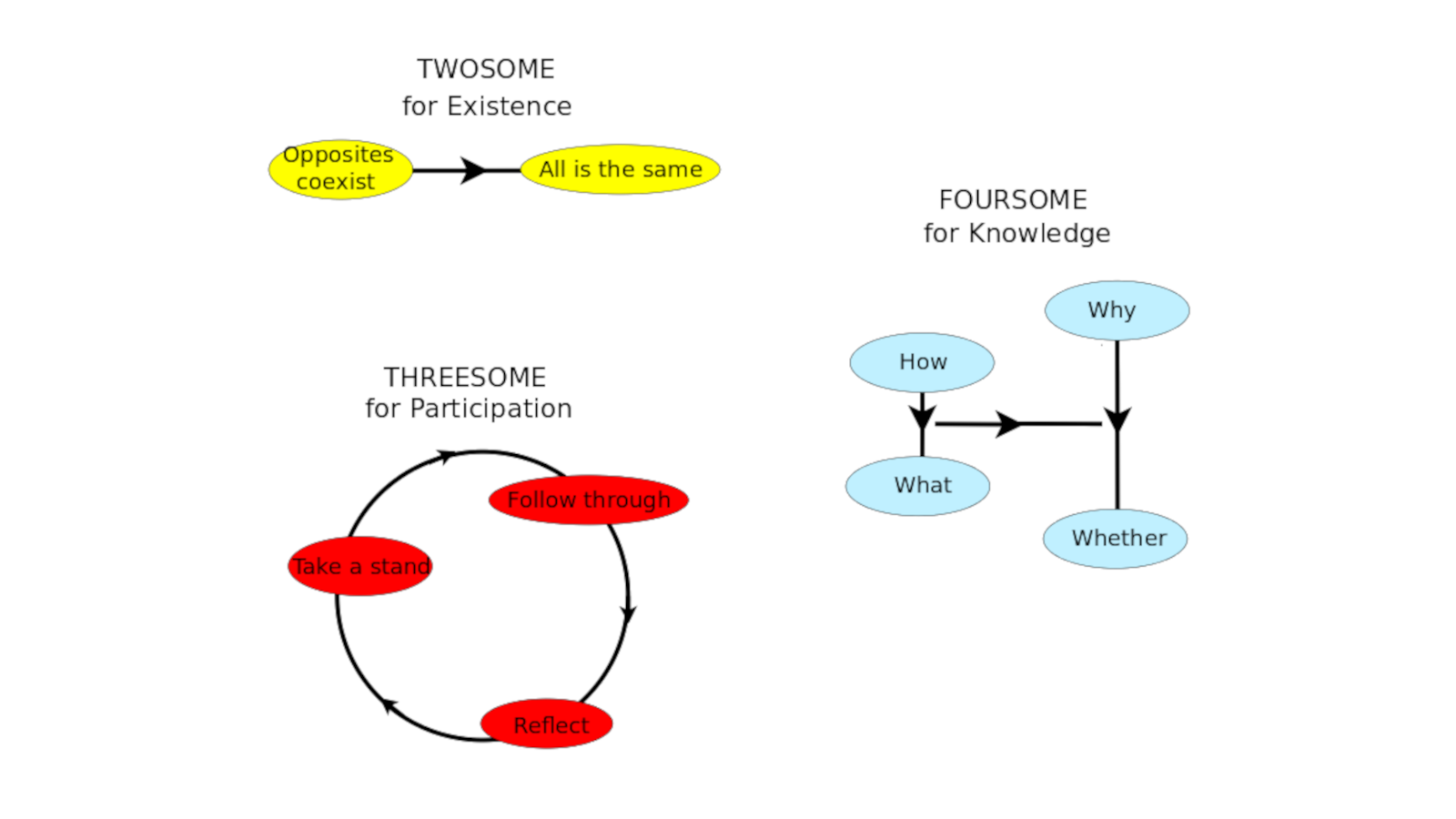
Then these are the very fundamental ones: The twosome says that opposites coexist or all is the same. This is kind of like the complex numbers. The threesome says there's a learning cycle of taking a stand, following through, reflecting, which is a little bit like the three-cycle in the quaternions. This is the foursome for knowledge, saying there are four levels: Whether, What, How, Why, which is another way of looking at the quaternions, as two sets of complex numbers.

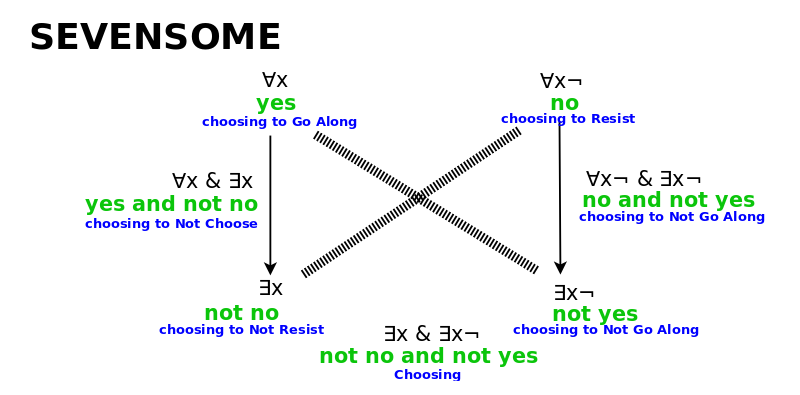
You have a fivesome and a sixsome. Then the crucial thing is that when you get a sevenfold framework for logic, that's when you get a self-standing system. So what I'm describing with these divisions of everything that I've been documenting is how you might start from a state of contradiction and add premises until you get a very fragile but fascinating self-consistent logical system where you can distinguish between Yes and No and things like that, almost like constructing a division.

But if you add an eighth perspective in this logical square - all are good and all are bad - then it just collapses because if everything is good and everything is bad then that distinction means nothing or simply the system is empty. If the system is empty, then you have nothing so it all collapses. So that's in my Wondrous Wisdom, documenting that. That's the reason we have this eight-fold periodicity. So here's another eight-fold periodicity - Bott periodicity. Is there any chance they could be the same on some level?

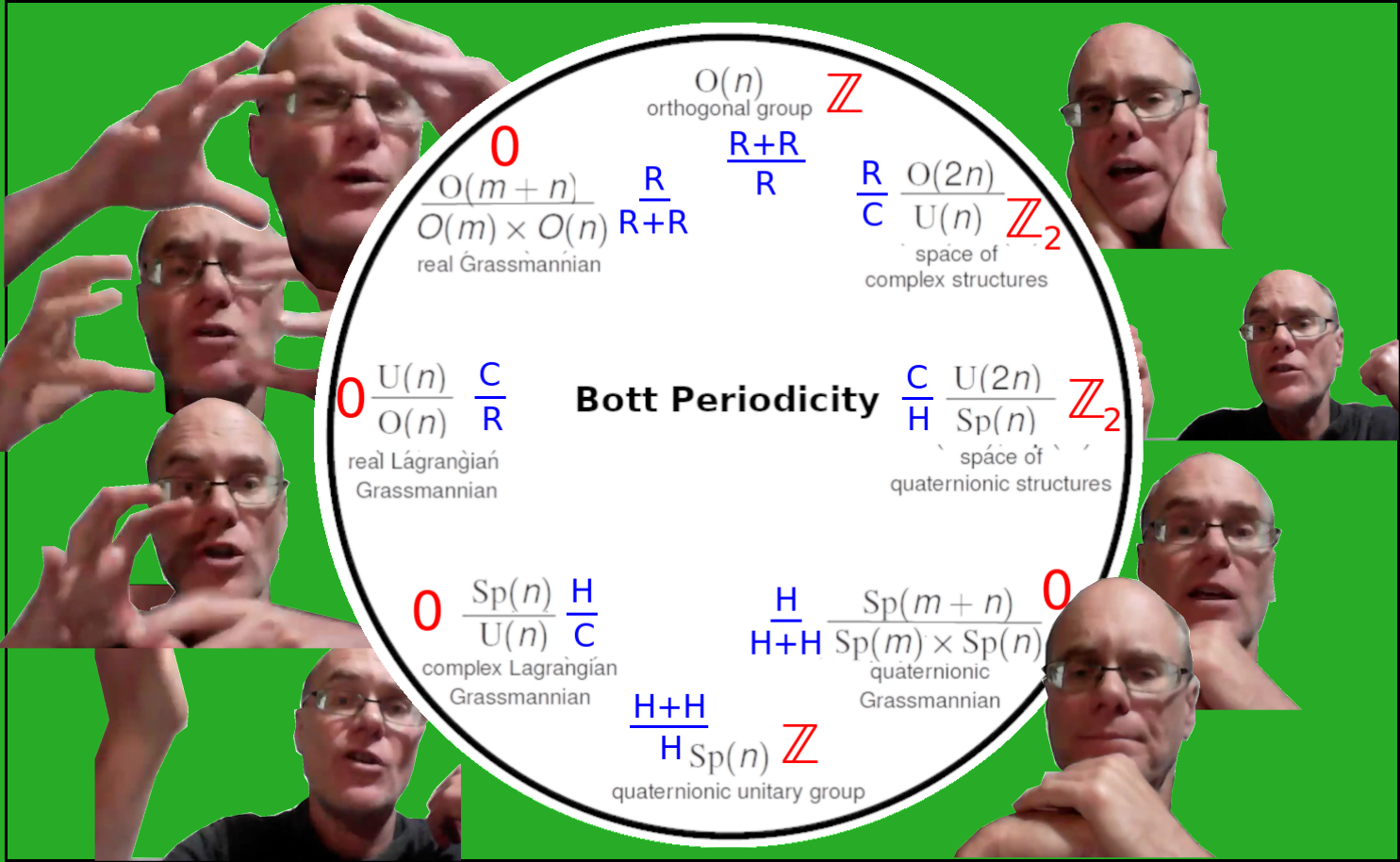
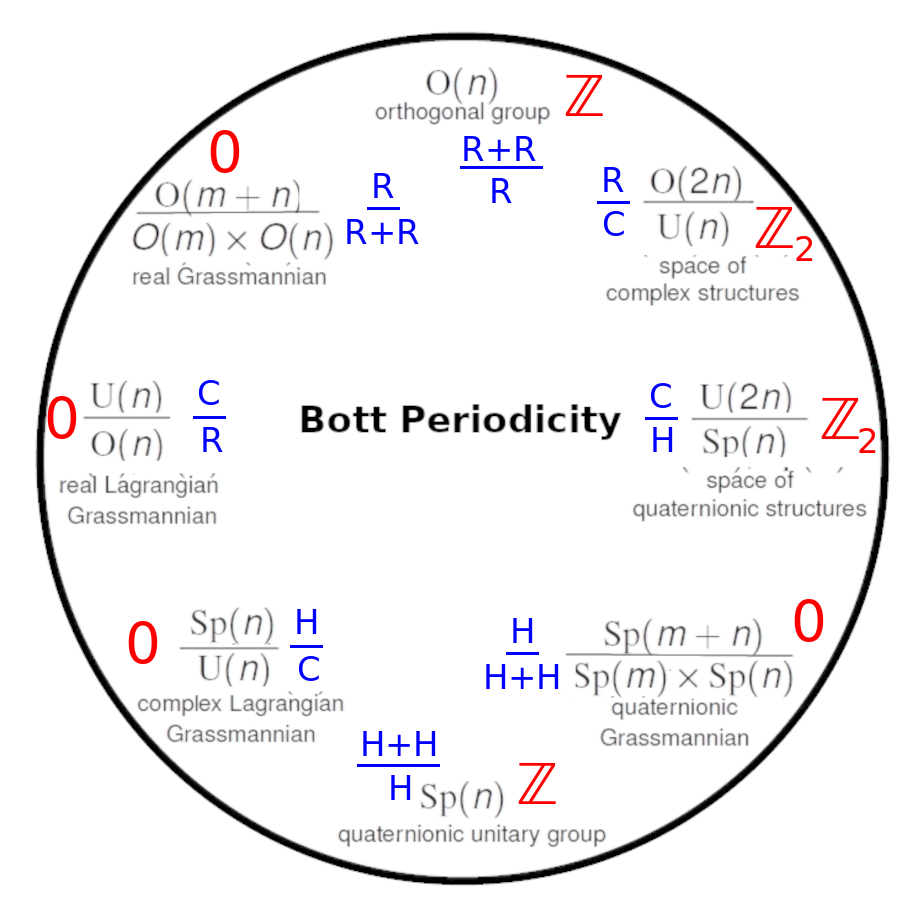
13:55 Symmetric spaces can be read off a chain of 8 embeddings amongst orthogonal, unitary and symplectic groups.

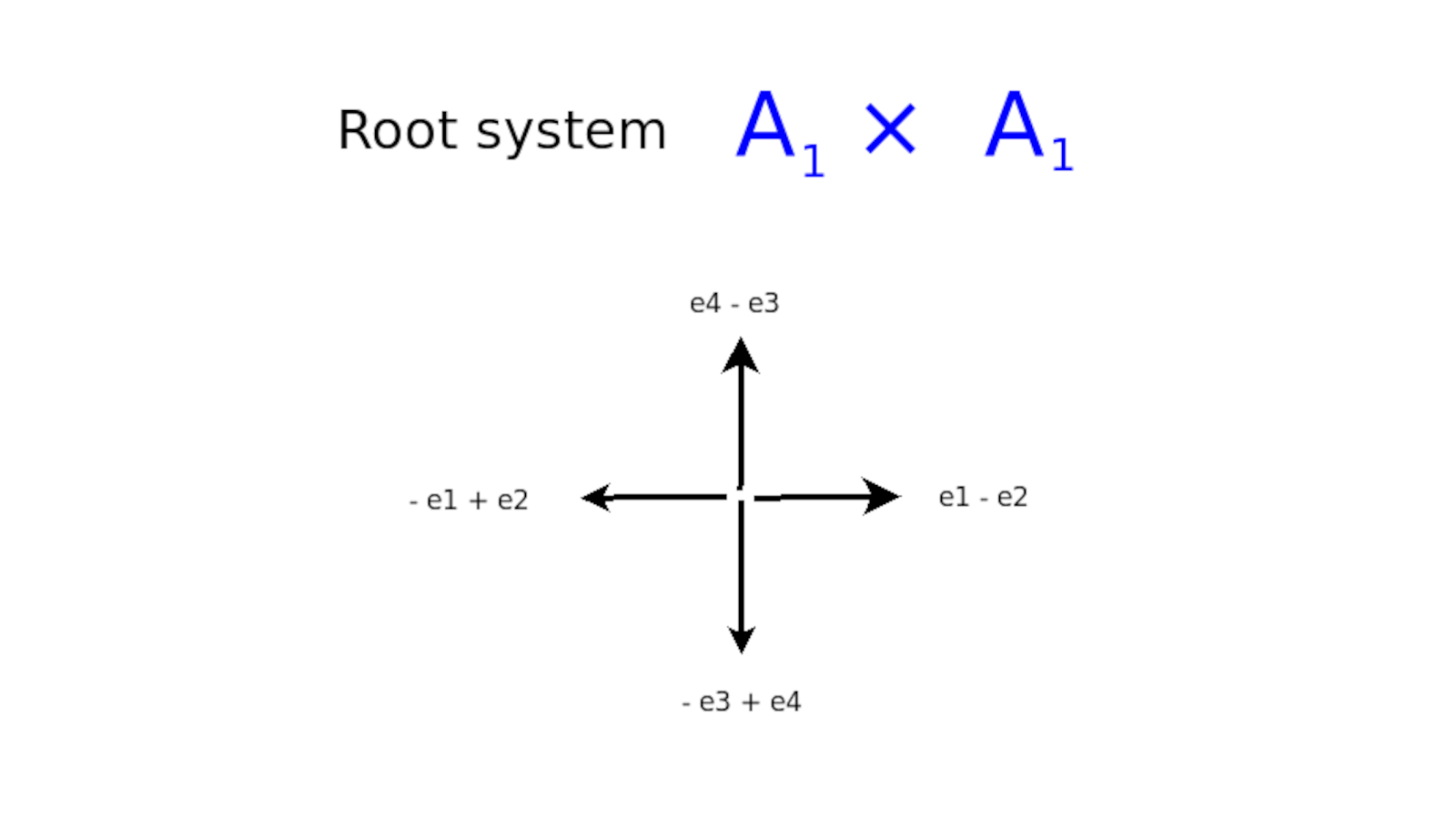
Bott periodicity has many manifestations. We'll talk about some of them. They're very metaphysical, which is kind of interesting, starting with those homotopy groups, spheres mapping to spheres. Maybe they somehow model perspectives. It's not crazy to think that. That's one clue but there are other clues we'll be looking at. For example, in physics, first of all, there are symmetric spaces. It turns out that one way to think about these orthogonal things like orthogonal groups is that there's a whole chain of these classical Lie groups and Lie families. It's not just rotations in the reals but it could be rotations in the complexes, which would be the unitary group, or rotations in the quaternions, which would be the symplectic group. You can change your norm in different ways so they have these embeddings. Orthogonal cross orthogonal is embedded in the orthogonal, which is embedded in the unitary, which is embedded in the simplectic, which is embedded in the simplectic cross simplectic, which is embedded back into the simplectic, which is embedded in the unitary, which is embedded in the orthogonal, which is embedded in the orthogonal cross orthogonal. So you get this eightfold embedding, which would all be sitting in that {$O(\infty)$} that we talked about. There's a simpler embedding that just focuses on the unitary. So {$U\times U$} is a subgroup of {$U$}.

John: It looks like {$U\times U$} is embedded in {$U$} but that's embedded in {$U\times $}. That looks like a kind of a bilateral embedding. Is that?

Andrius: I'm not exactly sure what this all means. I have to apologize. But I think it's like if {$U(n)\times U(n)$} is a subgroup in {$U(2n)$}. Then {$U(2n)$} is in {$U(2n)\times U(2n)$} among other things. So you would get that kind of chain but in {$O(\infty)$} you get them all. So then somehow you're focusing on {$O(\infty)$} or things like that, {$U(\infty)$}. You get these types of massive infinite structures.

16:25 Clifford algebras likewise manifest eightfold Bott Periodicity.

Now, a crucial thing is that (real) Clifford algebras, like the orthogonals, relate to the reals. The unitary group relates to the complex numbers. The symplectic group relates to the quaternions.

With real Clifford algebras, you get a similar type of embedding where {$\mathbb{R}\oplus \mathbb{R}$} is within {$\mathbb{R}$}, where the latter {$\mathbb{R}$} actually means {$2\times 2$} matrices in {$\mathbb{R}$}. Next we have {$\mathbb{C}$} which means {$2\times 2$} matrices in {$\mathbb{C}$} and next are {$2\times 2$} matrices in {$\mathbb{H}$}. Then you take those matrices and you add them to themselves to get {$\mathbb{H}\oplus\mathbb{H}$} in terms of {$2\times 2$} matrices of quaternions. And then those are in {$4\times 4$} matrices of quaternions.

In the case of the complex Clifford algebras, it is simpler. You just focus on the complex numbers.

This is a typical distinction between real numbers and complex numbers. If you have a vector space over complex numbers, then those complex numbers can reach into lots of places. They don't segregate {$+1$} and {$-1$}. Whereas in the case of a vector space over real numbers, then if you have something of the form have {$x^2=+1$} you can't get something of the form {$a^2x^2=-1$} if {$a$} is real. (Whereas if {$a=i$} then you could!)

18:05 Quotients of Lie groups define symmetric spaces. John Baez's talk. Definition of symmetric spaces.

What really matters for Bott periodicity though, it seems, are the quotients. You and I and others at Math4Wisdom saw the talk by John Baez on symmetric spaces. So they are these quotients. Those quotients are different symmetric spaces where you can take a space at any point and you have like a tangent vector and if you flip it to the negative tangent vector, that'll all work out okay. So that turns out to be a very strict type of symmetry. Now, those symmetries happen to relate to all different kinds of Hamiltonians.

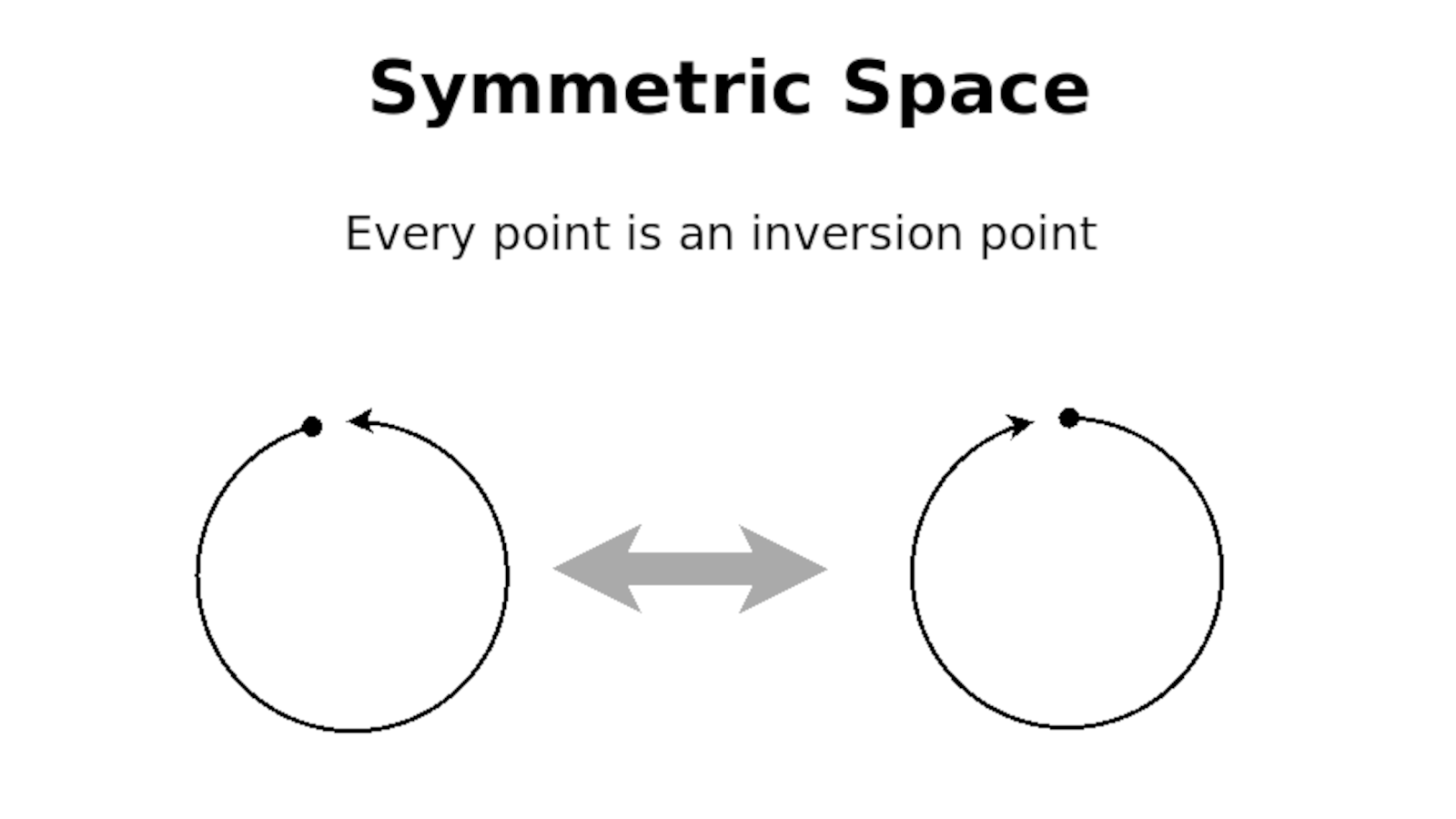
John: Can you repeat that symmetry one more time?

Andrius: I think the way it works, and I may get this wrong, but a symmetric space would be a space where at every point you look at the tangent vectors... so I guess it must be embedded in some space. If you have a point, if you have a space embedded in some ambient space, I suppose, and you have a tangent space and you pick a tangent Vector at that point then there will be an opposite. You can flip around all the vectors with their minus vectors and for the symmetric space it won't matter. Is that maybe like a local symmetry?

John: But don't all manifolds have that property?

Andrius: I'll have to check that out...

Andrius after checking: In defining a symmetric space, there are two things going on. One is that we're looking at an isometry at the point {$p$}. So there needs to exist an isometry such that on the tangent space at {$p$} it will act as minus the identity. So those two things are coming together. That's what I was missing and just to review for myself and others, see the definitions below:

So the picture that I was showing makes sense because there is an isometry that takes the circle to the circle by flipping it and for that particular isometry, a tangent vector pointing in one direction will get mapped to a tangent vector pointing in the opposite direction.

22:05 Clifford algebras make this more concrete.

So you have these symmetries, you have these quotients. I'll talk about Clifford algebras because my background is in algebraic combinatorics. I think maybe not just for me but for others as well, it is very hands on. It's something that can be explained to people who are at the community college level, potentially, if they're teachers or students who are really into math, using concepts like matrices and the binomial theorem. That's more like on my level.

22:50 Bott Periodicity is a statement in K-theory and vector bundles.

I've been studying some of the basics of algebraic topology but certainly I have a long way to go to understand it. Basically, Bott periodicity is a statement in K theory. When we were in graduate school at the University of California San Diego (I was there from 1986 to 1993), I overheard some professors talking in the library that K-theory is the most abstract, difficult branch of mathematics, the one that Grothendieck was inventing and Attiyah and Bott were using.

Bott periodicity is kind of like the foundation of K-theory, certainly in the complex numbers. K-theory has to do with vector bundles. They could be real vector bundles or complex vector bundles, how you are working with these entire systems of vector bundles. I guess that would be the kind of thing involved in studying symmetric spaces.

23:45 Grassmannian generalizes the binomial theorem, which generates the subsets of a set. Gaussian binomial coefficients count the subspaces of a vector space over a finite field.

If I was going to go into that, we'll see the binomial theorem. This notion of a Grassmannian is just like the binomial theorem in that it talks about defining choices. You can have {$\binom{n}{k}=\frac{n!}{(n-k)!k!}$}, which is the number of subsets of size {$k$} in a set of size {$n$}. You can do similar types of counting arguments with vector spaces. What are the ways of looking at a vector space that's broken up into a subspace? Let's say the vector space has dimension {$n$}, the subspace has dimension {$k$}, the complement has dimension {$n-k$}. What are the ways of doing that? Well, typically there are infinitely many ways. But let's say you're dealing with a finite field. Then all of a sudden those vector spaces have a finite number of elements and so you can actually do a counting exercise. If you switch from the binomial theorem to Gaussian binomial coefficients, where you replace let's say the number {$n$} with a polynomial in {$\mathbb{Q}$}, namely, {$1+q+q^2+\dots q^{n-1}$}, which has {$n$} terms, and if you substitute {$q=1$}, you would get back {$n$}. But instead of {$n$} you have this polynomial. It turns out that those polynomials divide each other just as the factorials in {$\binom{n}{k}=\frac{n!}{k!(n-k)!}$} divide each other.

25:35 Grassmannian are manifolds of the subspaces of a vector space. Bott Periodicity organizes the different flavors of Grassmannians.

What the Grassmannian does, it says let's look at the manifold you would get by looking at these quotients over the reals. That would be the real Grassmannian and it's written out here {$\frac{O(m+n)}{O(m)\times O(n)}$}.

It turns out you can do all these different flavors of Grassmannians. So instead of real vector subspaces of real vector spaces, it could be the real vector subspaces of complex vector spaces. Alternatively, what are the complexified real vector subspaces in a real vector space? (I don't understand this here!) If they're complexified that means that they have to be harmonious with regard to the structure that you could put on that would make them complex. So you get eight different flavors of Grassmannian. Somehow I think that orthogonal group of itself is counting something very much like the binomial theorem. The symplectic group likewise, I guess.

26:50 The binomial theorem applies to generators of Clifford algebras. I think the pattern of groups {$\mathbb{Z}_2, \mathbb{Z}_2, 0, \mathbb{Z}, 0, 0, 0, \mathbb{Z}$}, refers to metaphysical flavors of choices.

That's the approach I would take if I was trying to understand this. I would use the binomial theorem, which we'll show is really at the heart of Clifford algebras. I would look at the Grassmannians, the symmetric spaces, and then maybe try to understand a little bit about vector bundles. It's really a bit optional as what we're doing for Math 4 Wisdom is just trying to understand how could this pattern match over. Because these are just kind of like signatures or symptoms of that pattern {$\mathbb{Z}_2, \mathbb{Z}_2, 0, \mathbb{Z}, 0, 0, 0, \mathbb{Z}$}. It's just a little indicative pattern. It's not saying the entire structure of what's going on there. There's a deeper thing going on there. So I'm trying to figure out how to read that. The metaphysical point being that different kinds of choices, different flavors of choices, that's metaphysical.

27:50 Imagine an 8-track mind. Each choice is not independent because it affects how many more choices the mind can make.

To expand on that, what it seems to be is, we like to think that choices are independent. But imagine if they weren't. Imagine if the second choice you make is different than the first choice. The reason being that your brain is limited. Let's say your brain is like an eight trackk mind, but you only see the tracks you're using. So sometimes you have a one track mind when you're thinking about everything but then you'll have a two track mind when you think about existence because you need to be able to ask, well maybe you know this television exists or it doesn't, but if it does then it does. So it's like free will and fate. But then you might need a three track mind learning by taking a stand, falling through and reflecting, and you'll have five tracks left over that you're not even worried about. Basically, when you get up to the eighth track, the whole thing collapses. So it's really maybe a seven track mind and then you'll have a zero track for when you're not using your mind at all, which is how you would model God.

28:45 Neurologically, the brain may have a map of this eightfold mind.

Neurologically, if you're a materialist, you'd say the brain has a map of the body. When I pick up a hammer, all of a sudden I feel like my arm got longer. Likewise, the brain should have a map of the mind, and this would be the map of the mind. The brain would be able to say, "You have no perspectives", which would imply that you're doing something equivalent to contemplating God. But if you have one perspective, you're contemplating everything.

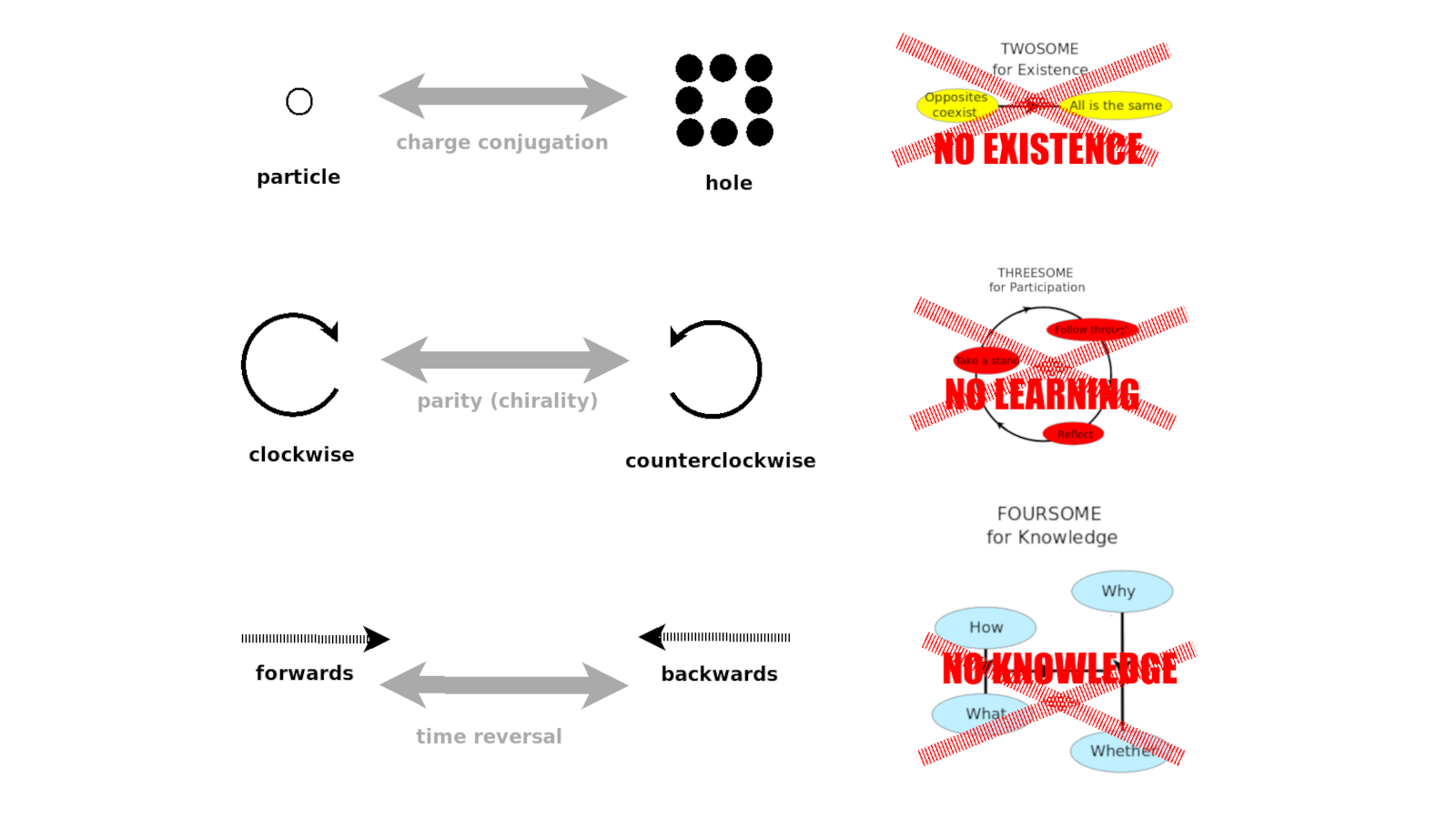
29:20 There is a two-fold unitary Bott perioidicity. 8+2=10. Topological insulators have a Tenfold Way relevant for quantum computing. Classification of spaces of Hamiltonians.

There is another metaphysical thing that comes up. First of all, there's a simpler two-fold Bott periodicity that goes back and forth between {$U(n)$} and {$\frac{U(m+n)}{U(m)\times U(n)}$} in the complex world. It's complex vector space bundles or complex Clifford algebras. Now {$8+2=10$} and in physics, in the study of topological insulators (which can possibly be two dimensional with a one-dimensional boundary), where you have an insulator and an electromagnetic world on top of that. You can have different manifolds or structures where the physical properties become different. Basically, the laws of physics change depending on how you insulate something, how you construct the space. It'll change in three kinds of ways: the notion of time reversal could be there or not, charge conjugation could be there or not, and parity could be there or not. These are the components of CPT symmetry which is a very important symmetry. You can break one or perhaps two of those symmetries but you can't break all three of them. All three work together.

These are very metaphysical notions. If there's time reversal, then something can become, but if there's no time reversal, then there's no becoming, there's no "how". This brings to mind the foursome for levels of knowledge: Whether, What, How, Why.

Charge conjugation is, in my understanding, saying that if you have a sea of particles and in that sea you have some kind of hole where a particle is missing, is that hole distinguishable from an anti-particle? In some situations it would be, and in some situations it wouldn't be. That's like talking about existence or being. That hole, does it exist or does it not? If it's like an antiparticle, maybe existence means one thing, and if it's not like an anti particle, then maybe it means another thing. If it's not like an antiparticle, then maybe it means just a hole, so it doesn't exist.

With parity you have three dimensions. I don't know exactly how it works. If you flip one dimension or all three you get a different handedness, left or right. This may relate to the three-cycle for learning, which turns in one direction but not the other. That's encouraging to think there's some kind of a connection here.

John: When you say topological insulator are you actually talking about a two-dimensional surface embedded in our space or are you talking about something more abstract?

I'm not qualified to say but I think it's just very simple it's like two-dimensional [with a one-dimensonal boundary, or three-dimensional with a two-dimensional boundary].

John: That's kind of curious. Do these things actually exist or are they just constructs?

At this point, I think they exist. [Some but not all of these forms of matter have been experimentally observed.] In fact, this is very important for quantum computing because you're creating different environments. I'm not sure, but I think that all [actually, some] of these exotic matters have been demonstrated. This is actually a classification of exotic matter, in a certain sense. There may be more complicated things going on but there is a sense this is very real physically.

34:00 Why are there 4 classical Lie families?

I didn't know all these things when I started. But one thing that was encouraging when I did start was the role of Lie theory. We're old friends and when you started studying Griffith's book in quantum physics about almost three years ago, I was glad to join you because you have great physical insight and I wanted to get some physical intuition regarding Lie Theory.

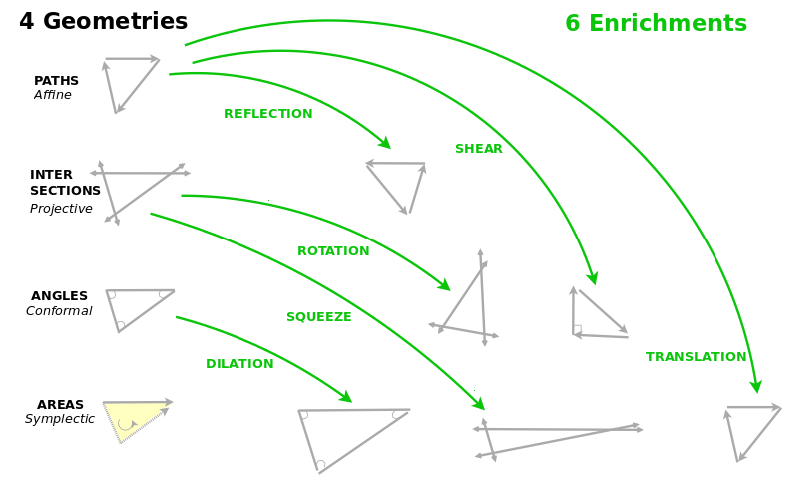
In Wondrous Wisdom, I separately thought, based on my study of ways of figuring things out in mathematics (and I'm making a series of videos on that), there should be four geometries. So I was very intrigued that in Lie Theory there are four classical families (even orthogonal, odd orthogonal, unitary, symplectic) and maybe each of them establishes a different geometry.

Certainly, each of them defines a different type of rotation. So that's a hypothesis that I'm working on.

35:00 How to organize all of math and its branches? Lie theory links algebra and analysis.

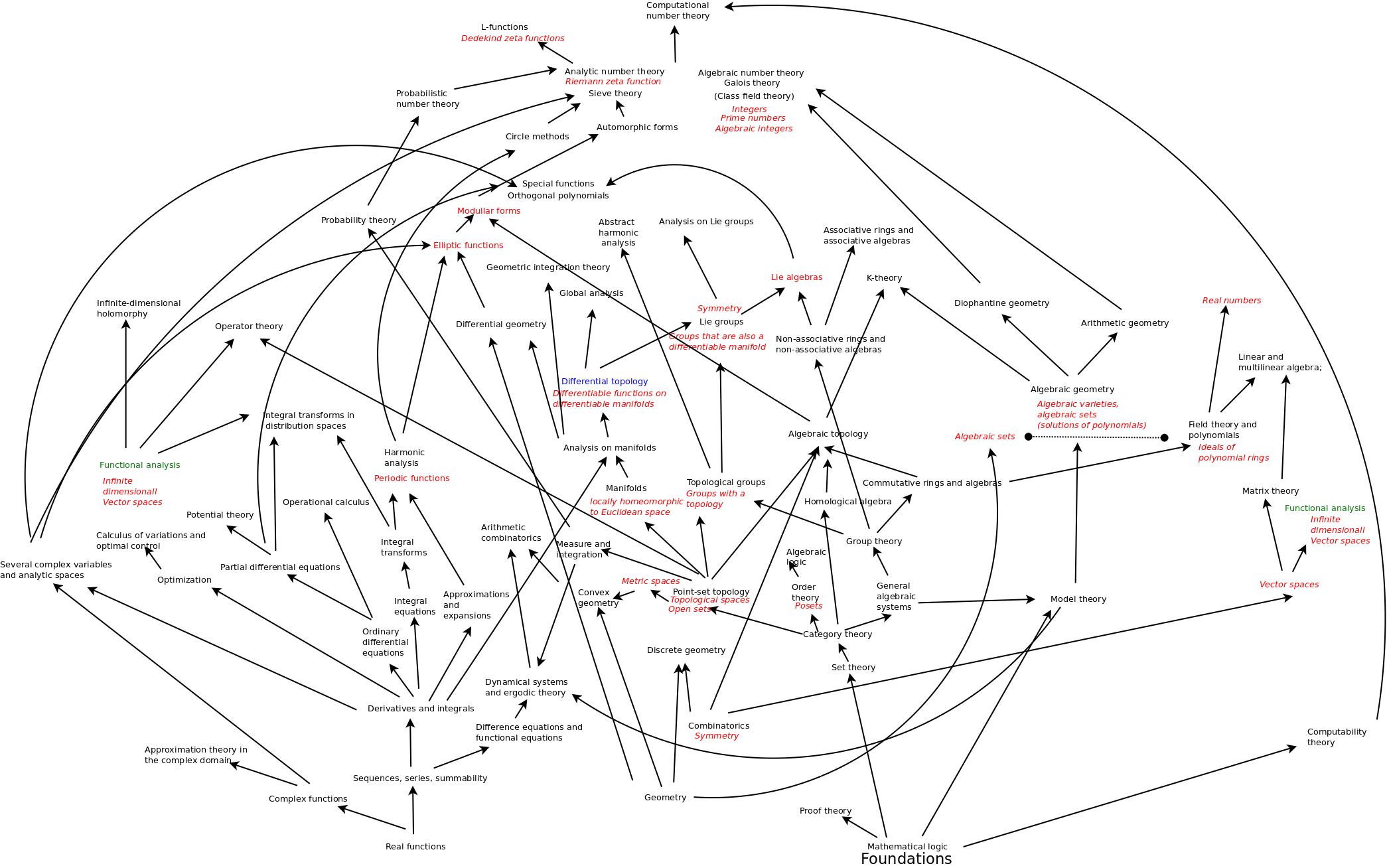
One of the things I looked at was that it would be a great demonstration that Wondrous Wisdom is truly real if I could organize all of mathematics and show that I have the skeleton key to do that. One of the things I did to try to get a grip on the big picture of mathematics was that I looked at the system of classification of articles in math journals. You can have a article in differential topology, harmonic analysis, elliptic functions, modular forms, K theory and then the question is, which of these disciplines or branches depends on which other branches? Thus you can draw a map of these dependencies. At the bottom you'll have things like you geometry, real functions, combinatorics, mathematical logic but at the top you would have number theory. It's not clear know how good this map is. The one thing I did learn was that there seem to be two wings. One is algebra and the other is analysis. They seem to come together in geometry, but especially, Lie groups, Lie algebras, is where they are intermeshing. It's the algebra of continuity, I guess is one way to think about it. So this is the heart of mathematics. There are some exceptional Lie groups and algebras. But more interesting to me are the four infinite families and how to understand them.

36:50 What are the symmetries of math itself? Root systems of classical Lie families relate counting forwards and backwards.

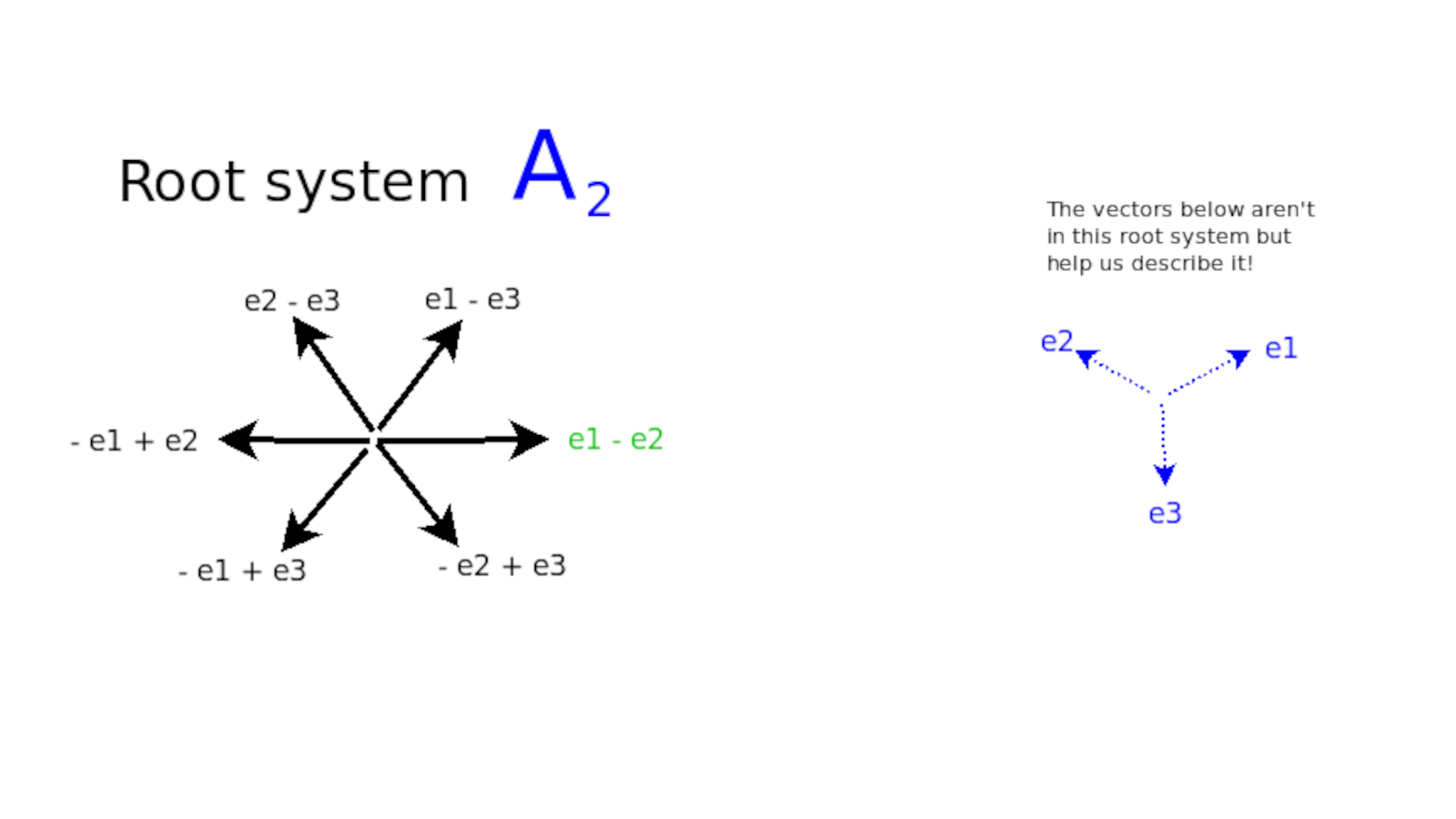
I'm looking at the symmetries inherent in math itself. Why are there four classical families of Lie groups and Lie algebras? I tried to chase down this question and I think I'm pretty satisfied with the answer I have. If you look at the root systems of the Lie algebras, then you'll see that most of the roots are of the same form, {$x_i-x_j$}, as you would have with the simplexes. In fact, in the unitary case, that's what they are.

John: Can you remind me of root systems again?

If you have a Lie group, then it's a continuous group, and it is very much determined by what's happening at any point locally. It's a continuous group and so it has a tangent space. That tangent space is multi-dimensional and it's described by the Lie algebra. The skeleton for that Lie algebra would be the root system. These root systems are extremely symmetrical. They are very tight systems. In the case of {$A_2$}, there are six vectors separated by 60 degrees. That is the root system for {$\frak{su}(3)$}.

John: Okay, are they related to the Lie bracket?

Yes. A Lie algebra is building on the Lie bracket. When you have a Lee algebra you don't really have multiplication. You have instead the Lie bracket operation which is saying {$[X,Y]=XY-YX$}, if you were able to write that Lie algebra, as you typically can, as a matrix algebra. But {$XY$} wouldn't make sense by itself and {$-YX$} wouldn't make itself but the bracket {$[X,Y]$} makes sense in this concept of Lie algebra. That's the logic of it and it ends up being the logic about these roots. And there are very few possibilities. Basically, you get chains such as {$x_4-x_3, x_3 - x_2, x_2-x_1$} and you could do plus or minus these, and those are your [simple] roots. What I'm saying as a combinatorialist is that this is encoding counting. If you count {$1,2,3,4,5 \dots$}, how would you encode that? {$x_2-x_1$} encodes the idea that when you have {$1$} you will go to {$2$}. Likewise, {$x_3-x_2$} encodes going from {$2$} to {$3$}. Thus we are counting up to {$n$}.

The crucial thing about counting is that it has a symmetry that when you count forwards you can also count backwards. So it turns out that there are three other kinds of symmetries in counting that you could have. What you do is you add a widget at the end. There are three kinds of widgets and they give you three three other systems. This comes up in practical life for historians. They want to be able to count forwards and backwards as far as they like. But how do you have a year where you start from? Because you can't start from {$-\infty$}. So then you will need to be able to count backwards. How do you connect those two counting systems? Probably most people don't even think about it. They don't really know. But you have to make a choice and so there are three possible choices. One choice would be to add a zero and then you would count {$\dots -2, -1, 0, 1, 2\dots $}. So then instead of counting forwards {$1, 2, 3$} and separately counting backwards {$-1, -2, -3$}, as we do in the unitary case, based on the complex norm, you can connect these two systems by adding {$0$}. How would you do that? You add a root {$x_1 - x_0$} where {$x_0=0$}. So it's like you're counting from {$0$} to {$1$} with {$x_1-x_0 = x_1$}. That will work in both directions as we count from {$-1$} to {$0$} with {$x_0-x_1=-x_1$}. But this will have huge consequences because it's like ripping open the floorboards and getting down to the foundation of the building. For if {$x_1$} is a root, then you can add this to {$x_2-x_1$} and so {$x_2$} is a root as well, and {$x_3$} likewise. Now {$x_1$} and {$x_2$} are independent, separated by 90 degrees. Whereas {$x_1$} will be related to {$x_2-x_1$} by 90+45=135 degrees. This is the end of the chain in the Dynkin diagram. But {$x_2-x_1$} and {$x_3-x_2$} are related by 120 degrees and that is the case all the way down the chain.

You can link counting forwards and counting backwards in another way. You could fuse the ends so that instead of adding a {$0$} you could simply identify {$1$} and {$-1$}, as if that was the same year for a historian, an internal zero, counting {$\dots -3,-2,-1=1,2,3\dots$}, which is to say, from {$-2$} straight to {$1$}. The root is {$x_1-(-x_2)=x_1+x_2$}.

Then a third way is if you just fold it, without any zero, counting {$\dots -3, -2, -1, 1, 2, 3\dots$}. The root is {$x_1-(-x_1)=2x_1$}.

So if you work out the algebra that's what it seems to be encoding. For me, that's an explanation of what's going on here which is cognitive. But I'm venturing away from Bott periodicity so I want to move on. Any thoughts on that?

John: So these root systems, what kind of algebraic structure do they have?

To be fair, I've forgotten everything. This has been several years. So I'm just trying to say that this is the answer. But the point is is that there is this answer here saying that there's a symmetry in counting between backwards and forwards.

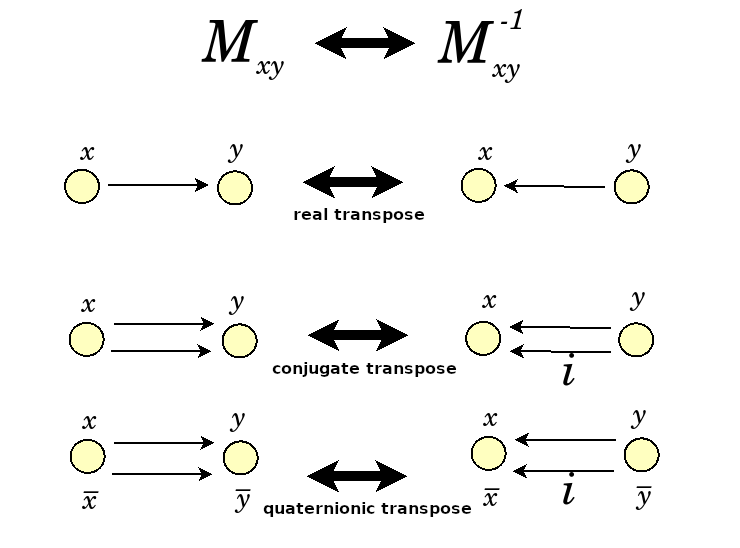
44:20 Inverse matrices expressed by transposes, conjugate transposes, quaternionic transposes. Symmetries of math itself.

This is the kind of symmetry that's at the heart of mathematics, where math is described in terms of math right. These are the things that we take for granted in math. Here's another one. When you have a matrix in these Lie groups, and you look at the inverses. Normally, you would have to calculate something very complicated with Cramer's rule. You'd have to take determinants over determinants. But in the case of rotations, it's very easy to take the inverse. You just do the transpose. Now, you have three different types of transpose. So instead of {$x\rightarrow y$} which would be encoded {$M_{xy}$}, the transpose would be {$M_{yx}$} encoding {$y\rightarrow x$}.

You could also be encoding the conjugate transpose, dealing with complex numbers, in which case you'd have to worry about two arrows. You could encode the quaternionic transpose using four arrows.

What I really wanted to talk about is the progress I'm trying to make to understand Bott periodicity. But the point of this was that what Bott periodicity I think is doing is that it's saying that in a matrix, which is a way of looking at external relationships in math, as with an arrow in category theory, then we can consider what are the possible symmetries inherent in a matrix. The idea is that it's really about {$2\times 2$} matrices and what you can do with them. There are only so many symmetries that you can get playing with {$2\times 2$} matrices and in the end you'll just get back to where you started. I imagine folding up those matrices in all the different ways and then running out of possibilities. That's what this is about. That was a long tangent!

46:30 How to calculate the pattern for Bott Periodicity? Paper by Attiyah, Bott, Shapiro. Exposition by Dexter Chua. Book Fibre Bundles by Dave Husemoller.

I'm really focusing now on trying to understand how to calculate the series {$\mathbb{Z},\mathbb{Z}_2,\mathbb{Z}_2,0,\mathbb{Z},0,0,0$}. The basic answer is given by Attiyah, Bott and Shapiro in a paper that they published in 1963 called Clifford modules. So this was four years after Bott figured out his periodicity, and because they realized that Clifford modules have this same periodicity, they tried to link that up. The first paper showed that it is the same periodicity but didn't explain why. So in subsequent papers they found a deeper reason why these patterns match up. Dexter Chua was a Harvard grad student who wrote this up as Clifford Algebras and Bott Periodicity. His first chapter was helpful for me as a simpler explanation of this. There's a book by Dale Husemoller on Fibre Bundles which goes in much more detail. It's even more helpful, but it's still very hard for me.

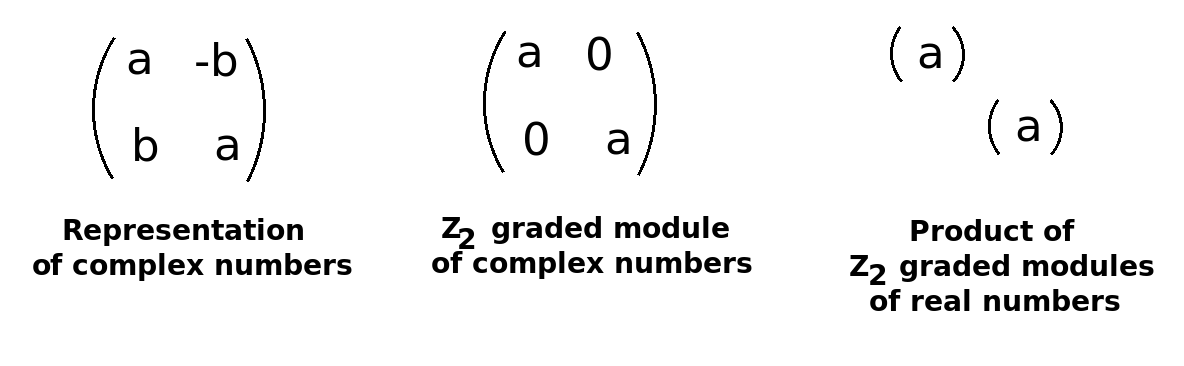
47:35 How matrices fit together. {$\mathbb{Z}_2$} signifies that a {$2x2$} representation of complex numbers contains two {$1x1$} representations of real numbers. Grothendieck groups express this obtusely.

The gist is this: Where do you get {$\mathbb{Z}_2$}? Where do you get {$\mathbb{Z}$}? Where do you get {$0$} from? Basically, it's how matrices can fit together. In the practical sense, it's probably something almost trivial. For example, here's the way you would represent complex numbers with matrices as when you gave your talk on complex numbers. You have {$a$} on the diagonal and {$-b$} and {$b$} on the anti-diagonal. Suppose that you have this but you're only going to look at the real component. One way to argue that is to say, the complex part is odd. It's the first generator. {$1$} is an odd number, so we're going to ignore it. We're just going to look at the subalgebra that's the reals. When you do that, all of a sudden you lose these anti-diagonal elements. You get a breakdown. This was an irreducible representation. But now this is two copies of a reducible representation in the reals. So you're getting a product in the reals. What was an irreducible from the point of view of the complex numbers, from the point of view of the real numbers is two copies of an irreducible representations. So that's {$\mathbb{Z}_2$}. That's what {$\mathbb{Z}_2$} is saying.

They make it more complicated. They say, let's take the irreducible representation of complex numbers (there's only one of them!) but let's imagine the monoid of all the representations of complex numbers up to isomorphism. So instead of one, you would be able to have as many copies of this as you like. So that would be all the natural numbers. Then you could say, let's do a Grothendieck construction, where we would make a group out of that. So then you just presume that all of these have inverses. And then you would show that the monoid can be thought of as a group. That group would be {$\mathbb{Z}$}. So this would be {$\mathbb{Z}$}. When you map this into that you would get two copies of {$\mathbb{Z}$} mapping into {$\mathbb{Z}$}. Then {$\frac{\mathbb{Z}}{2\mathbb{Z}}\cong\mathbb{Z}_2$}. That there's a very complicated way just to say what was very simple here, {$2=2\times 1$}. Any questions about that?

John: It seems like just playing around with inconsequentials. But obviously they're talking about a more general context for that whole circle of ideas.

It's not clear. In the case of Clifford algebra, they use a super abstract machinery. But when you ask why, when you calculate {$\mathbb{Z}_2$}, the answer is well it's just {$2=2\times 1$}.

51:00 {$\mathbb{Z}$} arises because {$\mathbb{R}\oplus\mathbb{R}$} has two irreducible representations.

That's one of the points of what we're doing, which is to learn how to talk about this in simple ways. In the other case, Wedderburn's theorem says that a matrix algebra of {$\mathbb{R}$} or {$\mathbb{C}$} or {$\mathbb{H}$} has only one irreducible representation, the natural representation. Thus the math can be very complicated yet in the end, the answer is going to be trivial. There's only one irreducible representation in these cases.

[At this point I would like to say that {$\mathbb{R}\oplus\mathbb{R}$} has two irreducible representations, and consequently, they will generate the group {$\mathbb{Z}\oplus\mathbb{Z}$} and then modding out by {$\mathbb{Z}$} yields {$\mathbb{Z}$}. I suspect that happens but I have not yet been able to work out the calculations yet! I am working on it but I appreciate any help you may give!] ... So it's kind of like {$2-1=1$}. I have to work out on the math.

52:40 {$0$} arises when matrices have the same size.

it's just a mess trying to understand this but that's really you know that's what will it be and then

The trivial group {$0$} is just saying that when you have Clifford algebras and you're comparing them, if the matrices are the same size, then you get {$0$}. So there's this huge deal trying to understand that pattern. But that is the source of the pattern right there that I'm still working to understand.

53:15 Overviewing the eightfold pattern.

John: So I'm not quite sure I got the gist of this pattern here.

So this is the pattern back here, going around this clock. So the pattern would be like this:

Complex numbers compared to the real numbers will have this {$\mathbb{Z}_2$}.
Quaternions compared to the complex numbers will yields {$\mathbb{Z}_2$}.
If you have {$\mathbb{H}\oplus\mathbb{H}$} compared to {$\mathbb{H}$}, they are using the same size matrices, and this yields {$0$}.
If you have {$2\times 2$} matrices of {$\mathbb{H}$} compared with the split biquaternions {$\mathbb{H}\oplus\mathbb{H}$}...

[Here I am floundering! I need to work on this further!] This has only one irreducible representation so we will end up with {$\mathbb{Z}\oplus\mathbb{Z}/\mathbb{Z}\cong\mathbb{Z}$}

When you go further, what's going to happen is that, instead of matrices of quaternions, you'll have matrices of complex numbers, but the size of their matrix representations in terms of real numbers will stay the same. This gives us {$0$}.
Similarly, when you go from complex numbers back to the real numbers, then the size of the matrix representations in terms of real numbers will stay the same, again giving us {$0$}.

55:00 Clifford algebra extends the binomial theorem.

Why don't I go further down it'll be maybe a little bit more helpful to see what's up. So we have to just be a little bit more clear what is a Clifford algebra. They extend the binomial theorem. You have the real numbers and you add generators. Let's say when you square a generator {$e_i$} you get {$e_i^2=-1$}.

The first generator {$e_1$} will just give you {$\mathbb{C}$. You'll have {$1, e_1$}.

The second generator, though, if you have {$e_1$} and {$e_2$}, then you're allowed to multiply them together. That'll give you a third basis element {$e_1e_2$}. So if {$e_1=i$}, {$e_2=j$}, then {$e_1e_2=k$}. So you get the four basis elements of the quaternions but you need only two generators to construct that.

Then for {$\mathbb{H}\oplus\mathbb{H}$} you need a third generator {$e_3$}. You'll get pairs of generators {$e_1e_2, e_1e_3, e_2e_3$} and you'll have the product of all three {$e_1e_2e_3$}. If you multiply more together, then the square of a generator {$e_i^2=-1$}, so you'll not get more possibilities.

At each level you can continue and with {$k$} generators you'll get {$2^k$} basis elements. The generator squares to {$-1$} but it could also square to {$+1$} or {$0$}. The zero case is degenerate and it is actually very important for the Grassmannian, the external algebra.

57:00 Binomial theorem here is asymmetric, thus the pseudoscalar is key. Anticommutativity.

John: So you're saying that that this is a Clifford algebra. So the real numbers, complex numbers, quaternions fit in this chain of Clifford algebras.

The question is how do you calculate them. They're easy to define. It's basically the binomial theorem, as in the video I created, Binomial Theorem is a Portal to Your Mind, because you're deciding whether to include a generator or not. Here in this diagram, you're making three choices, and here you only chose to include one of them, here you chose to include two of them, here you chose to include all three, here you chose to include none of them. So you also get this very important distinction between choosing none of them, which would give you the identity, and choosing all of them, which functions as a what's called a pseudoscalar. This is very important in terms of the character of the patterns that are unfolding. THe other thing that's very important for the structure of the Clifford algebra is that {$e_ie_j=-e_je_i$}, so there's this an ordering phenomenon where {$e_1e_2$} can be taken as going from left to right but if you understand it to go from right to left, then you would have to switch it to negative to read it from left to right. You need to introduce a negative sign and that's what makes it interesting.

58:25 Calculating Clifford algebras as matrix algebras using recursion relations.

So how do we figure out this {$\mathbb{H}\oplus\mathbb{H}$}? You use these recurrence formulas

{$\textrm{Cl}_{p+2,q}(\mathbf{R}) = \mathrm{M}_2(\mathbf{R})\otimes \textrm{Cl}_{q,p}(\mathbf{R}) $}
{$\textrm{Cl}_{p+1,q+1}(\mathbf{R}) = \mathrm{M}_2(\mathbf{R})\otimes \textrm{Cl}_{p,q}(\mathbf{R}) $}
{$\textrm{Cl}_{p,q+2}(\mathbf{R}) = \mathbf{H}\otimes \textrm{Cl}_{q,p}(\mathbf{R}) $}

applying them to the simplest cases, namely, {$\mathbb{R}$} and {$\mathbb{C}$} and {$\mathbb{R}\oplus\mathbb{R}$}. The latter is generated by the generator {$e_1$} where {$e_1^2=+1$}. If you have two generators {$e_1$}, {$e_2$}, where both square to {$+1$}, then {$\textrm{Cl}_{2,0}(\mathbf{R})= \mathrm{M}_2(\mathbf{R})\otimes \textrm{Cl}_{0,0}(\mathbf{R}) = \mathrm{M}_2(\mathbf{R})\otimes\mathbf{R} = \mathrm{M}_2(\mathbf{R})$}.

59:10 2x2 real matrices have two generators which square to +1 but their product squares to -1.

A very interesting thing happens in this case. If you multiply together {$e_1e_2$} and you square that, then you have {$(e_1e_2)^2=e_1e_2e_1e_2 = -e_1e_1e_2e_2 =-1$}.

1:00:10 If one generator squares to +1 and the other to -1, then their product squares to -1. This also defines 2x2 matrices.

Whereas if you have one generator {$e_1^2=+1$} that squares to {$+1$} and another generator {$e_2^2=-1$} that squares to {$-1$}, then note that the product squares to {$+1$}: {$(e_1e_2)^2=e_1e_2e_1e_2=-e_1^2e_2^2=+1$}. In each case, it turns out to give you the same algebra, {$2\times 2$} matrices {$\mathrm{M}_2(\mathbf{R})$}, but they are graded differently.

John: What do you mean by the algebra will be the same...?

1:00:50 Grading distinguishes odd and even basis elements.

The grading is very important. The grading is deciding the levels, what to assign {$e_1$} to, what to assign {$e_1e_2$} to, going down the diagonals. You have {$1$}, then you have {$e_1$} or {$e_2$}, then you have both {$e_1e_2$}, and you can go on, {$e_1e_2e_3$}, {$e_1e_2e_3e_4$}, with the power of the term yielding a natural grading. We're going to be looking at grading in terms of even and odd powers. This diagonal of {$1$}s is trivially even, a single generator is odd, but the product of two generators is even, but the product of three generators is odd. So going across the diagonals we switch odd or even.

1:02:00 Keep track of generators that square to +1 or -1. Recursion relations tensor with 2x2 real matrices or with quaternions.

A Clifford algebra is more than just an algebra because a Clifford algebra identifies the generators. But if you ignore the identifications, then this ends up being just an algebra. Building it up, you start with {$\mathbb{R}$}, then you can choose to construct {$\mathbb{R}\otimes\mathbb{R}$} or {$\mathbb{C}$} depending on whether your generator squares to {$+1$} or {$-1$}. Then, adding another generator, it's either {$\mathbb{H}$} if both generators square to {$-1$}, or if you choose one squaring to {$+1$} and the other squaring to {$-1$}, that that yields {$2\times 2$} matrices {$\mathrm{M}_2(\mathbb{R})$}, and if they both square to {$+1$}, then you also get {$\mathrm{M}_2(\mathbb{R})$}. Once you know that, then the rest you can do by tensoring.

In the case of complex Clifford algebras, you don't distinguish between generators that square to {$+1$} or {$-1$} because you have scalars that are complex numbers and so that distinction doesn't lead to anything. It's just the number of generators that determines the complex Clifford algebra. But in the case of real Clifford algebras, it does matter, so you have to keep track of both. So if you have {$\textrm{Cl}_{p+2,q}(\mathbf{R})$}, then there are {$p+2$} generators that square to {$+1$} and {$q$} that square to {$-1$}. When you add two generators that square to {$+1$}, those two contribute {$2\times 2$} matrices {$\mathrm{M}_2(\mathbb{R})$} which by the recurrence relation are tensored with \textrm{Cl}_{q,p}(\mathbf{R}), which came from the other side of the construction, flipping {$p$} and {$q$} around. If you're adding one generator of each kind, then you tensor by the {$2\times 2$} matrices {$\mathrm{M}_2(\mathbb{R})$}. If you're adding two generators that square to {$-1$}, as we'll be doing to get {$\mathbb{H}\oplus\mathbb{H}$},s then you tensor by the quaternions {$\mathbb{H}$}, and again the {$q$} and {$p$} are switched around.

There are homomorphisms that manifest each of these recurrence relations. I have to write them down and work with them. But basically they give you these constructions, where you're braiding back and forth.

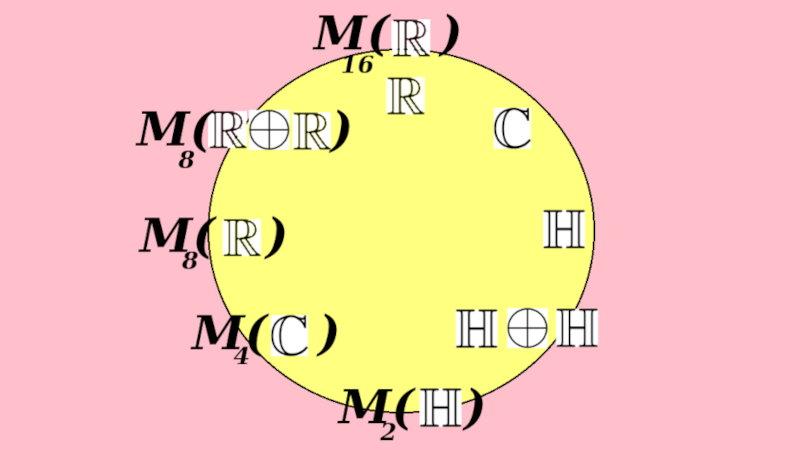
Let's say we start with {$\textrm{Cl}_{0,0}=\mathbb{R}$}, so then {$\textrm{Cl}_{0,2}=\mathbb{H}\otimes\mathbb{R}=\mathbb{H}$} equals the quaternions. Then {$\textrm{Cl}_{0,4}=\mathbb{H}\otimes\mathrm{M}_2(\mathbb{R})\otimes\mathbb{R}\cong\mathrm{M}_2(\mathbb{H})$}. And {$\textrm{Cl}_{0,6}=\mathbb{H}\otimes\mathrm{M}_2(\mathbb{R})\otimes\mathbb{H}\otimes\mathbb{R}\cong\mathrm{M}_4(\mathbb{H})$} are {$4\times 4$} matrices in the quaternions. And then {$\textrm{Cl}_{0,8}=\mathrm{M}_{16}(\mathbb{R})$}.

1:05:00 Morita equivalence. Categorically, 16x16 matrices in R are indistinguishable from R itself.

Now it turns out by Marita equivalence, once you get to {$16\times 16$} matrices in {$\mathbb{R}$}, if you look at them from a category theory point of view, if you look at the representation theory of that, the homomorphisms that go between these matrices, it's the same category as you would have for {$\mathbb{R}$}. It looks the same, basically, so from a certain point of view this is indistinguishable from {$\mathbb{R}$} structurally. From the outside you can see the difference but if you're inside the structure you can't tell the difference because they're isomorphic. So that's where the periodicity comes in here in the Clifford world.

You can also start with {$\textrm{Cl}_{0,1}=\mathbb{C}$} and then you'll get {$\textrm{Cl}_{0,3}\cong\mathbb{H}\oplus\mathbb{H}$} and {$\textrm{Cl}_{0,5}\cong\mathrm{M}_4(\mathbb{C})$} and {$\textrm{Cl}_{0,7}\cong\mathbb{R}\oplus\mathbb{R}$}.

So this is the kind of thing that's going now from the point of view of Marita equivalence. It turns out that if you're working with {$4x4$} matrices in {$\mathbb{C}$}, it's the same as if you working with just {$\mathbb{C}$}. I think that's the case.

1:06:10 4 generators that square to -1 yields the same 2x2 matrices of quaternions as do 4 generators that square to +1.

So another way to look at Bott periodicity is if you have all four generators squaring to {$-1$}, that gives you {$2\times 2$} matrices in the quaternions, {$\mathrm{M}_2(\mathbb{H})$}, but if you have all four generators squaring to {$+1$}, that also gives you {$\mathrm{M}_2(\mathbb{H})$}. So you end up in the same place, and {$+4$} and {$-4$} are separated by {$8$}. So this is where I should stop.

1:06:35 Groups {$A_k$} in terms of the inclusion map for Clifford algebras, and the reverse map for their even graded representations.

Here's the formula that I need to explain. So these groups which we call {$A_k$}, which are, in practice, {$\mathbb{Z}_2$} or {$\mathbb{Z}$} or {$0$}, are constructed as follows. You take the Clifford algebra {$\textrm{Cl}_{0,k}$} and you look at the even graded representations. So that would be saying look at the matrix representation but ignore all the odd powers of generators. We did that earlier, we said ignore the imaginary numbers, which is the first generator, thus an odd power of generators. Then this will break down so the even graded modules will be these blocks separately. You have this concept of even graded module where you keep things separate. This relates very much to spin because spin has to do with the even parts of Clifford algebras. Then what you have to do, you have this inclusion map {$i$} which includes the {$k$}-th Clifford algebra {$\textrm{Cl}_{0,k}$} into the {$k+1$}-st {$\textrm{Cl}_{0,k+1}$}, where all the generators square to {$-1$}.

So having this inclusion, how do you work backwards? Well, if you have an even graded module of a Clifford algebra {$\textrm{Cl}_{0,k+1}$} that's bigger by one generator, then when you think backwards, you're including a smaller Clifford algebra {$\textrm{Cl}_{0,k}$} into the bigger one just by thinking of it as a subalgebra. It turns out with representations you can go backwards from the bigger one to the smaller one by saying, "Look, if I have defined a representation that works on the bigger one, then it'll also be a representation of the smaller one."

For example, this is a representation of the complex numbers, but if it's even graded, it just go to zero. But it's also a representation of the real numbers. But as a representation of the real numbers, it breaks up into two irreducible representations, so this is where you're looking at the quotient, you're saying, you had a {$2\times 2$} block and here also it's saying, there was only one representation, so this {$M(\textrm{Cl}_{0,k+1})$} is {$\mathbb{Z}$} because there's only one irreducible representation, and it can get be repeated arbitrarily many times to get reducible representations. But when you map {$M(\textrm{Cl}_{0,k+1})$} into {$M(\textrm{Cl}_{0,k})$}, you'll be mapping two to one, so you get {$\mathbb{Z}/2\mathbb{Z}\cong\mathbb{Z}$}.

You see how elaborate this is. You have to know about Morita equivalence, you have to know about graded representations, you have to know about representations, you know an inclusion map and back and forth, but that's all just mathematical baggage. Really you could tell a high school student or anyone if they know {$2\times 2$} matrices. You can explain that this is what it is.

And there may be a simpler math. There probably is a simpler math. To do it you don't really need the real numbers to talk about this. You can probably just use {$\mathbb{Z}_2$}. The real numbers here are just like a canvas, a wrapper. They aren't relevant here anywhere.

1:10:15 Brings to mind the twosome for existence by which opposites coexist or all is the same.

So the point is to understand this, first of all, what is this really saying? But what you can see, you can start to see something like the twosome, where it's saying that "opposites coexist" or "it's all the same". So that type of distinction is already creeping in here very dramatically.

John: So, Andrius, I do I have to get to a meeting at work.

So then that's what I wanted to show you. Any last comments?

John: It's sort of coming into focus. I mean, to some degree, it's coming into greater focus. It seems like Bott periodicity can be explained on all these different tracks. Bott's original track, he explained in terms of embeddings of symmetric spaces. It can be explained in terms of Clifford algebras. Am I correct here? And then you're saying that there are simple cases where you can see the Bott periodicity kind of emerging in that case of the breakdown of the complex numbers.

1:11:20 Explicit representations (matrices) and implicit structure (complex, quaternion) are separately expressed and related by the pattern.

All the cases are that simple. In conclusion, when you build up the Clifford algebras, the two building blocks are {$2\times 2$} real matrices by which you're tensoring and the quaternions by which you're tensoring.

It's like what you, John, have said about the complex numbers. You have this choice, you can define by fiat, saying I have an imaginary number {$i$}, or you can construct it, ending up with {$2\times 2$} matrices. You can do it either way and so this is like explicit representation or implicit structure.

If you go the route of implicit structure you get these {$\mathbb{Z}_2$}'s, you get {$\mathbb{R}$} to {$\mathbb{C}$} to {$\mathbb{H}$}. But if you keep going that route in the end you collapse back into this external perspective where it's saying you end up using matrices. When you use matrices, the quaternions are very sparse, in {$4\times 4$} matrices. Then you use the same size matrices understood as complex numbers, and then you use the same size matrices with real numbers where they fill up the space. So all the space that was sparse gets filled back up. So these matrices don't grow in size, which is why get the {$0$}'s, the trivial groups.

The conclusion is that something very simple is going on. It has very deep consequences in all these deep things in mathematics. It's related to the symmetry inherent in math itself, like how can you fold up a matrix. How does internal structure and external representation relate? So if we could understand it simply from a math point of view, in the way a high school or community college kid could understand, then that's the level that would relate to the Wondrous Wisdom. But already the twosome creeps in, the three-cycle creeps in.

And just to say a prayer of thanks.

Original content by Andrius Kulikauskas and Math 4 Wisdom are in the Public Domain for you and all to share, use and reuse in your own best judgment. I, Andrius Kulikauskas, certify my fair use of Wikipedia in this video. Authors of Wikipedia, thank you!

Thank you

Thank you for leaving comments, for liking this video and for subscribing to the Math 4 Wisdom YouTube channel!

Thank you Daniel Friedman, Kevin Armengol, John Harland, Bill Pahl and all for your support through Patreon! https://www.patreon.com/math4wisdom

Join our Math4Wisdom discussion group.

Visit http://www.math4wisdom.com to contact me, Andrius Kulikauskas, and learn more about Math4Wisdom!